２次関数のグラフ

2018.06.012020.06.09

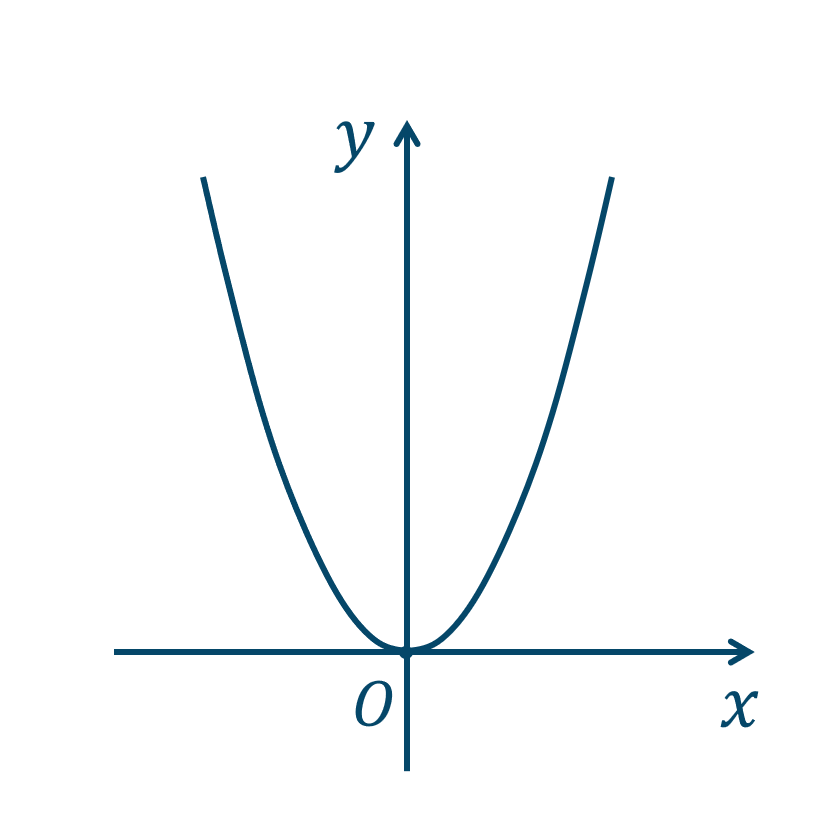
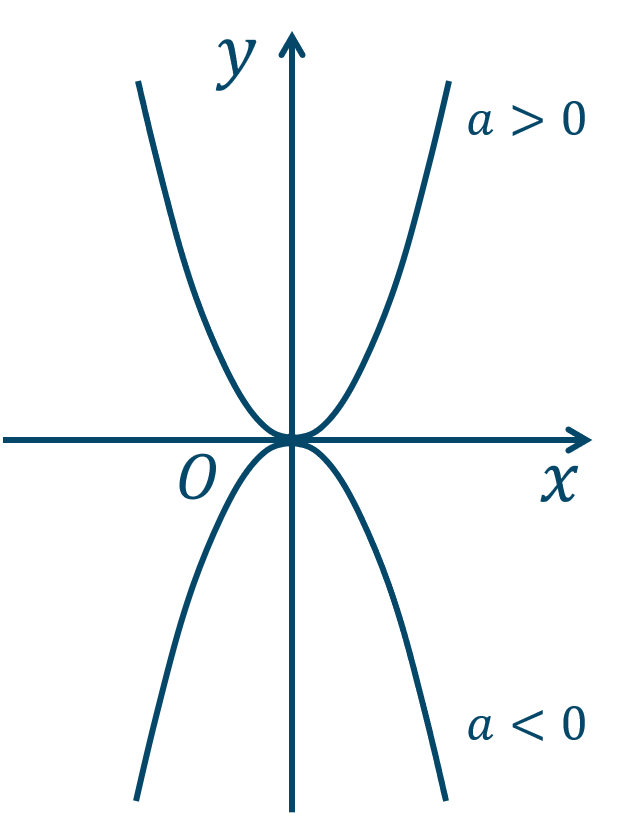
Point：２次関数のグラフ① $y=ax^2$ のグラフ
頂点は $(0,0)$、軸は直線 $x=0$ となります。
$a>0$ のときは下に凸
$a<0$ のときは上に凸
の放物線となります。

② $y=a(x-p)^2$ のグラフ
$y=ax^2$ のグラフを $x$ 軸方向に $+p$ 平行移動した放物線のグラフとなります。
頂点は $(p,0)$、軸は直線 $x=p$ となり、

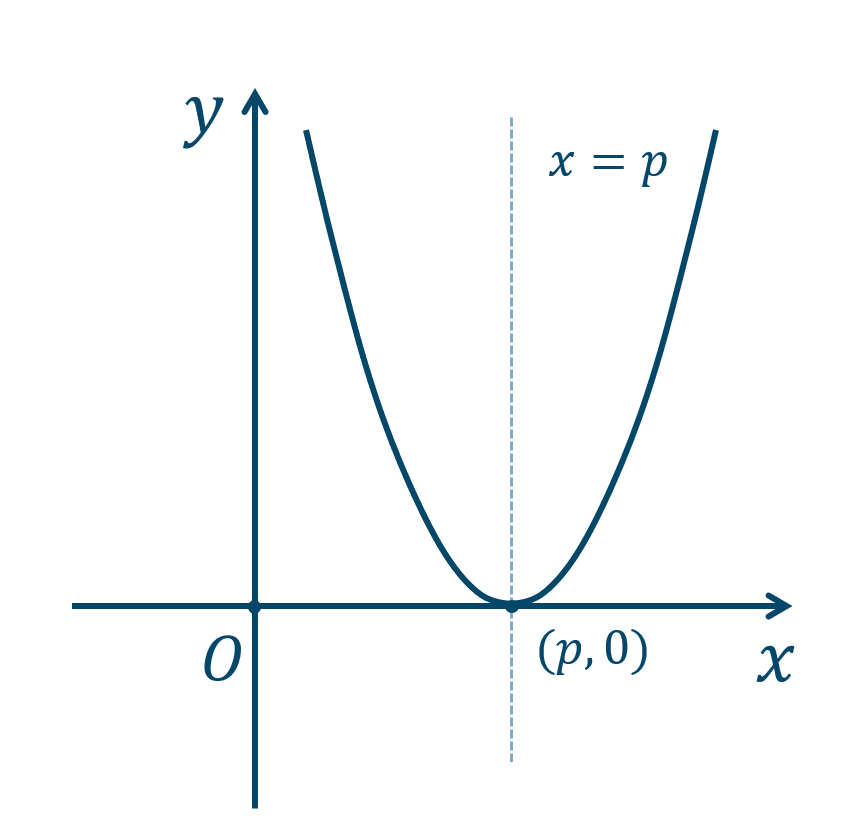
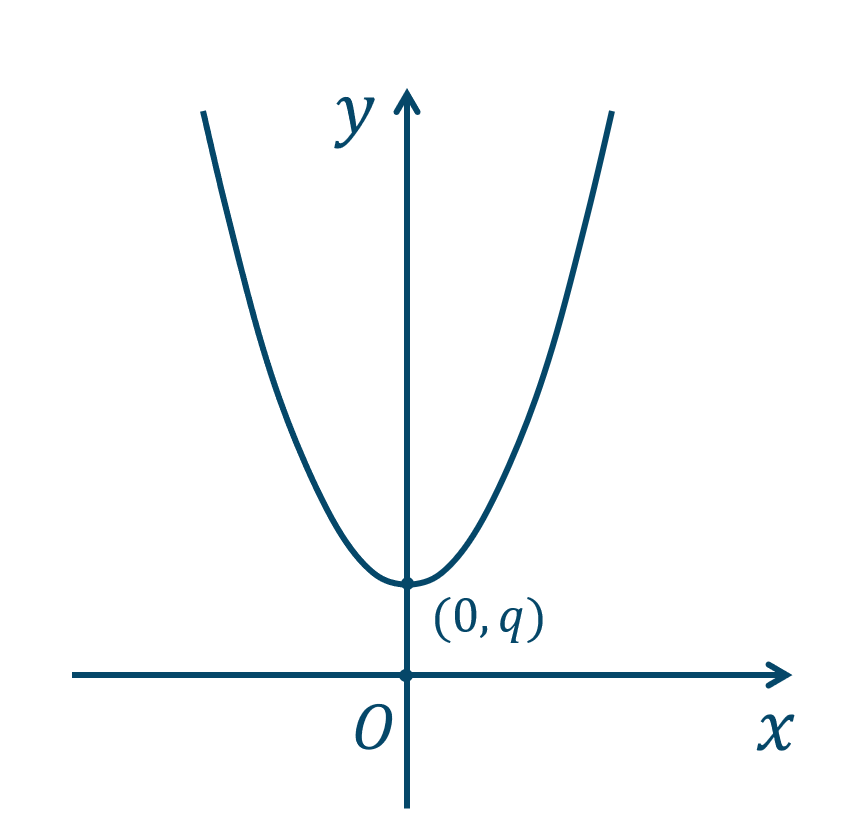
③ $y=ax^2+q$ のグラフ
$y=ax^2$ のグラフを $y$ 軸方向に $+q$ 平行移動した放物線のグラフとなります。
頂点は $(0,q)$、軸は直線 $x=0$ となり、

④ $y=a(x-p)^2+q$ のグラフ
$y=ax^2$ のグラフを $x$ 軸方向に $+p$、$y$ 軸方向に $+q$ 平行移動した放物線のグラフとなります。
頂点は $(p,q)$、軸は直線 $x=p$ となり、

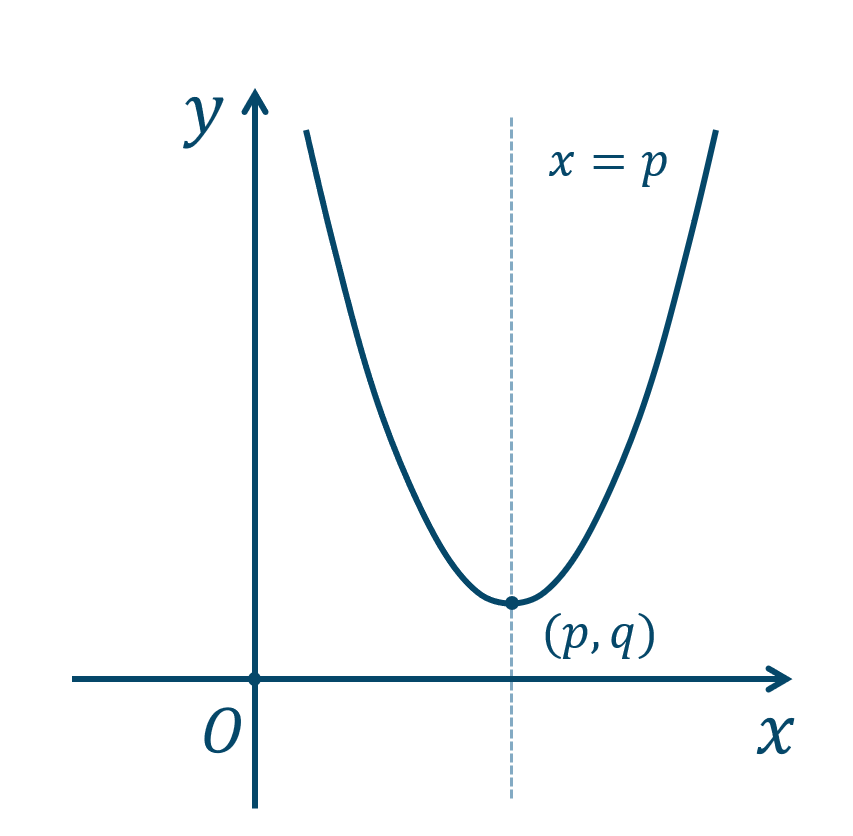
問題解説：２次関数のグラフ

問題次の関数のグラフをかけ。$${\small (1)}~y=2x^2$$

頂点 $(0,0)$、軸は直線 $x=0$ となるので、

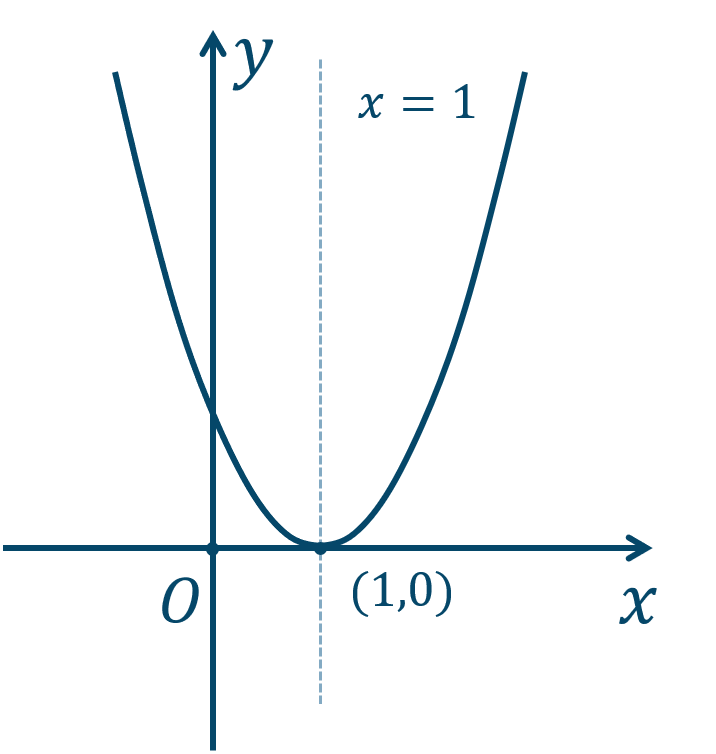
問題次の関数のグラフをかけ。$${\small (2)}~y=2(x-1)^2$$

頂点 $(1,0)$、軸は直線 $x=1$ となるので、

問題次の関数のグラフをかけ。$${\small (3)}~y=2x^2-3$$

頂点 $(0,-3)$、軸は直線 $x=0$ となるので、

問題次の関数のグラフをかけ。$${\small (4)}~y=2(x-1)^2-3$$

頂点 $(1,-3)$、軸は直線 $x=1$ となるので、

それぞれのパターンでグラフを描けるように練習しておきましょう。また、頂点や軸も求められるようになりましょう。