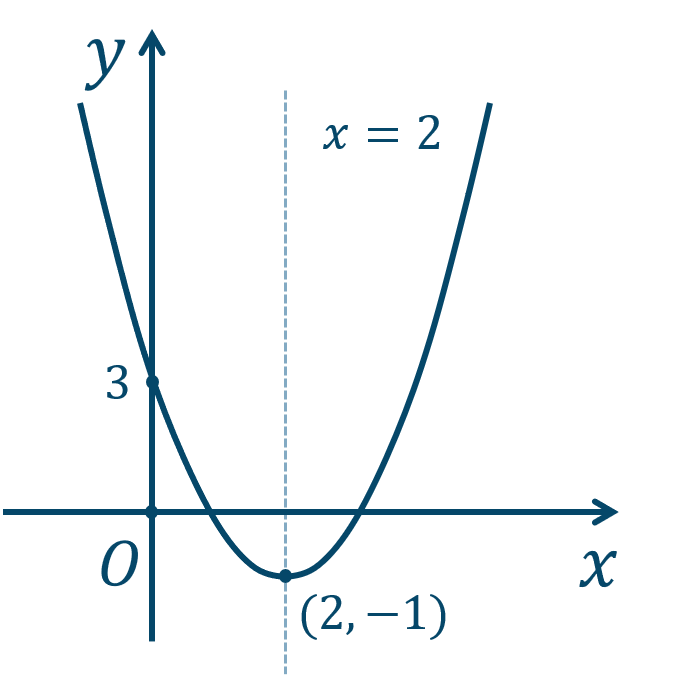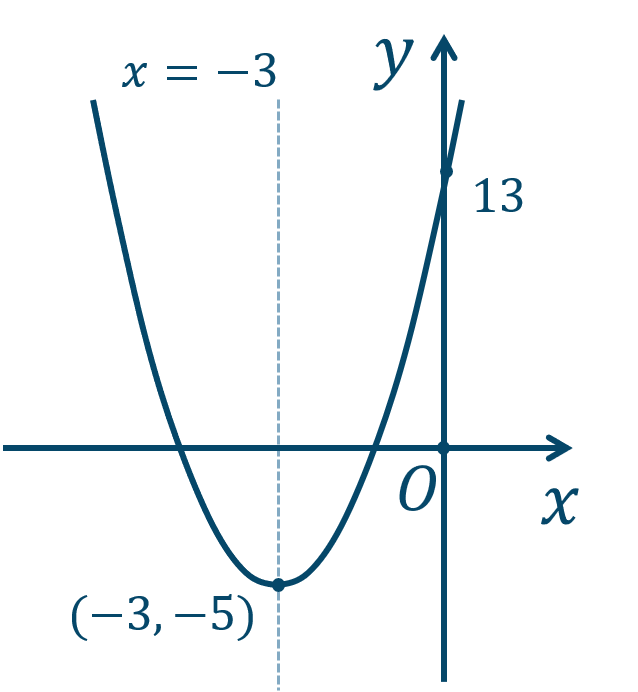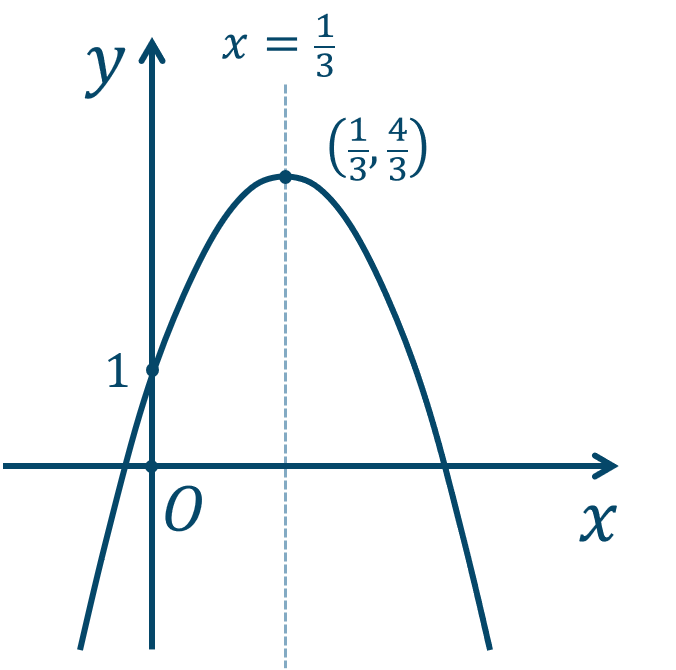2次関数の平方完成の解法
解法の手順は、
① \(x^2\) の係数で \(x^2\) と \(x\) の項をくくります。
② くくったあとの \(x\) の係数の値の「半分の2乗」を加えて引きます。
③ 引いた数はカッコの外に出します。このとき、カッコの係数をかけるのを忘れないようにしましょう。
④ カッコの中を因数分解して、後半部分を計算します。
\(y=ax^2+bx+c\) のグラフは、平方完成した式が \(y=a(x-p)^2+q\) のとき、
(1) \(a\) の値より、
\(a>0\) で下に凸のグラフ
\(a<0\) で上に凸のグラフ
(2) \(c\) の値は \(y\) 切片となります。
(3) 平方完成後の式より、
頂点 \((p,q)\)、軸 \(x=p\) となります。
問題解説:2次関数のグラフ
問題解説(1)
$$\hspace{ 10 pt}y=x^2-4x+3$$\(x\) の係数の値の半分の2乗である \(2^2\) を加えて引くと、$$\hspace{ 18 pt}=x^2-4x+2^2-2^2+3$$前半部分を因数分解すると、$$\hspace{ 18 pt}=(x-2)^2-2^2+3$$$$\hspace{ 18 pt}=(x-2)^2-4+3$$$$\hspace{ 18 pt}=(x-2)^2-1$$よって、頂点 \((2,-1)\)、軸が直線 \(x=2\) となります。
また、下に凸のグラフで \(y\) 切片が \(3\) となり、グラフは次のようになります。
問題解説(2)
$$\hspace{ 10 pt}y=2x^2+12x+13$$\(x^2\) と \(x\) の項をくくると、$$\hspace{ 18 pt}=2(x^2+6x)+13$$\(x\) 係数の値の半分の2乗である \(3^2\) を加えて引くと、$$\hspace{ 18 pt}=2(x^2+6x+3^2-3^2)+13$$引いた値をカッコの外に出すと、$$\hspace{ 18 pt}=2(x^2+6x+3^2)-2\cdot3^2+13$$カッコの中を因数分解し、後半部分は計算すると、$$\hspace{ 18 pt}=2(x+3)^2-18+13$$$$\hspace{ 18 pt}=2(x+3)^2-5$$よって、頂点 \((-3,-5)\)、軸が直線 \(x=-3\) となります。
また、下に凸のグラフで \(y\) 切片が \(13\) となり、グラフは次のようになります。
問題解説(3)
$$\hspace{ 10 pt}y=-3x^2+2x+1$$\(x^2\) と \(x\) の項をくくると、$$\hspace{ 18 pt}=-3\left( x^2-\frac{2}{3}x \right) +1$$\(x\) 係数の値の半分の2乗である \(\left({\Large \frac{1}{3}}\right)^2\) を加えて引くと、$$\hspace{ 18 pt}=-3\left\{ x^2 -\frac{2}{3}x+\left( \frac{1}{3} \right)^2-\left( \frac{1}{3} \right)^2 \right\}+1$$引いた値をカッコの外に出すと、$$\hspace{ 18 pt}=-3\left\{ x^2 -\frac{2}{3}x+\left( \frac{1}{3} \right)^2 \right\}$$$$\hspace{ 80 pt}-(-3)\cdot \left( \frac{1}{3} \right)^2+1$$カッコの中を因数分解し、後半部分は計算すると、$$\hspace{ 18 pt}=-3 \left( x-\frac{1}{3} \right) +\frac{1}{3}+1$$$$\hspace{ 18 pt}=-3 \left( x-\frac{1}{3} \right) +\frac{4}{3}$$よって、頂点と軸の直線は、$$~~~\left( \frac{1}{3},\frac{4}{3} \right)~~~,~~~x=\frac{1}{3}$$また、上に凸のグラフで \(y\) 切片が \(1\) となり、グラフは次のようになります。
今回のまとめ
平方完成はとても重要な計算となります。ここでしっかりと計算方法を覚えて練習しておきましょう。