2次関数のグラフの平行移動
① それぞれの2次関数を平方完成し、頂点を求めます。
② 移動前と移動後の頂点を比較して、どのように平行移動したかを求めます。
問題解説:2次関数のグラフの平行移動
平行移動後のグラフは$$\hspace{ 10 pt}y=2x^2+12x+20~~~\cdots{\large ①}$$平方完成すると、$$\hspace{ 18 pt}=2(x^2+6x)+20$$$$\hspace{ 18 pt}=2(x^2+6x+3^2-3^2)+20$$$$\hspace{ 18 pt}=2(x^2+6x+3^2)-2\cdot 3^2+20$$$$\hspace{ 18 pt}=2(x+3)^2-18+20$$$$\hspace{ 18 pt}=2(x+3)^2+2$$よって、頂点の座標は \((-3,2)\) となります。
平行移動前のグラフは、$$\hspace{ 10 pt}y=2x^2+4x-6~~~\cdots{\large ②}$$平方完成すると、$$\hspace{ 18 pt}=2(x^2+2x)-6$$$$\hspace{ 18 pt}=2(x^2+2x+1^2-1^2)-6$$$$\hspace{ 18 pt}=2(x^2+2x+1^2)-2\cdot 1^2-6$$$$\hspace{ 18 pt}=2(x+1)^2-2-6$$$$\hspace{ 18 pt}=2(x+1)^2-8$$よって、頂点の座標は \((-1,-8)\) となります。
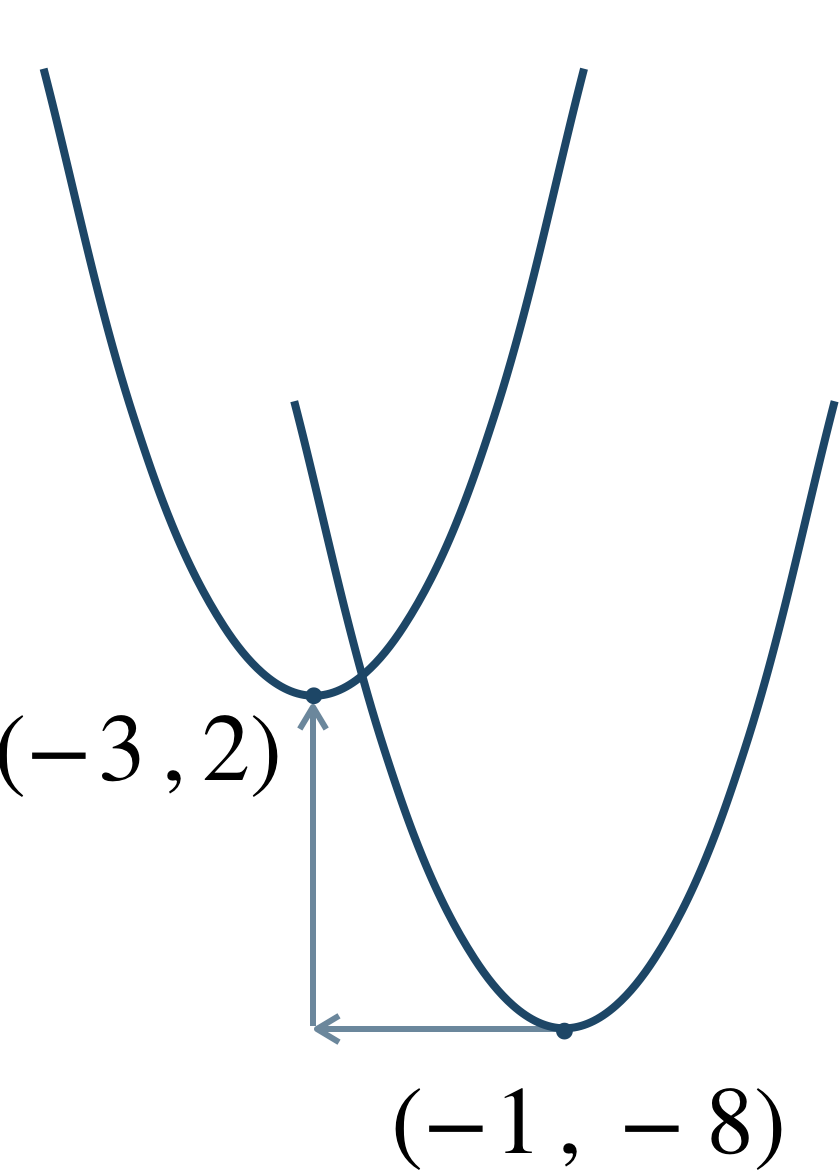
上のグラフより、②が①に平行移動するので \(x\) 座標の変化は、$$~~~-3-(-1)=-3+1=-2$$\(y\) 座標の変化は、$$~~~2-(-8)=10$$
よって、答えは \(x\) 軸方向に \(-2\)、\(y\) 軸方向に \(10\) だけ平行移動したことになります。
今回のまとめ
2次関数がどのように平行移動したかは、それぞれの頂点を求めて比較しましょう。計算するとき、引く順番に注意しましょう。