2次関数の最大値・最小値
② グラフを描きます。
このとき、\(y\) 軸はかかずに簡易的に描きましょう。また、\(x\) 軸の位置もグラフと交わらないように描きます。
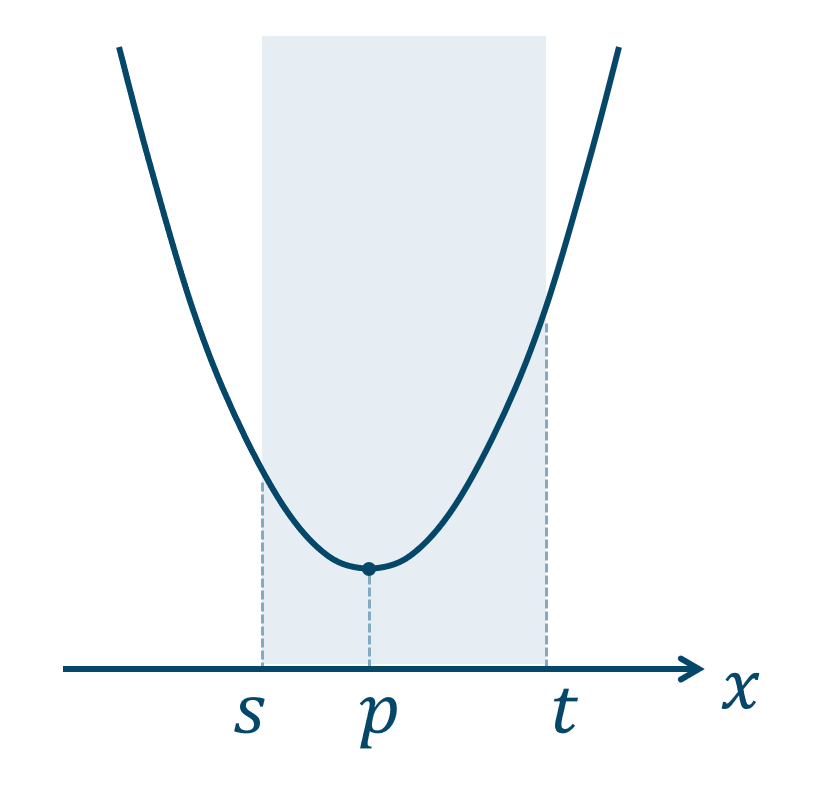
③ グラフより視覚的に最大値・最小値をとる \(x\) の値を求めます。その \(x\) の値のときの \(y\) の値が最大値・最小値となります。
上のグラフでは、
\(x=t\) のとき、最大値
\(x=p\) のとき、最小値
となります。
問題解説:2次関数の最大値・最小値
問題解説(1)
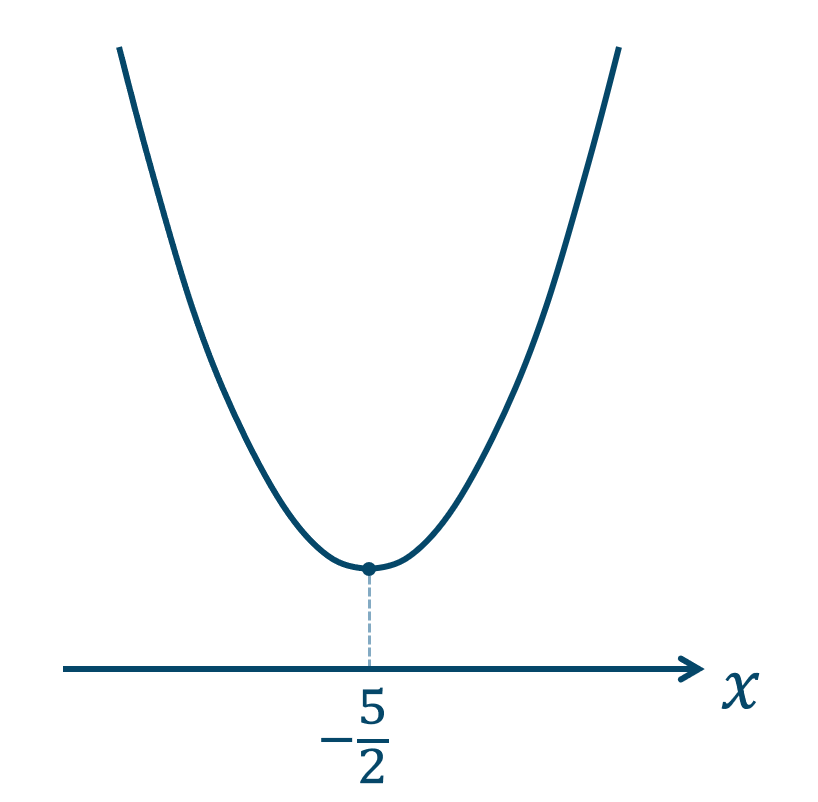
$$\hspace{ 10 pt}y=x^2+5x$$平方完成すると、$$\hspace{ 18 pt}=x^2+5x+\left(\frac{5}{2}\right)^2-\left(\frac{5}{2}\right)^2$$$$\hspace{ 18 pt}=\left(x+\frac{5}{2}\right)^2-\frac{25}{4}$$よって、頂点の座標は、$$~~~\left(-\frac{5}{2}~,~-\frac{25}{4}\right)$$となり、下に凸のグラフを簡易的に描くと、
よって、最大値はなく
\(x=-{\Large \frac{5}{2}}\) のとき最小値をとります。
\(x=-{\Large \frac{5}{2}}\) のとき、頂点の \(y\) 座標が最小値となり、$$~~~y=-\frac{25}{4}$$
よって、答えは、
最大値なし
最小値は、$$~~~-\frac{25}{4}~~~\left(x=-\frac{5}{2}\right)$$となります。
問題解説(2)
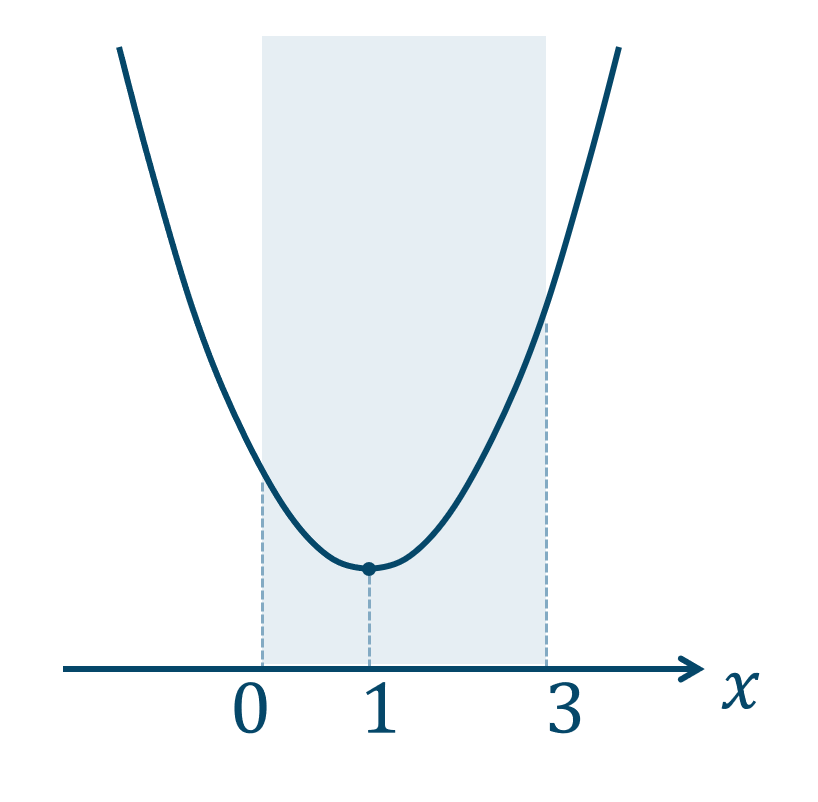
$$\hspace{ 10 pt}y=x^2-2x+6$$平方完成すると、$$\hspace{ 18 pt}=x^2-2x+1^2-1^2+6$$$$\hspace{ 18 pt}=(x-1)^2-1+6$$$$\hspace{ 18 pt}=(x-1)^2+5$$よって、頂点の座標は、$$~~~(1~,~5)$$となり、下に凸のグラフを簡易的に描くと、
よって、グラフより
\(x=3\) のとき、最大値となり
\(x=1\) のとき、最小値となります。
\(x=3\) のとき、\(y\) の値が最大値となるので、$$\hspace{ 10 pt}y=3^2-2\cdot3+6$$$$\hspace{ 18 pt}=9-6+6$$$$\hspace{ 18 pt}=9$$\(x=1\) のとき、頂点の \(y\) 座標が最小値となり、$$~~~y=5$$
したがって、答えは
最大値が$$~~~9~~~(x=3)$$最小値が$$~~~5~~~(x=1)$$となります。
問題解説(3)
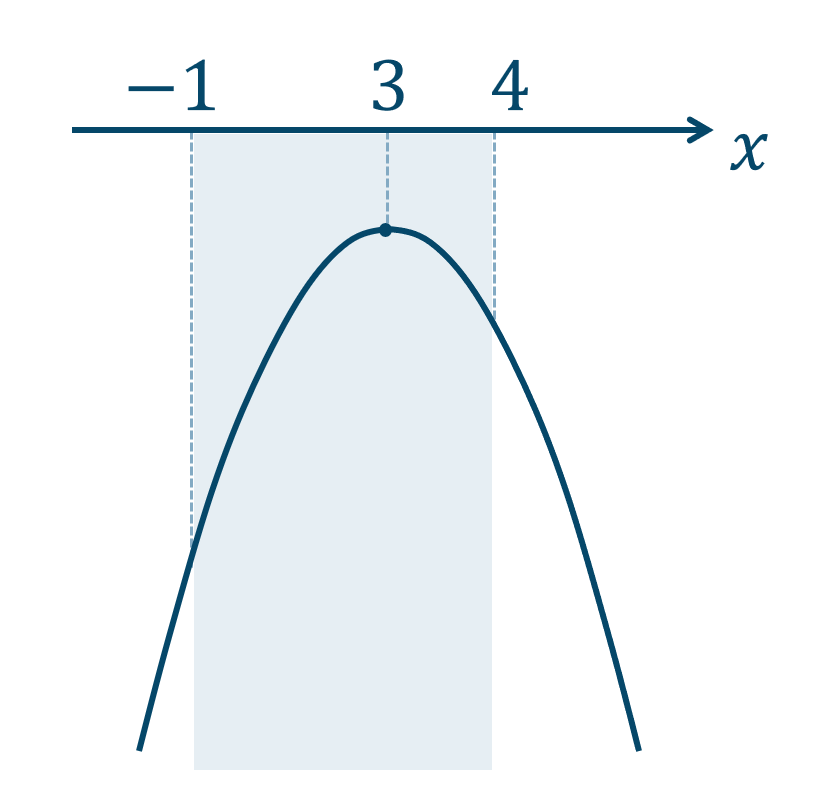
$$\hspace{ 10 pt}y=-x^2+6x-4$$平方完成すると、$$\hspace{ 18 pt}=-(x^2-6x)-4$$$$\hspace{ 18 pt}=-(x^2-6x+3^2-3^2)-4$$$$\hspace{ 18 pt}=-(x^2-6x+3^2)+3^2-4$$$$\hspace{ 18 pt}=-(x-3)^2+9-4$$$$\hspace{ 18 pt}=-(x-3)^2+5$$よって、頂点の座標が$$~~~(3~,~5)$$となり、上に凸のグラフを簡易的に描くと、
よって、グラフより
\(x=3\) のとき、最大値となり
\(x=-1\) のとき、最小値となります。
\(x=3\) のとき、頂点の \(y\) 座標が最大値となり、$$~~~y=5$$\(x=-1\) のとき、\(y\) の値が最小値となるので、$$\hspace{ 10 pt}y=-(-1)^2+6\cdot(-1)-4$$$$\hspace{ 18 pt}=-1-6-4$$$$\hspace{ 18 pt}=-11$$
したがって、答えは
最大値が$$~~~5~~~(x=3)$$最小値が$$~~~-11~~~(x=-1)$$となります。
今回のまとめ
2次関数の最大値・最小値の問題は、まずは与えられた2次関数を平方完成して、軸の方程式を求めましょう。軸の方程式と定義域より、グラフを簡易的に描いて最大値と最小値を視覚的に捉えましょう。