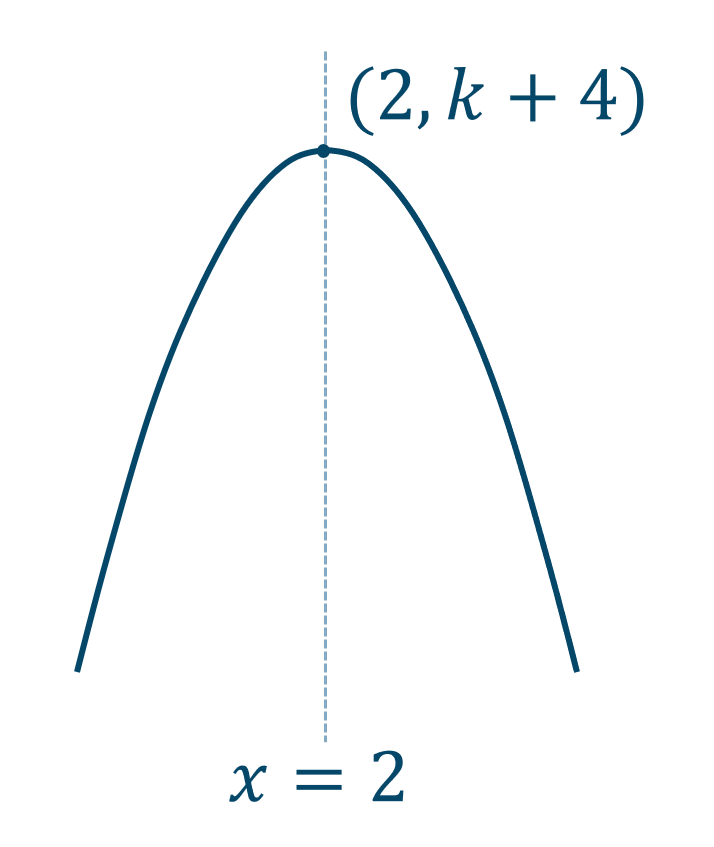2次関数の決定③(最大値・最小値)
② グラフより、
最大値とそのときの \(x\) の値
最小値とそのときの \(x\) の値
をそれぞれ読み取ります。
③ 読み取った \((x~,~y)\) の値を2次関数に代入して条件式とします。
④ 条件式より、未知数を求めて2次関数を決定します。
問題解説:2次関数の決定③(最大値・最小値)
問題解説(1)
\({\small (1)}\) 次の2次関数の最大値が \(5\) のとき、\(k\) の値を求めよ。$$~~~y=-x^2+4x+k$$
2次関数を平方完成すると、$$\hspace{ 10 pt}y=-x^2+4x+k$$$$\hspace{ 18 pt}=-(x^2-4x)+k$$$$\hspace{ 18 pt}=-(x^2-4x+2^2-2^2)+k$$$$\hspace{ 18 pt}=-(x^2-4x+2^2)+2^2+k$$$$\hspace{ 18 pt}=-(x-2)^2+k+4$$よって、頂点の座標が$$~~~(2~,~k+4)$$となり、上に凸のグラフとなるので、次のようになります。
グラフより、\(x=2\) のとき最大値をとるので、頂点の \(y\) 座標である \(k+4\) が最大値となります。
また、問題より最大値は \(5\) であるので、$$\hspace{ 10 pt}k+4=5$$移項すると、$$\hspace{ 10 pt}k=5-4$$$$\hspace{ 10 pt}k=1$$よって、求める2次関数は、$$~~~y=-x^2+4x+1$$となります。
問題解説(2)
\({\small (2)}\) 次の2次関数の最大値が \(3\) のとき、\(k\) の値とこの関数の最小値を求めよ。$$~~~y=x^2+2x+k~~~(-2≦x≦2)$$
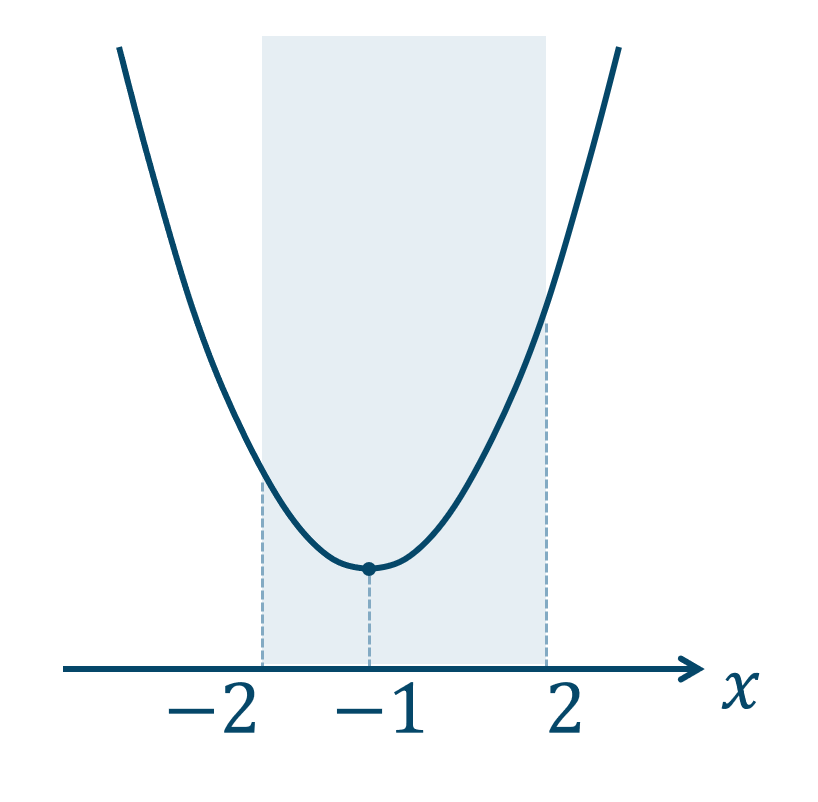
2次関数を平方完成すると、$$\hspace{ 10 pt}y=x^2+2x+k$$$$\hspace{ 18 pt}=x^2+2x+1^2-1^2+k$$$$\hspace{ 18 pt}=(x+1)^2+k-1$$よって、頂点の座標が$$~~~(-1~,~k-1)$$となり、下に凸のグラフとなるので、次のようになります。
グラフより、
\(x=2\) のとき最大値となり、
\(x=-1\) のとき最小値となります。
\(x=2\) のとき、最大値は \(y\) 座標より、$$\hspace{ 10 pt}y=2^2+2\cdot2+k$$$$\hspace{ 18 pt}=4+4+k$$$$\hspace{ 18 pt}=k+8$$また、問題文より最大値が \(3\) となるので、$$\hspace{ 10 pt}k+8=3$$移項すると、$$\hspace{ 10 pt}k=3-8$$$$\hspace{ 10 pt}k=-5$$
次に、\(x=-1\) のとき、頂点の \(y\) 座標の \(k-1\) が最小値となり、上の \(k\) の値を代入すると、$$~~~(-5)-1=-6$$
したがって答えは、$$~~~k=-5$$最小値は、$$~~~-6~~~(x=-1)$$となります。
今回のまとめ
2次関数の決定で最大値・最小値が条件のときは、そのグラフを描いて最大値・最小値をとる \(x\) の値を視覚的に求めて条件式にしましょう。