最大値・最小値の文章問題
① 図形についての問題のときは、条件に合う図形を描いて考えましょう。
② 変数は複数にならないように、工夫して \(x\) と置きます。
③ 図形より、2次関数の式を作り最大値・最小値を求めます。
問題解説:最大値・最小値の文章問題
問題解説(1)
\({\small (1)}\) この針金で長方形を作り面積を最大にするとき、その面積の最大値を求めよ。
\(12\) cmの針金で長方形を作るとき、周りの長さが \(12\) cmとなるので、縦+横の長さはその半分の \(6\) cmとなります。
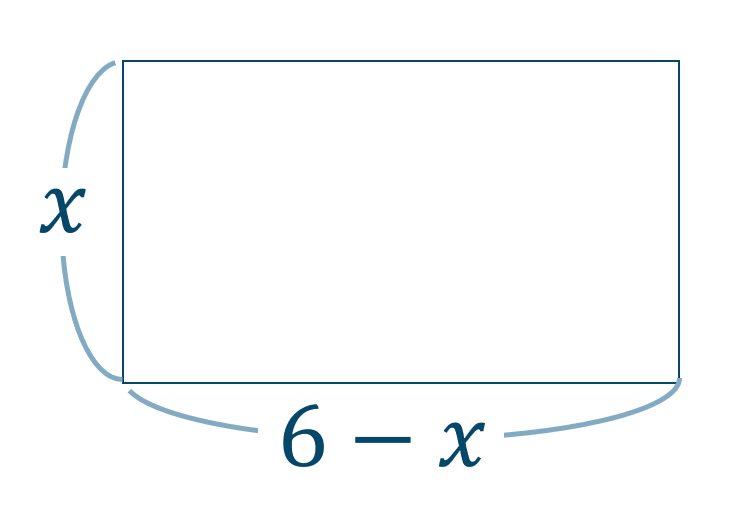
縦の長さを \(x\) と置くと、横の長さは \(6-x\) となるので、図形は次のようになります。
また、辺の長さとなることより、$$~~~x>0~,~6-x>0$$\(6-x>0\) より、$$\hspace{ 10 pt}6-x>0$$移項すると、$$\hspace{ 10 pt}-x>-6$$両辺に \(-1\) をかけると、不等号の向きが逆になるので、$$\hspace{ 16 pt}x<6$$よって、\(x>0\) と合わせると、\(0 < x < 6\) となります。
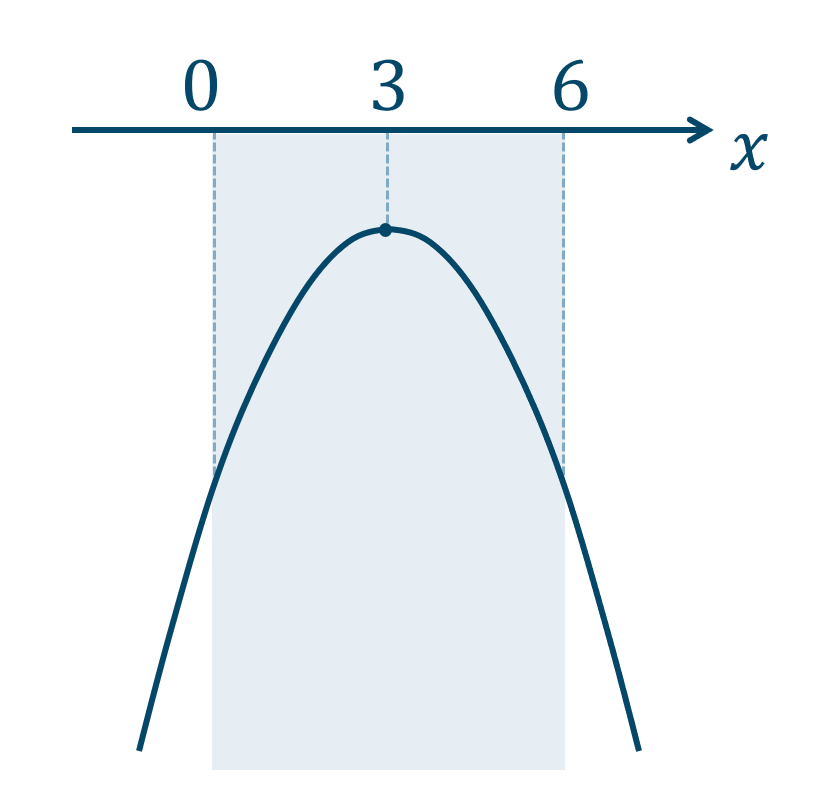
次に長方形の面積を \(y\) とすると、$$\hspace{ 10 pt}y=x(6-x)$$$$\hspace{ 18 pt}=6x-x^2$$$$\hspace{ 18 pt}=-x-2+6x$$平方完成すると、$$\hspace{ 18 pt}=-(x^2-6x)$$$$\hspace{ 18 pt}=-(x^2-6x+3^2-3^2)$$$$\hspace{ 18 pt}=-(x^2-6x+3^2)+3^2$$$$\hspace{ 18 pt}=-(x-3)^2+9$$よって、頂点の座標が$$~~~(3~,~9)$$となり、上に凸のグラフは次のようになります。
グラフより、\(0 < x < 6\) の範囲で、
\(x=3\) のとき、最大値 \(9\) をとります。
よって、答えは、面積の最大値 \(9\) となります。
問題解説(2)
\({\small (2)}\) この針金を2つに分けて、2つの正方形を作る。このとき、2つの正方形の面積の和を最小にするにはどのように針金を分ければよいか答えよ。
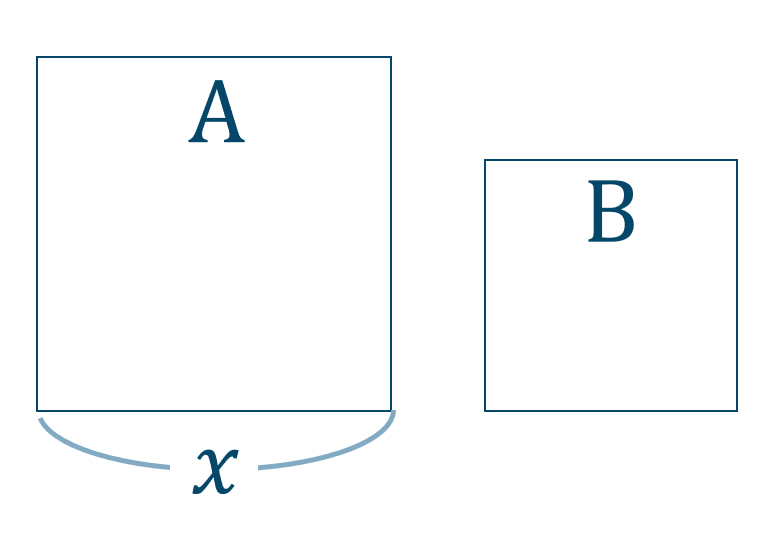
Aの一辺の長さを \(x\) cmとすると、周りの長さは \(4x\) cmとなります。
また、Bの周りの長さは針金の長さが \(12\) cmで2つに分けていることより、\(12-4x\) cmとなります。
これより、Bの一辺の長さは、$$~~~\frac{12-4x}{4}=3-x$$よって、\(3-x\) cmとなります。
また、それぞれ辺の長さであることより、$$~~~x>0~,~3-x>0$$\(3-x>0\) より、$$\hspace{ 10 pt}3-x>0$$移項すると、$$\hspace{ 10 pt}-x>-3$$両辺に \(-1\) をかけると、不等号の向きが逆になるので、$$\hspace{ 16 pt}x<3$$よって、\(x>0\) と合わせると、\(0 < x < 3\) となります。
次に、Aの正方形の面積は、\(x^2\)
Bの正方形の面積は、\((3-x)^2\)
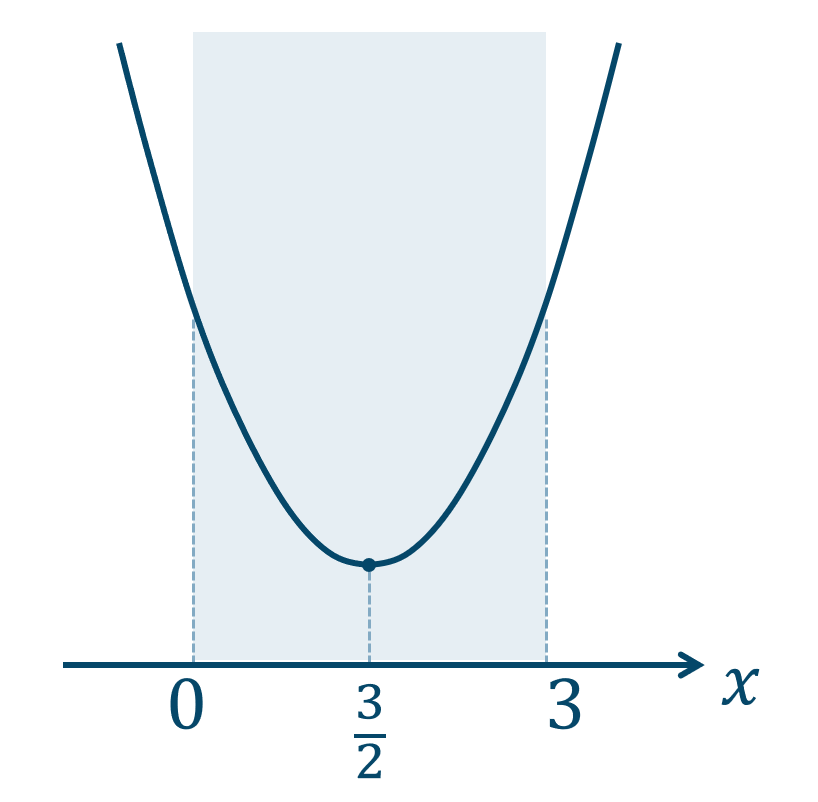
2つの正方形の面積の和を \(y\) とすると、$$\hspace{ 10 pt}y=x^2+(3-x)^2$$$$\hspace{ 18 pt}=x^2+9-6x+x^2$$$$\hspace{ 18 pt}=2x^2-6x+9$$平方完成すると、$$\hspace{ 18 pt}=2(x^2-3x)+9$$$$\hspace{ 18 pt}=2\left(x^2-3x+\frac{9}{4}-\frac{9}{4}\right)+9$$$$\hspace{ 18 pt} =2\left(x^2-3x+\frac{9}{4}\right)-2\cdot\frac{9}{4}+9$$$$\hspace{ 18 pt}=2\left(x-\frac{3}{2}\right)^2-\frac{9}{2}+9$$$$\hspace{ 18 pt}=2\left(x-\frac{3}{2}\right)^2+\frac{-9+18}{2}$$$$\hspace{ 18 pt}=2\left(x-\frac{3}{2}\right)^2+\frac{9}{2}$$よって、頂点の座標が$$~~~\left(\frac{3}{2}~,~\frac{9}{2}\right)$$となり、下に凸のグラフは次のようになります。
グラフより、\(0 < x < 3\) の範囲で、
\(x={\Large \frac{3}{2}}\) のとき、最小値となります。
これより、Aの一辺の長さを \({\Large \frac{3}{2}}\) cmとすればよいので、周りの長さは、$$~~~4\cdot\frac{3}{2}=6$$よって、\(6\) cmとなります。
また、Bの周りの長さは、$$~~~12-6=6$$よって、\(6\) cmとなります。
したがって、答えは、
針金を \(6\) cmずつに分ければよい
となります。
今回のまとめ
図形を描いて変数が複数にならないように、何を \(x\) とするかを工夫しましょう。また、置いた文字の範囲にも注意して問題を解いていきましょう。