放物線と直線の交点の求め方
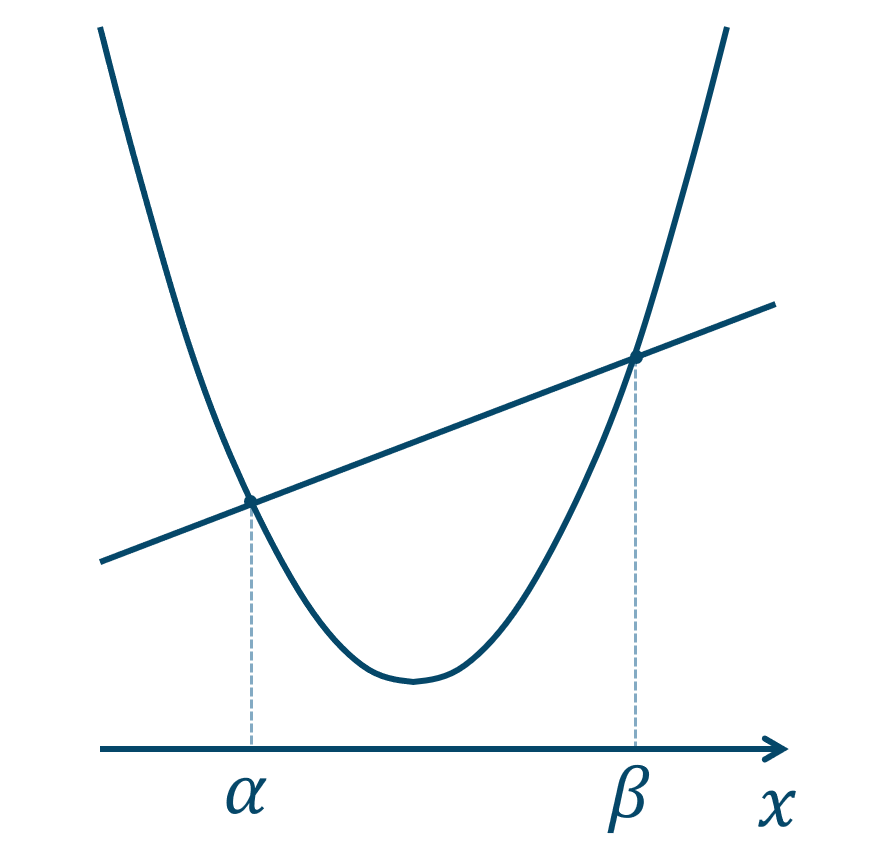$$~~~\biggl\{ \begin{eqnarray} y=ax^2+bx+c \\ y=mx+n \end{eqnarray}$$２次関数の式と直線の式を連立した２次方程式を解くと、交点の \(x\) 座標を求めることができます。また、交点の個数は、連立した２次方程式の判別式 \(D\) を用いて判別できます。
( ⅰ ) \(D>0\) のとき
２次方程式の解が２個となるので、この２次関数と直線は２点で交わります。
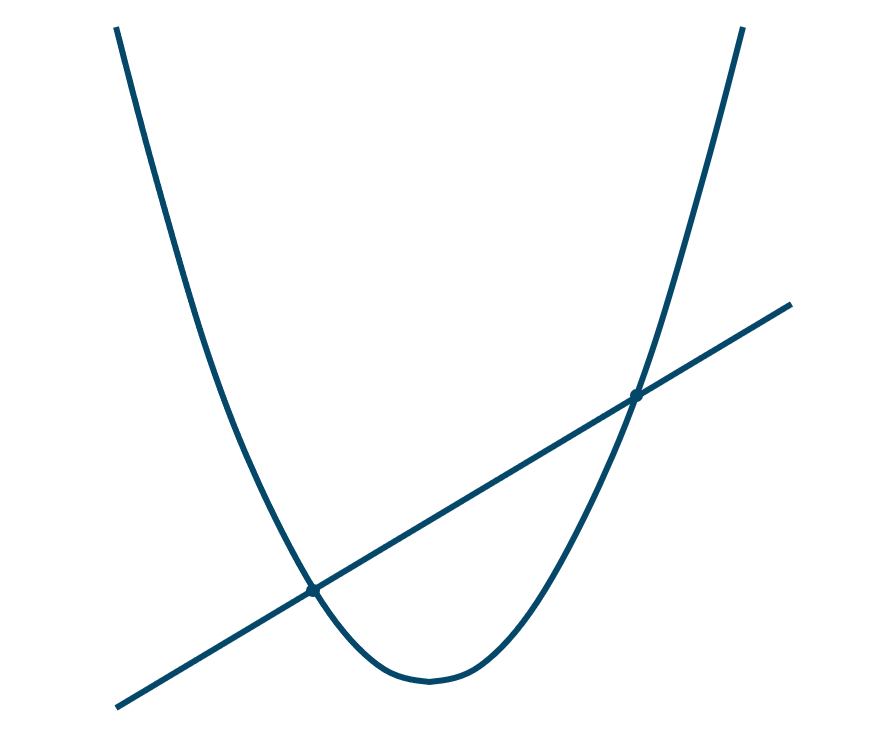
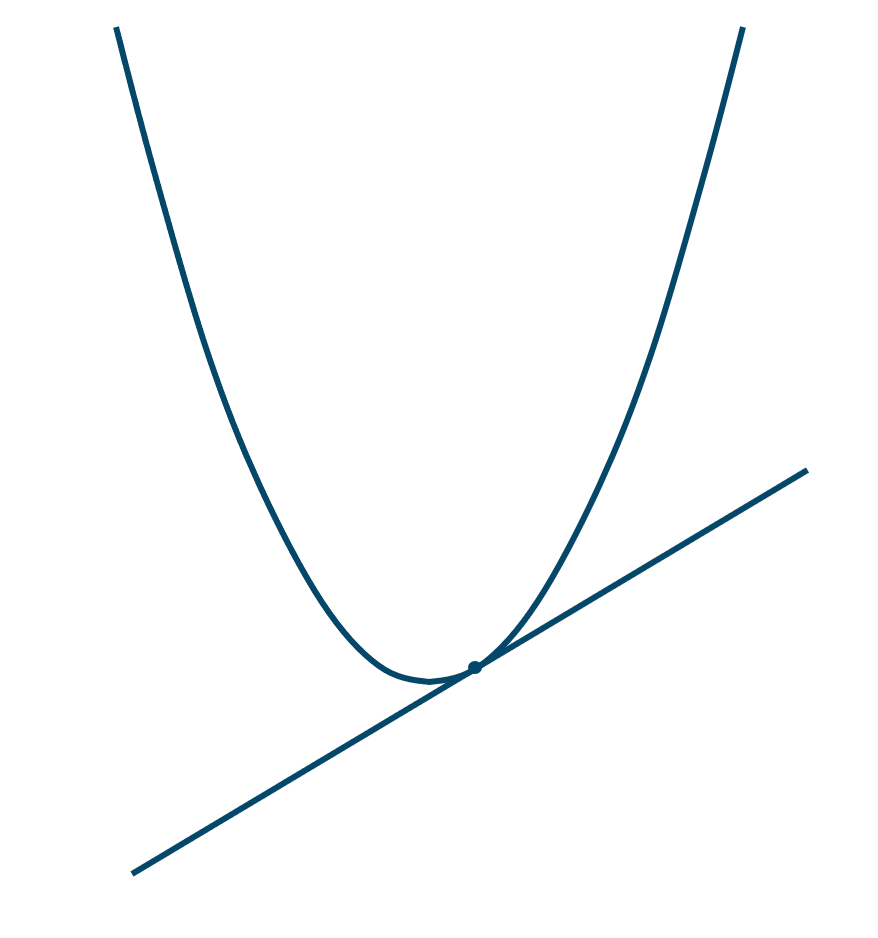
( ⅱ ) \(D=0\) のとき
２次方程式の解が１個(重解)となるので、この２次関数と直線は接します。(交点が１個)
( ⅲ ) \(D<0\) のとき
２次方程式の解なしとなるので、この２次関数と直線との交点なしとなります。
問題解説：放物線と直線の交点
問題解説(1)
\({\small (1)}\) 次の放物線と直線との交点の座標を求めよ。$$~~~\biggl\{ \begin{eqnarray} y=x^2+5x-5 \\ y=2x+5 \end{eqnarray}$$
$$\hspace{ 10 pt}\biggl\{ \begin{eqnarray} y=x^2+5x-5~\cdots{\large ①} \\ y=2x+5 ~\cdots{\large ②}\end{eqnarray}$$この２つの式より、\(y\) を消去すると、$$\hspace{ 10 pt}x^2+5x-5=2x+5$$移項すると、$$\hspace{ 10 pt}x^2+5x-5-2x-5=0$$$$\hspace{ 46 pt}x^2+3x-10=0$$左辺を因数分解すると、$$\hspace{ 10 pt}(x+5)(x-2)=0$$$$\hspace{ 50 pt}x=-5~,~2$$
\(x=-5\) のとき、②の式より、$$\hspace{ 10 pt}y=2\cdot(-5)+5$$$$\hspace{ 18 pt}=-10+5$$$$\hspace{ 18 pt}=-5$$よって、座標は$$~~~(-5~,~-5)$$
また、\(x=2\) のとき、②の式より、$$\hspace{ 10 pt}y=2\cdot 2+5$$$$\hspace{ 18 pt}=4+5$$$$\hspace{ 18 pt}=9$$よって、座標は$$~~~(2~,~9)$$
以上より、求める交点の座標は、$$~~~(-5~,~-5)~,~(2~,~9)$$となります。
問題解説(2)
\({\small (2)}\) 次の放物線と直線が接するとき、\(k\) の値と接点の座標を求めよ。$$~~~\biggl\{ \begin{eqnarray} y=x^2+5x-5 \\ y=x-k \end{eqnarray}$$
$$\hspace{ 10 pt}\biggl\{ \begin{eqnarray} y=x^2+5x-5~\cdots{\large ①} \\ y=x-k~\cdots{\large ②} \end{eqnarray}$$この２つの式より、\(y\) を消去すると、$$\hspace{ 10 pt}x^2+5x-5=x-k$$移項すると、$$\hspace{ 10 pt}x^2+5x-5-x+k=0$$$$\hspace{ 28 pt}x^2+4x+k-5=0~\cdots{\Large ③}$$
①と②が接するとき、この２次方程式の解が重解をもつときとなるので、判別式 \(D\) を考えると、$$\hspace{ 10 pt}D=4^2-4\cdot1\cdot(k-5)$$$$\hspace{ 20 pt}=16-4(k-5)$$$$\hspace{ 20 pt}=16-4k+20$$$$\hspace{ 20 pt}=36-4k$$解が１つであるとき、\(D=0\) となるので、$$\hspace{ 10 pt}36-4k=0$$移項して、\(-4\) で割ると$$\hspace{ 10 pt}-4k=-36$$$$\hspace{ 22 pt}k=\frac{-36}{-4}$$$$\hspace{ 22 pt}k=9$$
また、接点の座標は③に \(k=9\) を代入することより$$\hspace{ 10 pt}x^2+4x+9-5=0$$$$\hspace{27 pt}x^2+4x+4=0$$左辺を因数分解すると、$$\hspace{ 10 pt}(x+2)^2=0$$\(x+2=0\) であることより、$$\hspace{ 10 pt}x+2=0$$$$\hspace{ 28 pt}x=-2$$次に、\(y\) 座標は②の式に \(x=-2\) と \(k=9\) を代入することより、$$\hspace{ 10 pt}y=-2-9$$$$\hspace{ 18 pt}=-11$$よって、座標は$$~~~(-2~,~-11)$$となります。
よって、答えは$$~~~k=9~,~(-2~,~-11)$$となります。
今回のまとめ
放物線と直線の交点についての問題は、２次関数と直線の方程式を連立した２次方程式の問題にすることを覚えておきましょう。
