2次不等式の解(因数分解)
① 左辺にすべての項をまとめて、\(x^2\) の係数が負の数のときは両辺に \(-1\) をかけて正の数とします。このとき、不等式の向きが逆になることに注意しましょう。
② 左辺を \((x-\alpha)(x-\beta)\) と因数分解します。
(1) \(ax^2+bx+c≧0\) のとき
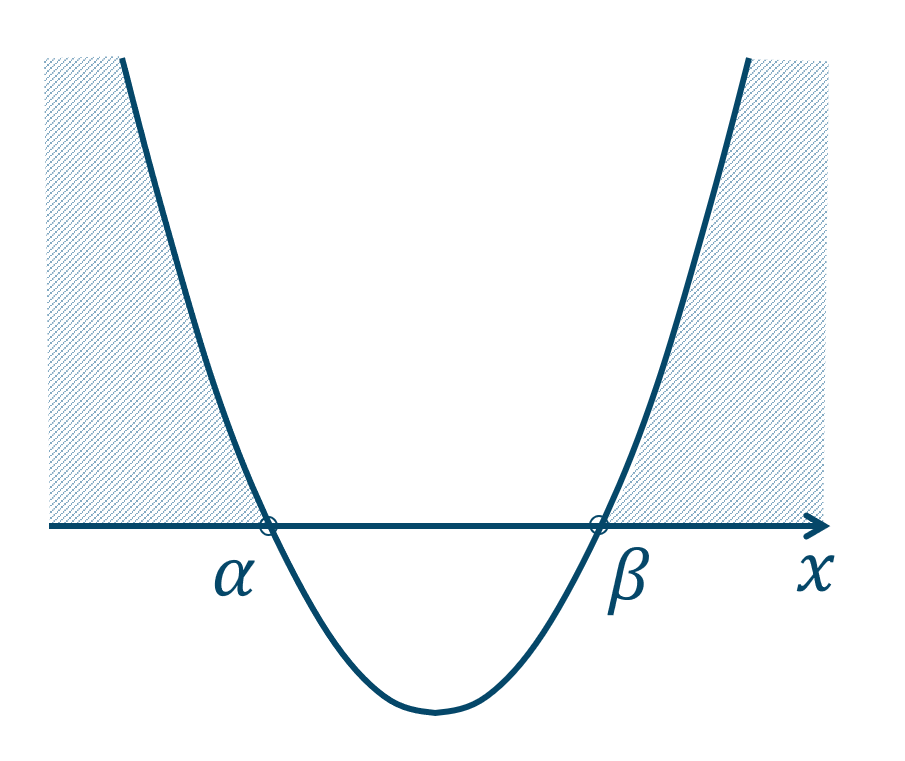
左辺が因数分解されて、$$~~~(x-\alpha)(x-\beta)≧0$$左辺を \(y\) としたグラフを描くと、
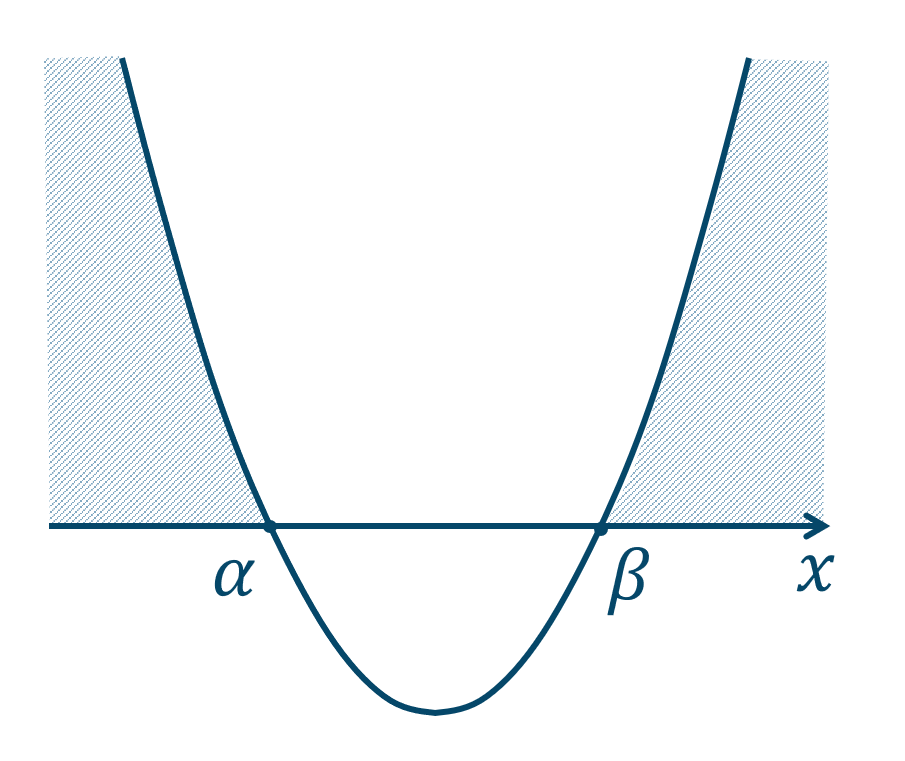
このグラフより、\(y≧0\) となる範囲が解となるので、
となります。
(2) \(ax^2+bx+c>0\) のとき
左辺が因数分解されて、$$~~~(x-\alpha)(x-\beta)>0$$左辺を \(y\) としたグラフを描くと、
このグラフより、\(y>0\) となる範囲が解となるので、
となります。
(3) \(ax^2+bx+c≦0\) のとき
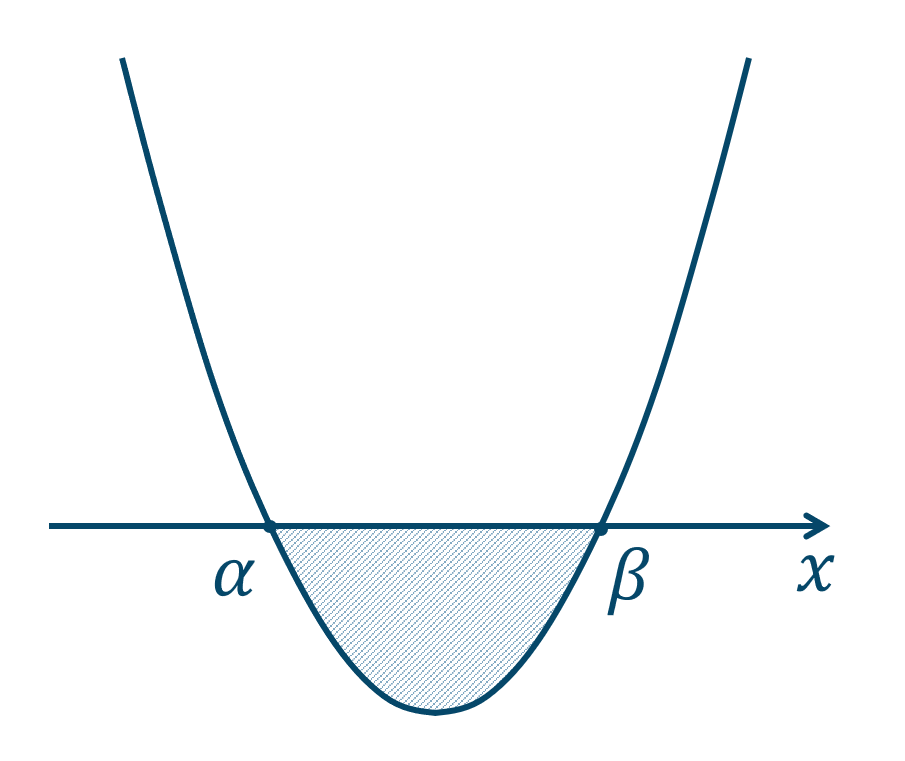
左辺が因数分解されて、$$~~~(x-\alpha)(x-\beta)≦0$$左辺を \(y\) としたグラフを描くと、
このグラフより、\(y≦0\) となる範囲が解となるので、
となります。
(4) \(ax^2+bx+c<0\) のとき
左辺が因数分解されて、$$~~~(x-\alpha)(x-\beta)<0$$左辺を \(y\) としたグラフを描くと、
このグラフより、\(y<0\) となる範囲が解となるので、
となります。
問題解説:2次不等式の解①(因数分解)
問題解説(1)
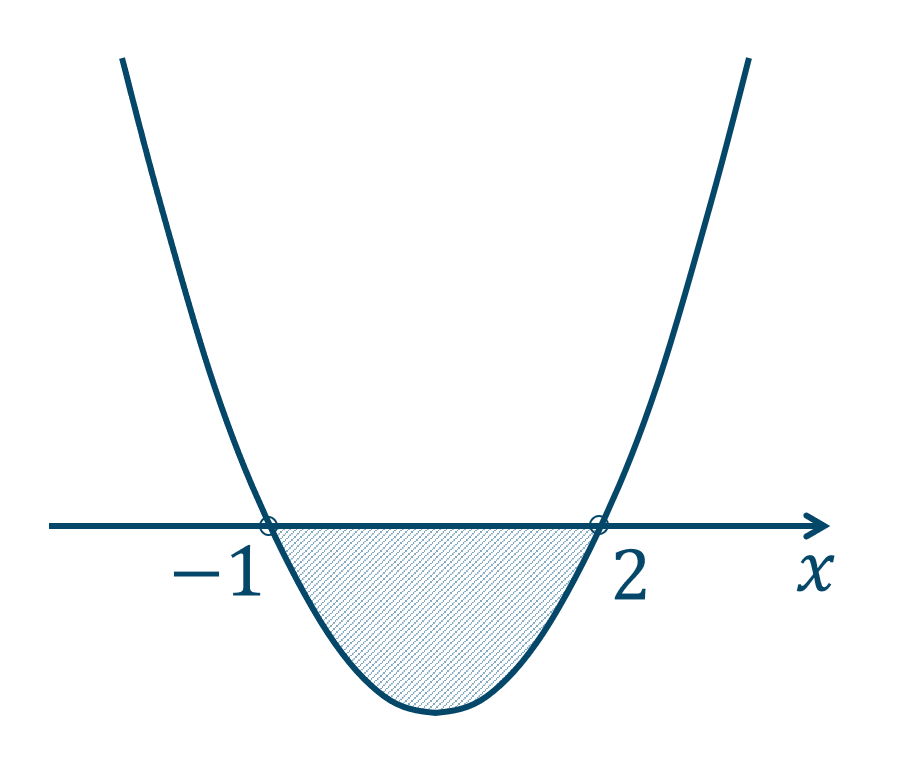
左辺を因数分解すると、$$\hspace{ 10 pt}(x+1)(x-2)<0$$ここで、左辺を \(y\) としたときのグラフは、\(x\) 軸と \(x=-1~,~2\) で交わるので、
このグラフより \(y<0\) となるような範囲が解となるので、答えは$$~~~-1<x<2$$となります。
問題解説(2)
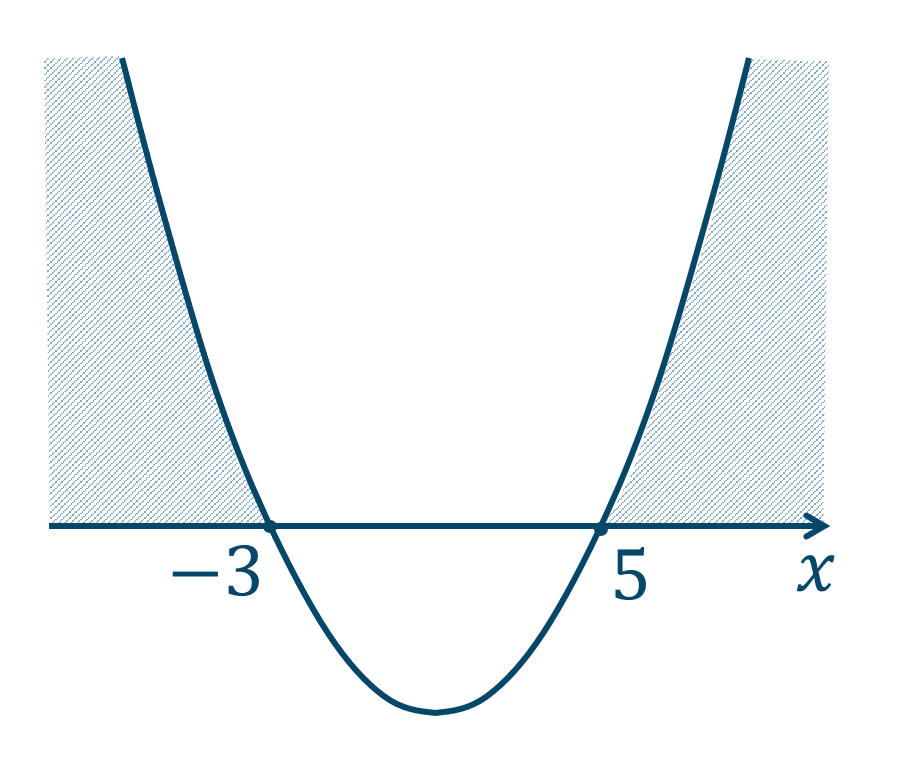
左辺を因数分解すると、$$\hspace{ 10 pt}(x+3)(x-5)≧0$$ここで、左辺を \(y\) としたときのグラフは、\(x\) 軸と \(x=-3~,~5\) で交わるので、
このグラフより \(y≧0\) となるような範囲が解となるので、答えは$$~~~x≦-3~,~5≦x$$となります。
問題解説(3)
\(x^2\) の係数が負の数であるので、両辺に \(-1\) をかけると、不等号の向きが逆になるので、$$~~~x^2+7×6>0$$となります。
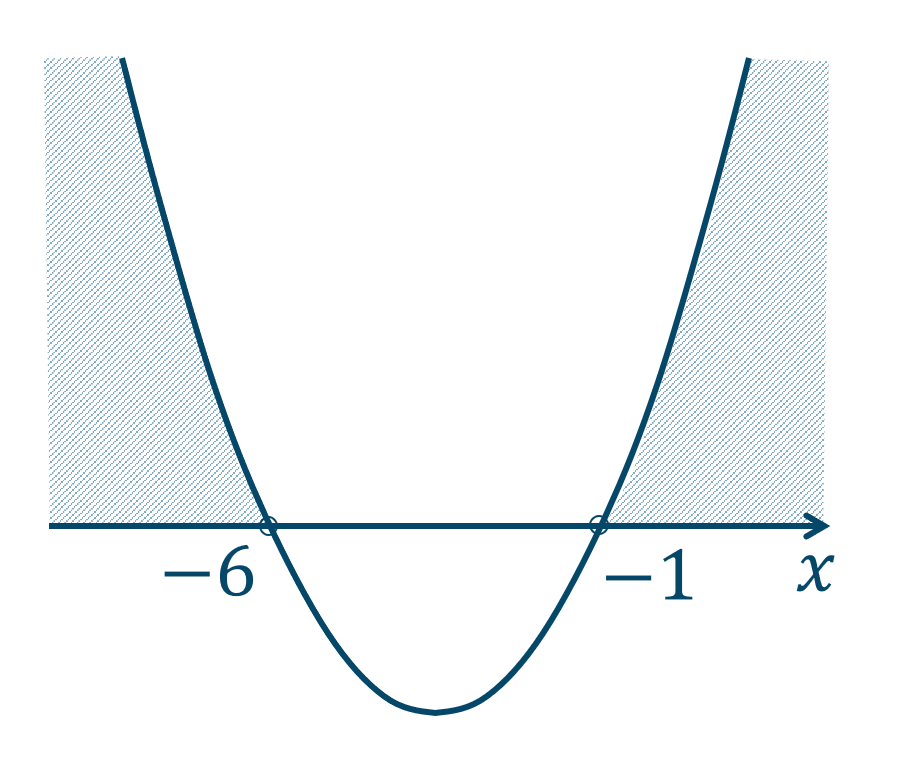
左辺を因数分解すると、$$\hspace{ 10 pt}(x+1)(x+6)>0$$ここで、左辺を \(y\) としたときのグラフは、\(x\) 軸と \(x=-1~,~-6\) で交わるので、
このグラフより \(y>0\) となるような範囲が解となるので、答えは$$~~~x<-6~,~-1<x$$となります。
問題解説(4)
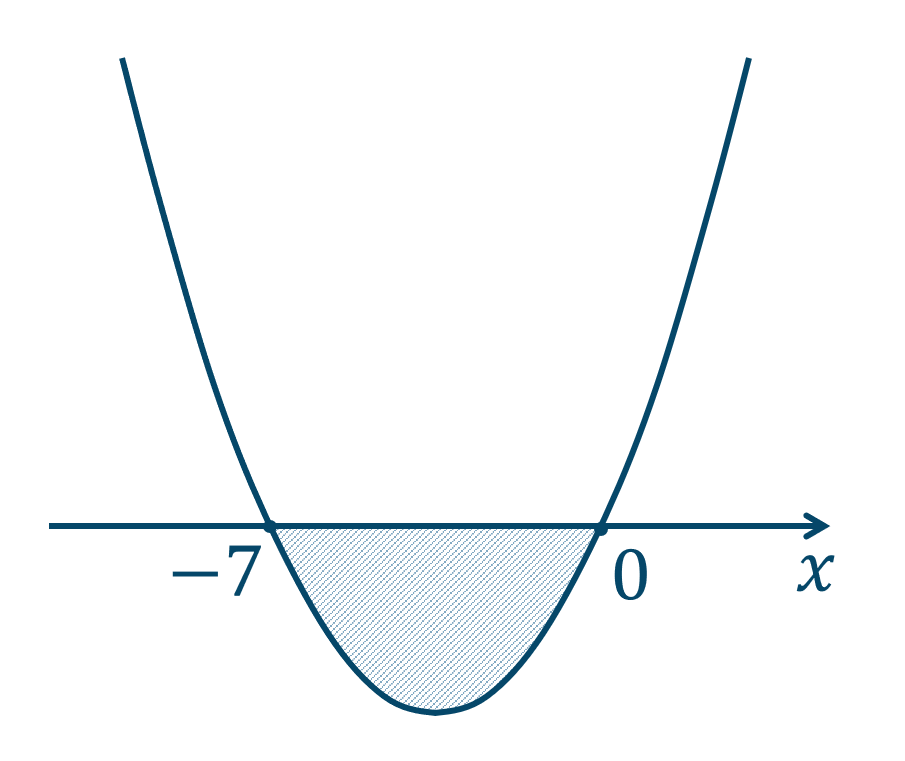
左辺を因数分解すると、$$\hspace{ 10 pt}x(x+7)≦0$$ここで、左辺を \(y\) としたときのグラフは、\(x\) 軸と \(x=-7~,~0\) で交わるので、
このグラフより \(y≦0\) となるような範囲が解となるので、答えは$$~~~-7≦x≦0$$となります。
今回のまとめ
2次不等式の基本的な解法は、グラフを描いてその不等式を満たす範囲を視覚的に捉えることが重要となります。他の解法パターンも押さえておきましょう。