2次不等式の解(解の公式)
② 左辺が因数分解できない場合
左辺=0の2次方程式の解の判別式 \(D\) を考えます。
\(D>0\) となるとき、左辺を \(y\) としたグラフは \(x\) 軸と2点で交わります。
③ その座標を求めるために2次方程式を解の公式を用いて解きます。
④ 求めた2解 \(\alpha~,~\beta\) を用いて因数分解できる場合と同様に2次不等式の解を求めます。
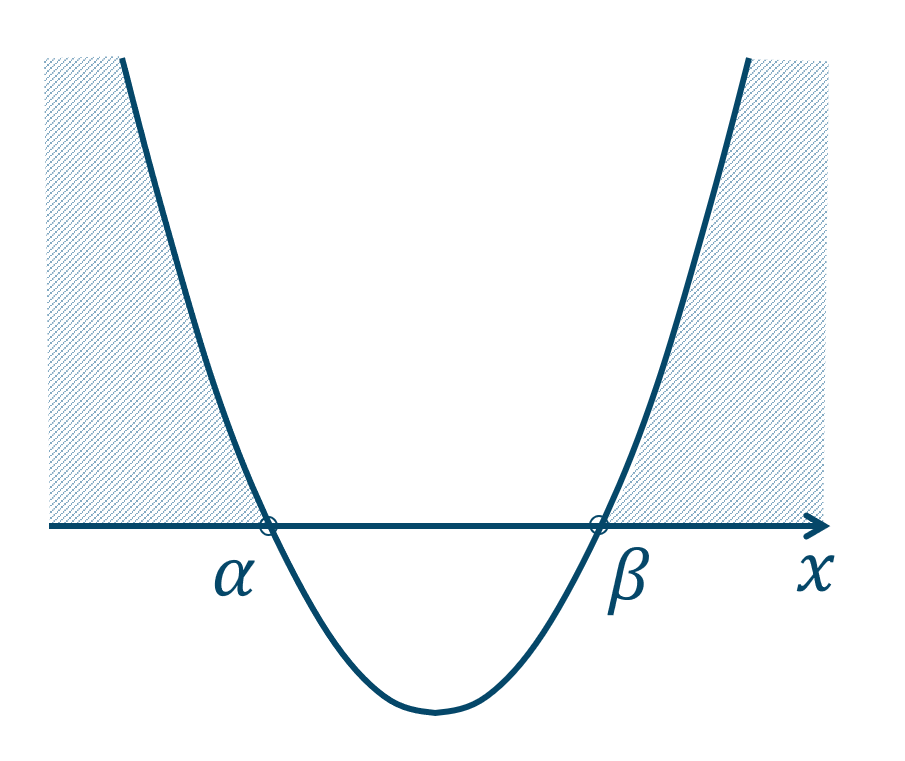
(1) \(ax^2+bx+c≧0\) のとき
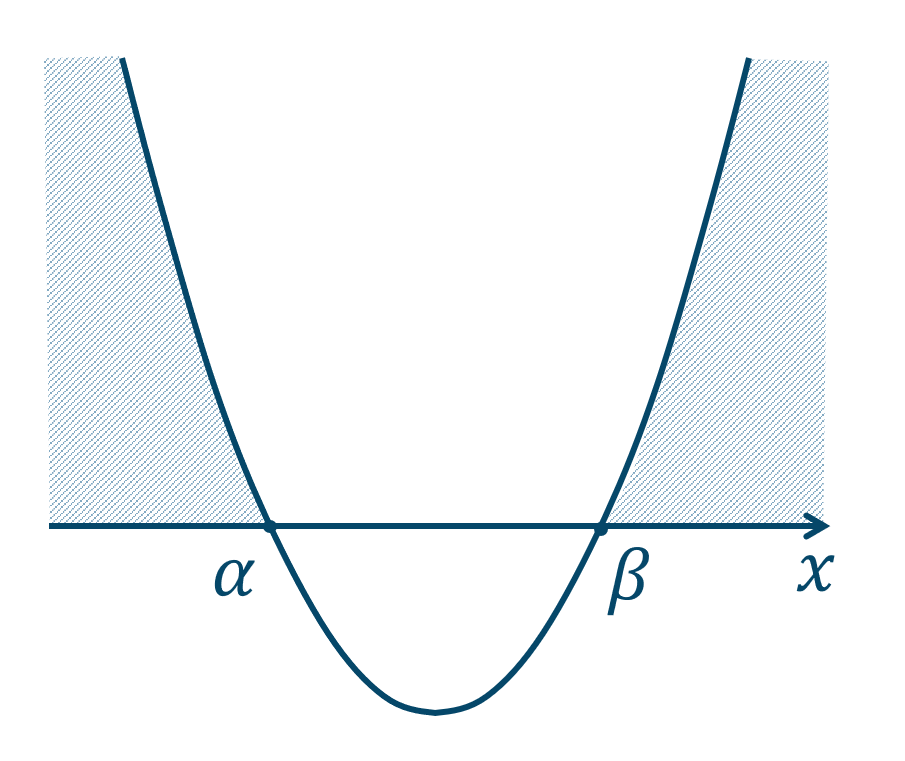
グラフより、答えは
となります。
(2) \(ax^2+bx+c>0\) のとき
グラフより、答えは
となります。
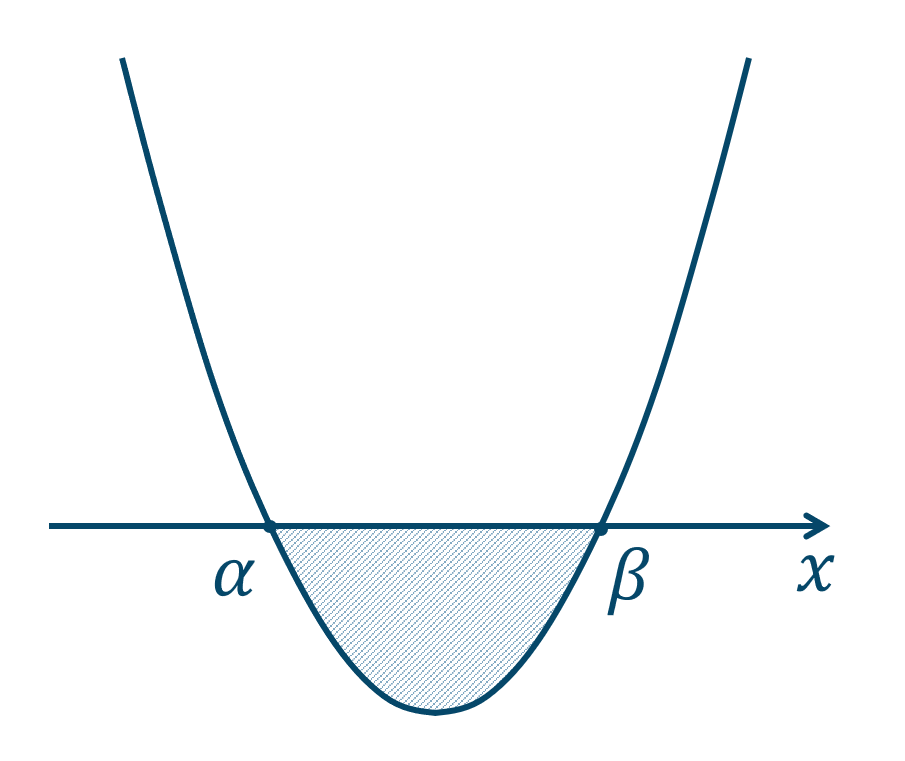
(3) \(ax^2+bx+c≦0\) のとき
グラフより、答えは
となります。
(4) \(ax^2+bx+c<0\) のとき
グラフより、答えは
となります。
問題解説:2次不等式の解③(解の公式)
問題解説(1)
左辺が因数分解できないので、(左辺)=0の2次方程式の判別式 \(D\) を考えると、$$\hspace{ 10 pt}D=2^2-4\cdot1\cdot(-2)$$$$\hspace{ 20 pt}=4+8$$$$\hspace{ 20 pt}=12>0$$よって、\(x\) 軸と2点で交わり、その交点の \(x\) 座標は、$$~~~x^2+2x-2=0$$の解となるので、解の公式より、$$\hspace{ 10 pt}x=\frac{-2\pm\sqrt{2^2-4\cdot1\cdot(-2)}}{2\cdot1}$$$$\hspace{ 18 pt}=\frac{-2\pm\sqrt{4+8}}{2}$$$$\hspace{ 18 pt}=\frac{-2\pm\sqrt{12}}{2}$$$$\hspace{ 18 pt}=\frac{-2\pm2\sqrt{3}}{2}$$分子の各項を \(2\) で割ると、$$\hspace{ 18 pt}=-1\pm\sqrt{3}$$
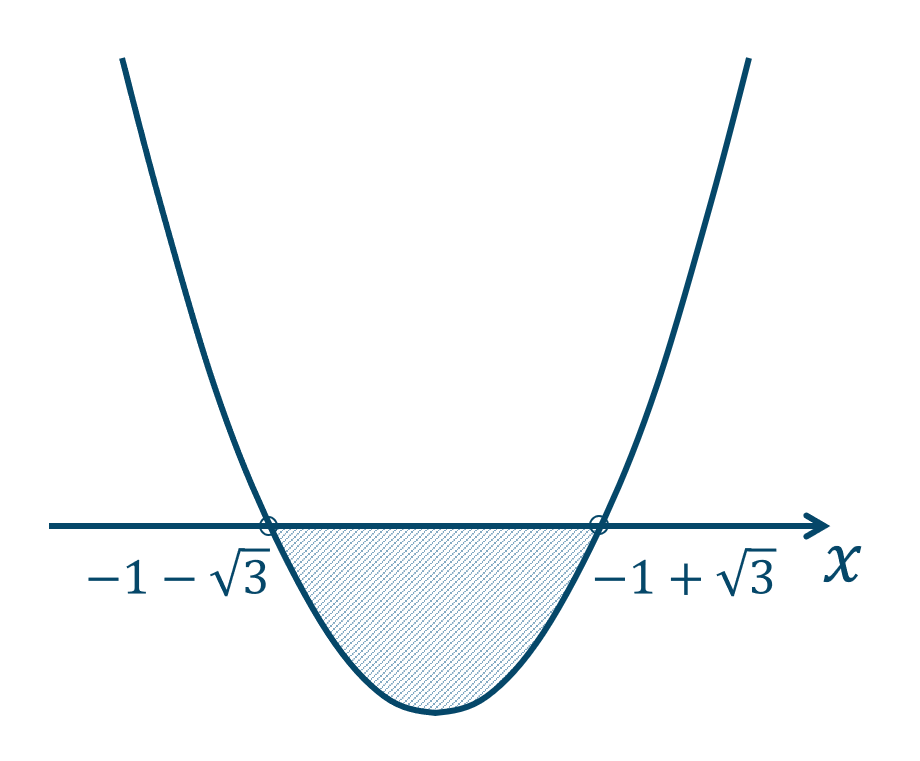
よって、左辺を \(y\) としたときのグラフは、\(x\) 軸と2点$$~~~x=-1-\sqrt{3}~,~-1+\sqrt{3}$$で交わるので、
このグラフより \(y<0\) となるような範囲が解となるので、答えは$$~~~-1-\sqrt{3}<x<-1+\sqrt{3}$$となります。
問題解説(2)
左辺が因数分解できないので、(左辺)=0の2次方程式の判別式 \(D\) を考えると、$$\hspace{ 10 pt}D=(-3)^2-4\cdot2\cdot(-1)$$$$\hspace{ 20 pt}=9+8$$$$\hspace{ 20 pt}=17>0$$よって、\(x\) 軸と2点で交わり、その交点の \(x\) 座標は、$$~~~2x^2-3x-1=0$$の解となるので、解の公式より、$$\hspace{ 10 pt}x=\frac{-(-3)\pm\sqrt{(-3)^2-4\cdot2\cdot(-1)}}{2\cdot2}$$$$\hspace{ 18 pt}=\frac{3\pm\sqrt{9+8}}{4}$$$$\hspace{ 18 pt}=\frac{3\pm\sqrt{17}}{4}$$
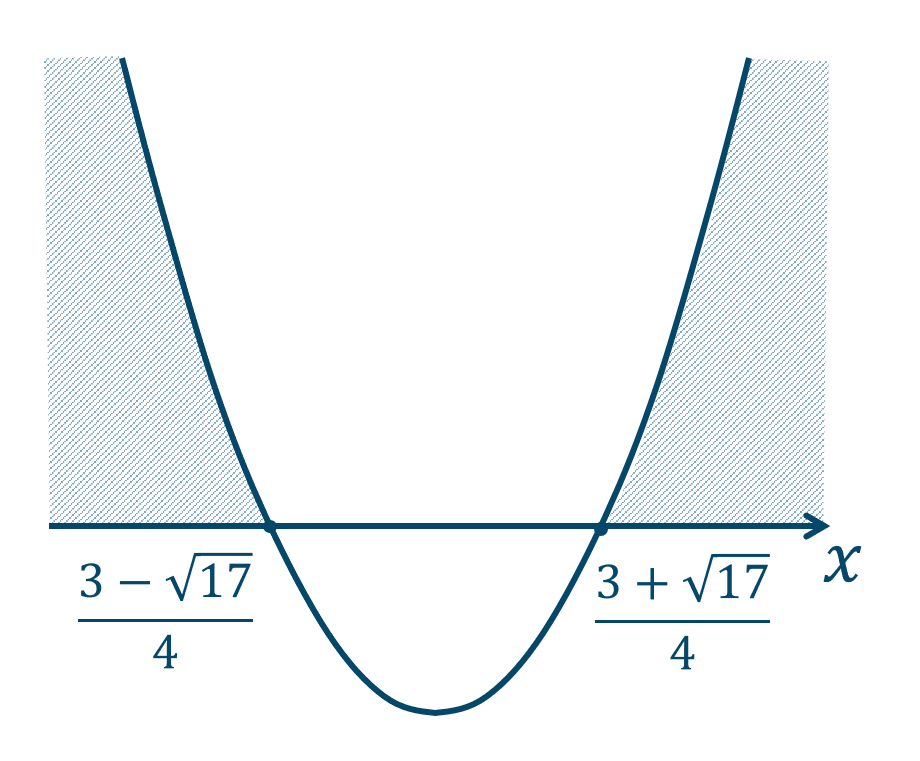
よって、左辺を \(y\) としたときのグラフは、\(x\) 軸と2点$$~~~x=\frac{3-\sqrt{17}}{4}~,~\frac{3+\sqrt{17}}{4}$$で交わるので、
このグラフより \(y≧0\) となるような範囲が解となるので、答えは$$~~~x≦\frac{3-\sqrt{17}}{4}~,~\frac{3+\sqrt{17}}{4}≦x$$となります。
問題解説(3)
\(x^2\) の係数が負の数であるので、両辺に \(-1\) をかけると、不等号の向きが逆になるので、$$~~~x^2-3x+1<0$$となります。
左辺が因数分解できないので、(左辺)=0の2次方程式の判別式 \(D\) を考えると、$$\hspace{ 10 pt}D=(-3)^2-4\cdot1\cdot1$$$$\hspace{ 20 pt}=9-4$$$$\hspace{ 20 pt}=5>0$$よって、\(x\) 軸と2点で交わり、その交点の \(x\) 座標は、$$~~~x^2-3x+1=0$$の解となるので、解の公式より、$$\hspace{ 10 pt}x=\frac{-(-3)\pm\sqrt{(-3)^2-4\cdot1\cdot1}}{2\cdot1}$$$$\hspace{ 18 pt}=\frac{3\pm\sqrt{9-4}}{2}$$$$\hspace{ 18 pt}=\frac{3\pm\sqrt{5}}{2}$$
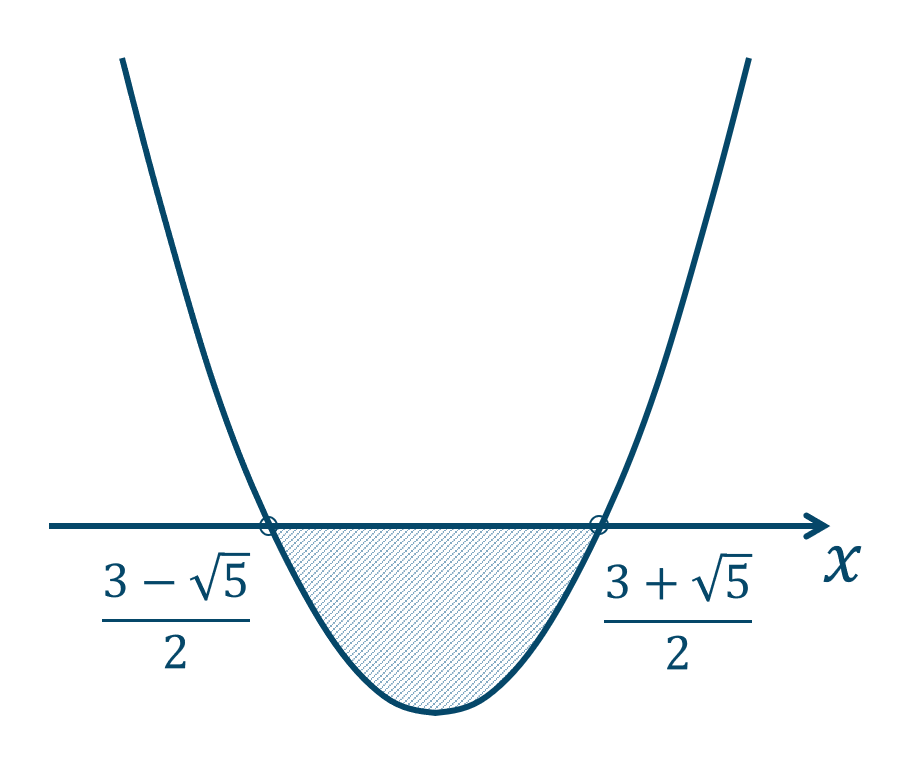
よって、左辺を \(y\) としたときのグラフは、\(x\) 軸と2点$$~~~x=\frac{3-\sqrt{5}}{2}~,~\frac{3+\sqrt{5}}{2}$$で交わるので、
このグラフより \(y<0\) となるような範囲が解となるので、答えは$$~~~\frac{3-\sqrt{5}}{2}< x < \frac{3+\sqrt{5}}{2}$$となります。
今回のまとめ
因数分解できないパターンは判別式より \(x\) 軸との交点の個数を調べましょう。次回は交点がないパターンを解説していきます。