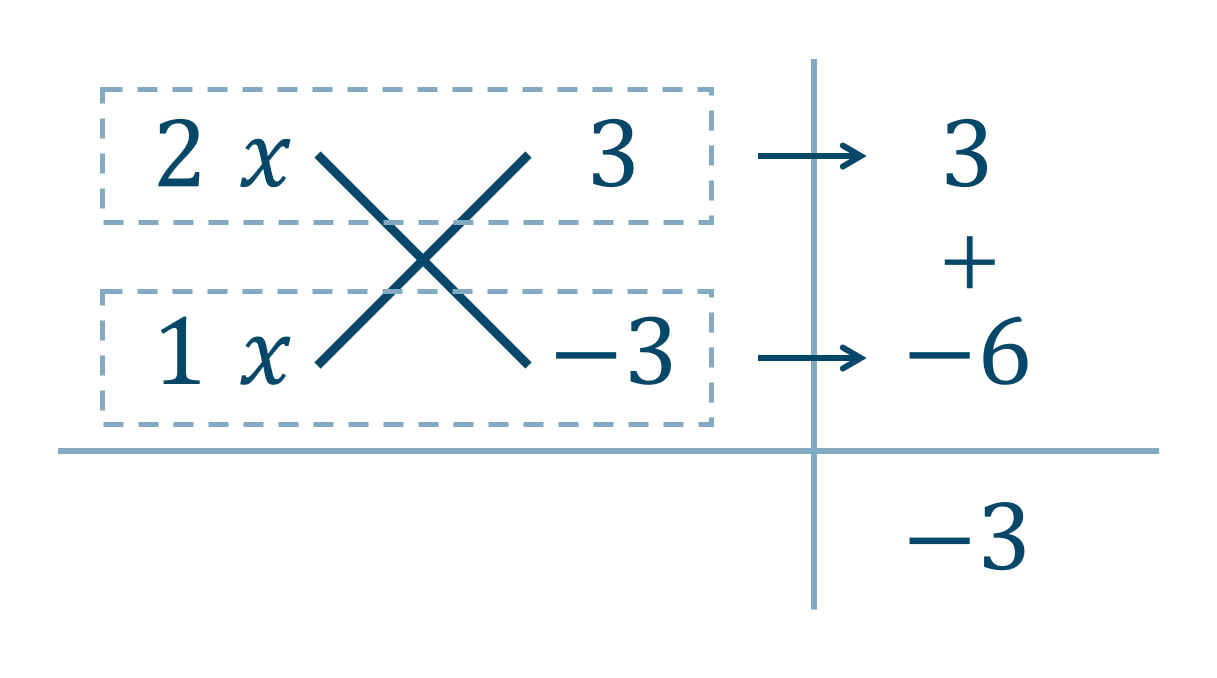連立2次不等式の解の求め方
① それぞれの2次不等式の解を求めます。
② 求めた解を数直線上に表し、共通部分を読み取り解とします。
問題解説:連立2次不等式の解
問題解説(1)
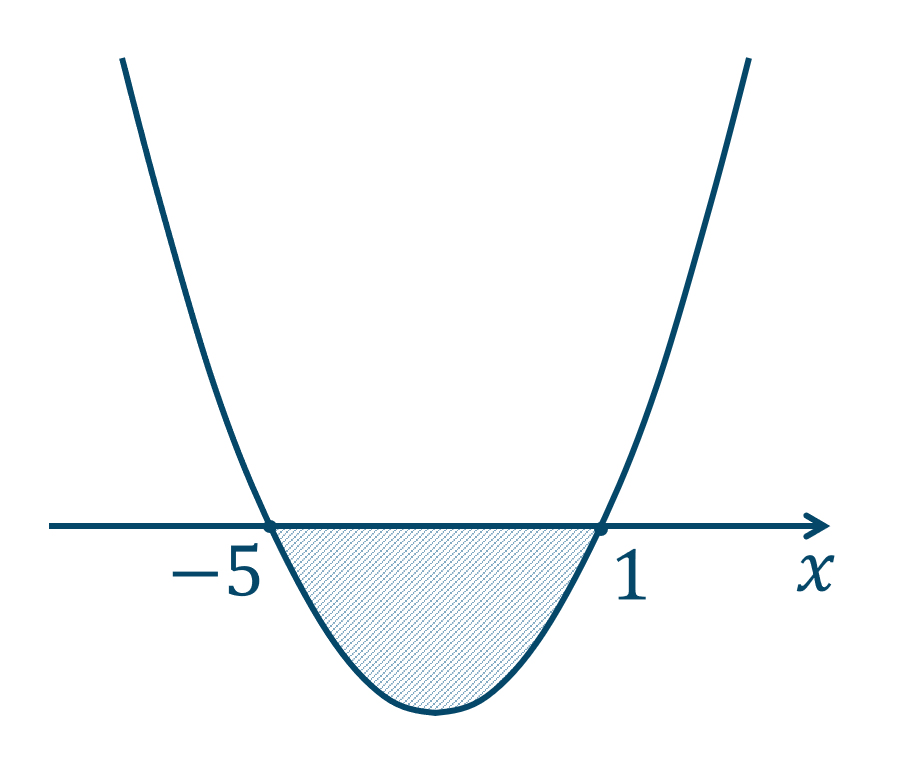
$$\hspace{ 10 pt}\biggl\{ \begin{eqnarray} x^2+4x-5≦0 ~\cdots{\large ①}\\ x^2+3x>0~\cdots{\large ②} \end{eqnarray}$$①より、左辺を因数分解すると、$$\hspace{ 21 pt}x^2+4x-5≦0$$$$\hspace{ 10 pt}(x-1)(x+5)≦0$$ここで、左辺を \(y\) としたグラフを描き \(y≦0\) の範囲を考えると、
よって、$$~~~-5≦x≦1~~\cdots{\large ③}$$
次に、②の左辺を因数分解すると、$$\hspace{ 14 pt}x^2+3x>0$$$$\hspace{ 10 pt}x(x+3)>0$$ここで、左辺を \(y\) としたグラフを描き \(y>0\) の範囲を考えると、
よって、$$~~~x<-3~,~0<x~~\cdots{\large ④}$$
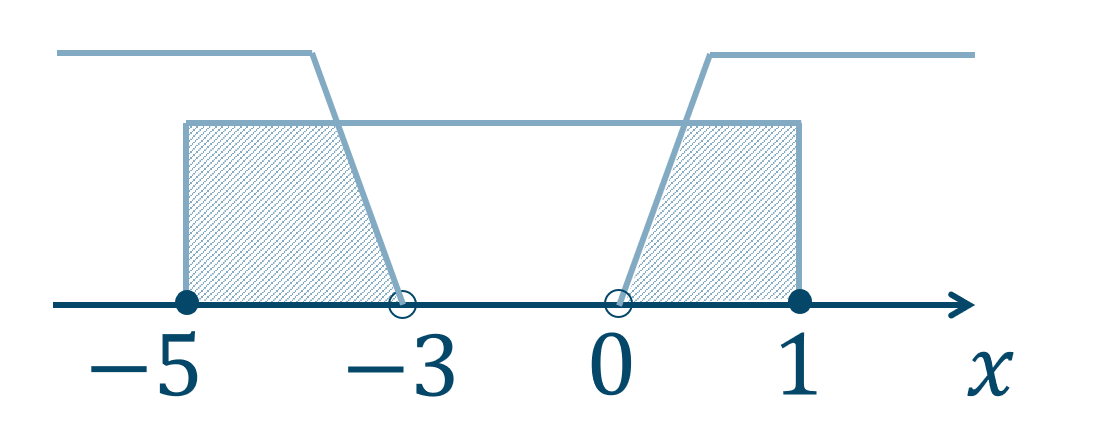
③、④を数直線上に表すと、
よって、答えは$$~~~-5≦x<-3~,~0< x≦1$$となります。
問題解説(2)
$$\hspace{ 10 pt}\biggl\{ \begin{eqnarray} 2x^2-3x-9≦0 ~\cdots{\large ①}\\ x^2-2x+1>0~\cdots{\large ②} \end{eqnarray}$$①より、左辺を因数分解すると、$$\hspace{ 10 pt}2x^2-3x-9≦0$$たすき掛けの表より、
$$\hspace{ 10 pt}(2x+3)(x-3)≦0$$ここで、左辺を \(y\) としたグラフを描き \(y≦0\) の範囲を考えると、
よって、$$~~~-\frac{3}{2}≦x≦3~~\cdots{\large ③}$$
次に、②の左辺を因数分解すると、$$\hspace{ 10 pt}x^2-2x+1>0$$$$\hspace{ 25 pt}(x-1)^2>0$$ここで、左辺を \(y\) としたグラフを描き \(y>0\) の範囲を考えると、
よって、
\(x=1\) 以外のすべての実数\(~~\cdots{\large ④}\)
となります。
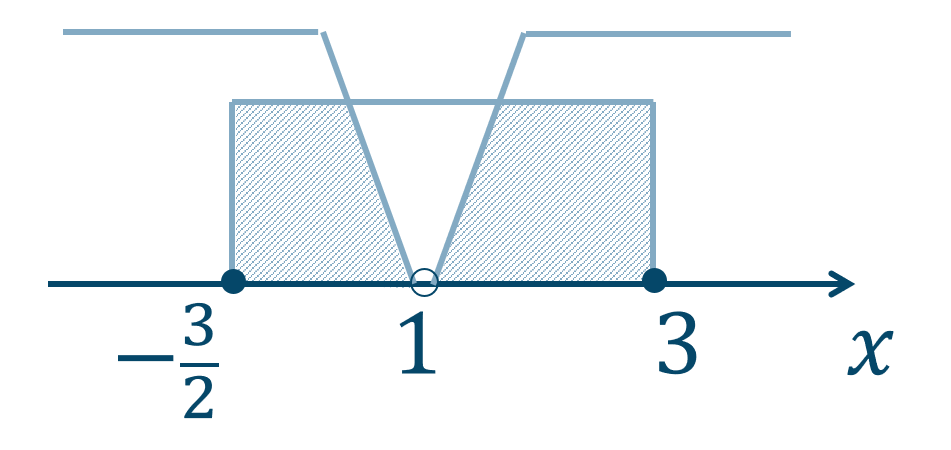
③、④を数直線上に表すと、
よって、答えは$$~~~-\frac{3}{2}≦x<1~,~1< x≦3$$となります。
今回のまとめ
連立2次不等式の解は、それぞれの2次不等式の解を数直線上に表して解を求めることを覚えておきましょう。