余弦定理の解法
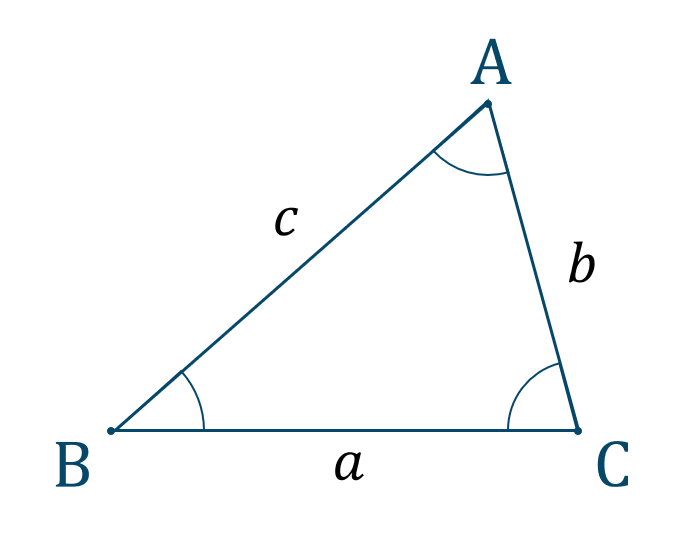
3つの辺と1つの角について、「辺辺辺角」のうちの1つがわかっていないとき、
\(\cos{{\rm A}}\) についての余弦定理
また、他の角でも同様に、
\(\cos{{\rm B}}\) についての余弦定理
\(\cos{{\rm C}}\) についての余弦定理
問題解説:余弦定理
問題解説(1)
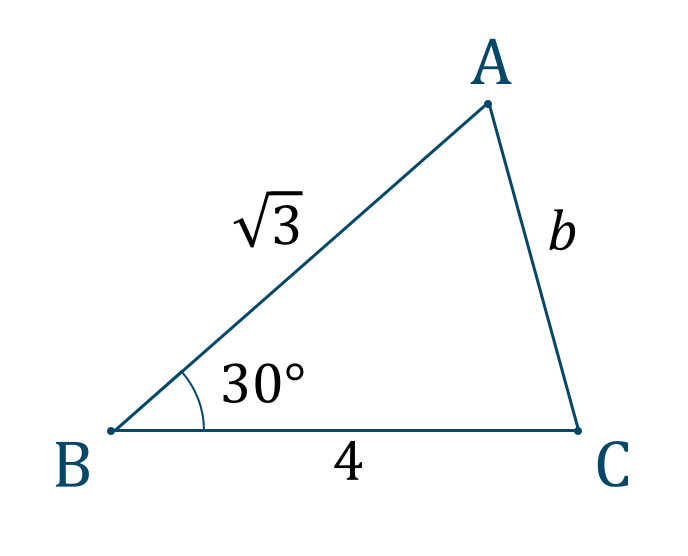
\({\small (1)}\) \(\triangle {\rm ABC}\) について、以下の条件のとき、\(b\) の値を求めよ。$$~~~\angle{\rm B}=30^\circ~,~a=4~,~c=\sqrt{3}$$
与えられた図形は次のようになります。
\(\cos{{\rm B}}\) について余弦定理を用いると、$$\hspace{ 10 pt}b^2=4^2+(\sqrt{3})^2-2\cdot4\cdot\sqrt{3}\cdot\cos{30^\circ}$$$$\hspace{ 21 pt}=16+3-8\sqrt{3}\frac{\sqrt{3}}{2}$$$$\hspace{ 21 pt}=19-4\cdot3$$$$\hspace{ 21 pt}=19-12$$$$\hspace{ 21 pt}=7$$ここで、\(b>0\) より、$$\hspace{ 10 pt}b=\sqrt{7}$$
よって、答えは$$~~~b=\sqrt{7}$$となります。
問題解説(2)
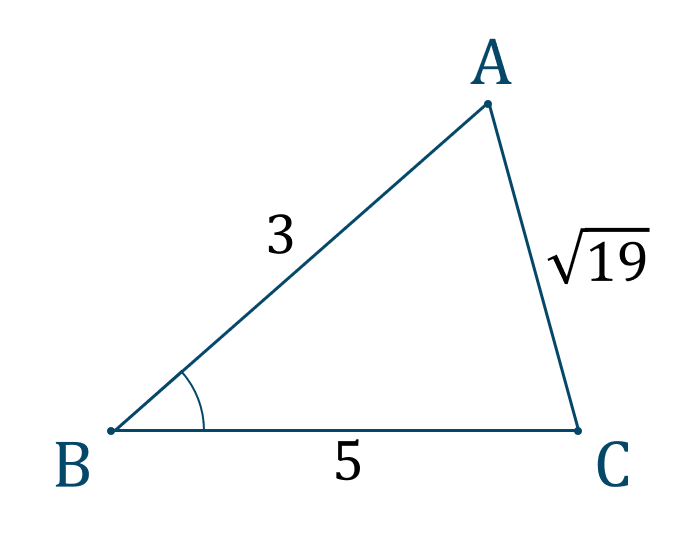
\({\small (2)}\) \(\triangle {\rm ABC}\) について、以下の条件のとき、\(\angle{\rm B}\) の値を求めよ。$$~~~a=5~,~b=\sqrt{19}~,~c=3$$
与えられた図形は次のようになります。
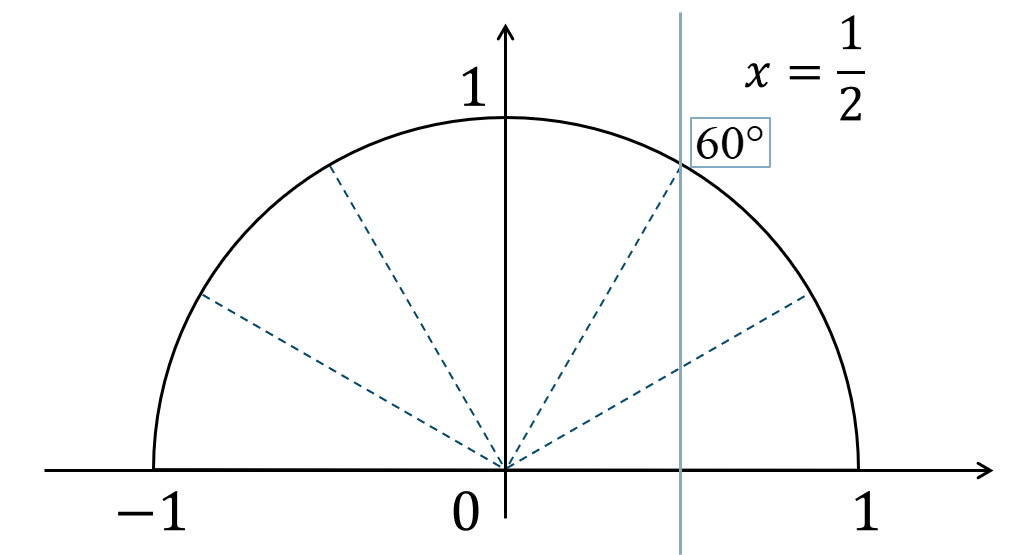
\(\cos{{\rm B}}\) について余弦定理を用いると、$$\hspace{ 10 pt}(\sqrt{19})^2=5^2+3^2-2\cdot5\cdot3\cdot\cos{{\rm B}}$$$$\hspace{ 31 pt}19=25+9-30\cos{{\rm B}}$$$$\hspace{ 31 pt}19=34-30\cos{{\rm B}}$$\(19\) を右辺に、\(-30\cos{{\rm B}}\) を左辺に移項すると、$$\hspace{ 10 pt}30\cos{{\rm B}}=34-19$$$$\hspace{ 10 pt}30\cos{{\rm B}}=15$$両辺を\(30\) で割ると、$$\hspace{ 10 pt}\cos{{\rm B}}=\frac{1}{2}$$単位円上に表すと次のようになります。
よって、答えは$$~~~\angle{\rm B}=60^\circ$$となります。
今回のまとめ
余弦定理の用いる問題は、「辺辺辺角」が条件で与えられてどれか1つがわかっていないパターンとなります。使い方も合わせてしっかりと覚えておきましょう。