二項定理の解法
例えば、\((a+b)^3\) の展開式を考えてみましょう。$$~~~(a+b)^3=(a+b)(a+b)(a+b)$$と式変形できるので、
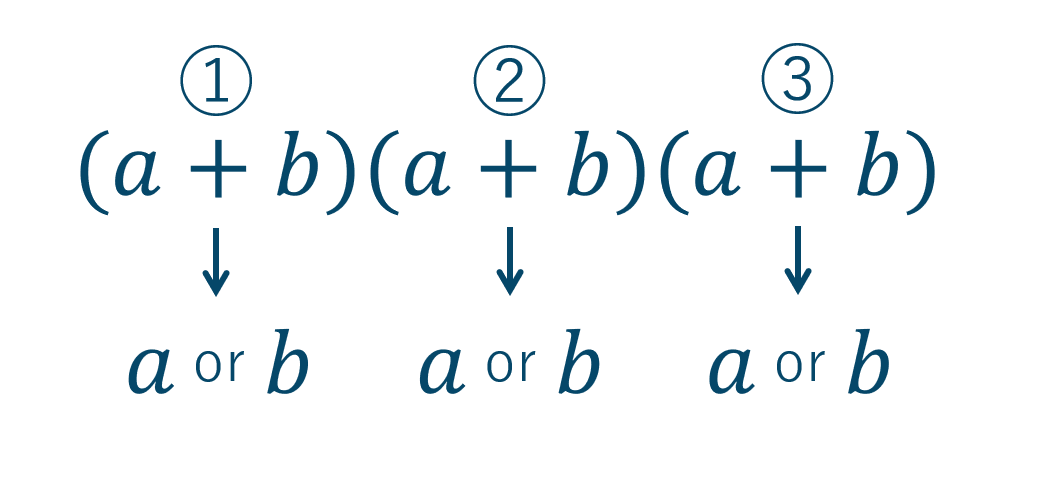
それぞれを①〜③の部屋と考えて、各部屋から \(a\) または \(b\) を取り出してかけ算していくと展開したときの項がでてきます。
例えば、
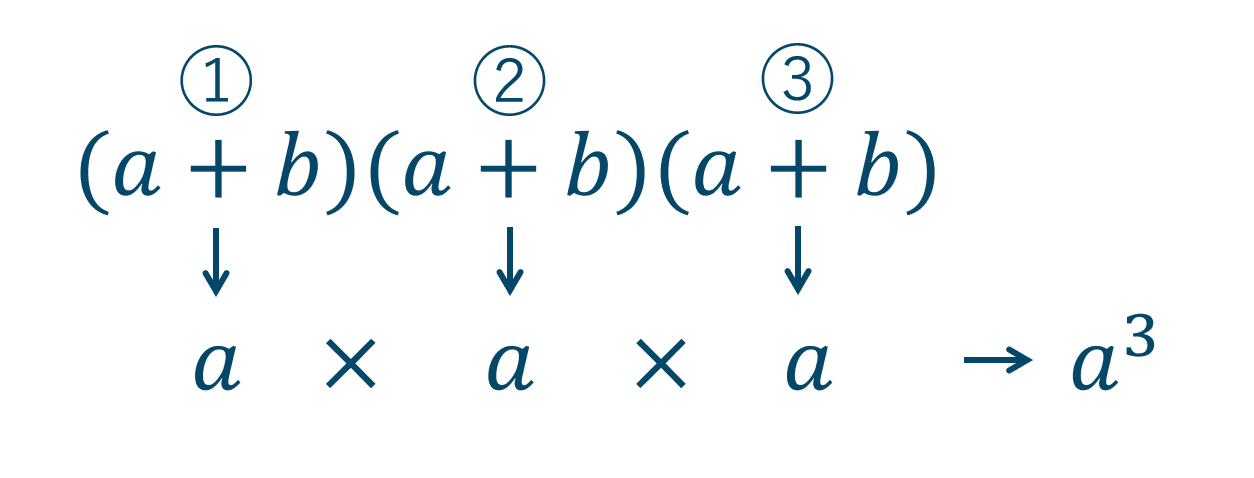
このときは、\(a^3\) の項がでてきます。
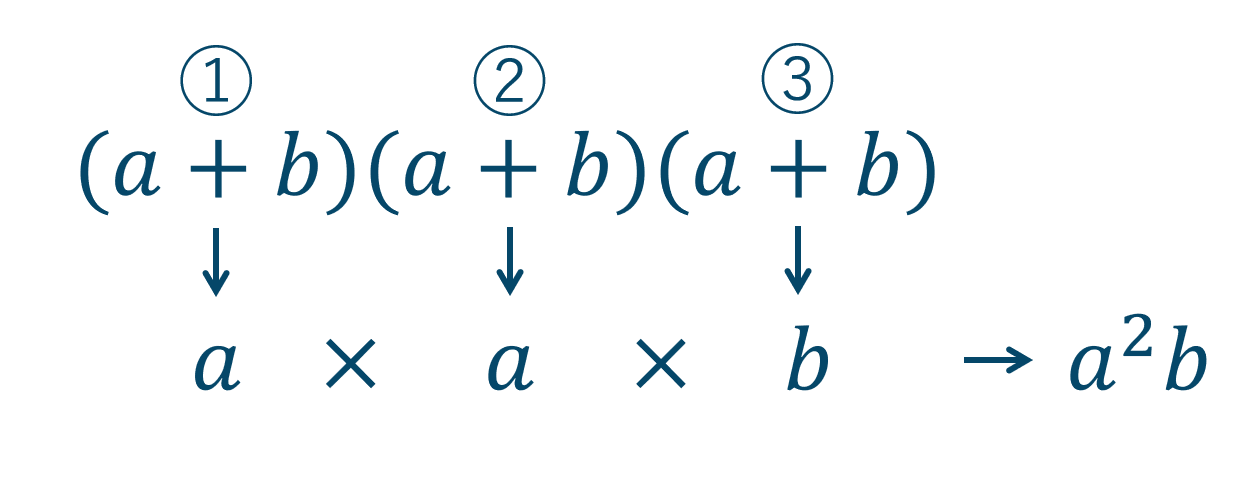
このときは、\(a^2b\) の項がでてきます。
ここで、\(a^2b\) の項の取り出し方を考えてみましょう。
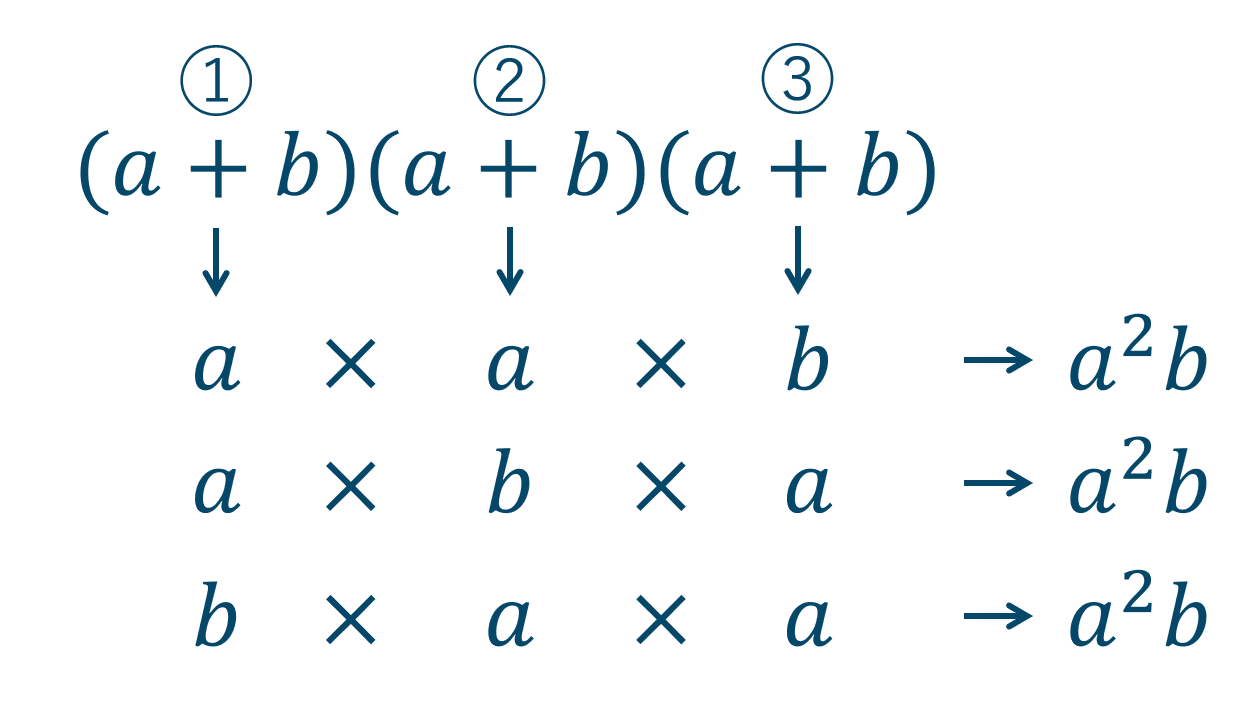
上の図のように \(a^2b\) の取り出し方は \(3\) 通りあるので、\(a^2b\) の係数が \(3\) となります。
この係数の計算は、3か所から \(b\) を取り出す部屋1か所を選ぶ組合せで計算できるので \({}_{3}{\rm C}_{1}\) で計算できます。このとき、選ばれなかった2か所には \(a\) が自動で入るので、\(a\) の部屋の選び方は考えなくて良くなります。
以上よりまとめると、
\((a+b)^n\) を展開したときの項 \(a^pb^q\)
(ただし、 \(p+q=n\) ) は、
よって、
と計算できます。
・二項定理と展開式
\((a+b)^n\) の展開式は次のようになります。
$$~~~~~~(a+b)^n$$$$~={}_{n}{\rm C}_{0}a^n+{}_{n}{\rm C}_{1}a^{n-1}b+{}_{n}{\rm C}_{2}a^{n-2}b^2$$$$~~~~~~~~~~\cdots +{}_{n}{\rm C}_{r}a^{n-r}b^{r}$$$$\hspace{50pt}+\cdots+{}_{n}{\rm C}_{n-1}ab^{n-1}+{}_{n}{\rm C}_{n}b^n$$
問題解説:二項定理
問題解説(1)
\({\small (1)}~\)\((a-2b)^5\) を展開せよ。
二項定理より、$$~~~~~~(a-2b)^5$$$$~={}_{5}{\rm C}_{0}a^5+{}_{5}{\rm C}_{1}a^4(-2b)+{}_{5}{\rm C}_{2}a^3(-2b)^2$$$$~~~~~+{}_{5}{\rm C}_{3}a^2(-2b)^3+{}_{5}{\rm C}_{4}a(-2b)^4+{}_{5}{\rm C}_{5}(-2b)^5$$$$~=a^5+5\cdot(-2)a^4b+10\cdot 4a^3b^2$$$$~~~~~+10\cdot(-8)a^2b^3+5\cdot16ab^4+1\cdot(-32)b^5$$$$~=a^5-10a^4b+40a^3b^2$$$$~~~~~~~~~-80a^2b^3+80ab^4-32b^5$$
よって、答えは$$a^5-10a^4b+40a^3b^2-80a^2b^3+80ab^4-32b^5$$となります。
問題解説(2)
\({\small (2)}~\)\((3x-2y)^5\) を展開したときの \(x^2y^3\) の係数を求めよ。
\((3x-2y)^5\) を展開したときの項は、\({}_{5}{\rm C}_{q}\cdot (3x)^p \cdot (-2y)^q \) と表されて \(p+q=5\) となります。
ここで、\(x^2y^3\) の項は、\(p=2~,~q=3\) のときであるので、\(3x\) を2つ、\(-2y\) を3つ取り出せばよいので、
これを式にすると、$$~~~~~~{}_{5}{\rm C}_{3}\cdot (3x)^2 \cdot (-2y)^3$$$$~=\frac{5\cdot4\cdot3}{3\cdot2\cdot1}\cdot(3x)^2\cdot(-2y)^3$$$$~=10\cdot9\cdot(-8)x^2y^3$$$$~=-720x^2y^3$$
よって、\(x^2y^3\) の係数は \(-720\) となります。
問題解説(3)
\({\small (3)}~\)\((x^2-3y)^6\) を展開したときの \(x^8y^2\) の係数を求めよ。
\((x^2-3y)^6\) を展開したときの項は、\({}_{6}{\rm C}_{q}\cdot (x^2)^p \cdot (-3y)^q \) と表されて \(p+q=6\) となります。
ここで、\(x^8y^2\) の項は、\(2p=8~,~q=2\) すなわち \(p=4~,~q=2\) のときであるので、\(x^2\) を4つ、\(-3y\) を2つ取り出せばよいので、
これを式にすると、$$~~~~~~{}_{6}{\rm C}_{2}\cdot (x^2)^4 \cdot (-3y)^2$$$$~=\frac{6\cdot5}{2\cdot1}\cdot(x^2)^4\cdot(-3y)^2$$$$~=15\cdot9x^8y^2$$$$~=135x^8y^2$$
よって、\(x^8y^2\) の係数は \(135\) となります。
今回のまとめ
二項定理を用いると展開した式の項の係数を求めることができます。計算するとき、取り出し方の組合せをかけるのを忘れないようにしましょう。



