解と係数の関係を用いた２次方程式の解の符号の解法
(ⅰ) ２つの解がともに正の解のとき、
このとき以下の３つの条件が成り立てばよい、
(ⅱ) ２つの解がともに負の解のとき、
このとき以下の３つの条件が成り立てばよい、
(ⅲ) 異符号の解（１つが正の解でもう１つが負の解）であるとき、
次の１つの条件が成り立てばよい、
問題解説：２次方程式の解の符号
問題解説(1)
\({\small (1)}~\) ２つの解がともに負
２次方程式 \(x^2-kx+k+8=0\) の２つの解を \(\alpha~,~\beta\) とするとき、解と係数の関係より、$$~~~\Biggl\{ \begin{eqnarray} ~\alpha+\beta=-\frac{-k}{1}=k~\cdots{\large ①}\\ ~~\alpha\beta=\frac{k+8}{1}=k+8~\cdots{\large ②}\end{eqnarray}$$また、この２次方程式の解の判別式を \(D\) とすると、$$~~~D=(-k)^2-4\cdot1\cdot(k+8)$$$$\hspace{ 18 pt}=k^2-4k-32$$$$\hspace{ 18 pt}=(k+4)(k-8)~\cdots{\large ③}$$
２つの解がともに負となるには、$$~~~\Biggl\{ \begin{eqnarray}~\alpha+\beta<0 \\ ~\alpha\beta>0 \\ ~D>0 \end{eqnarray}$$であればよい。
\(\alpha+\beta<0\) と①より、$$~~~k<0~\cdots{\large ❶}$$
\(\alpha\beta>0\) と②より、$$~~~k+8>0$$$$\hspace{ 25 pt}k>-8~\cdots{\large ❷}$$
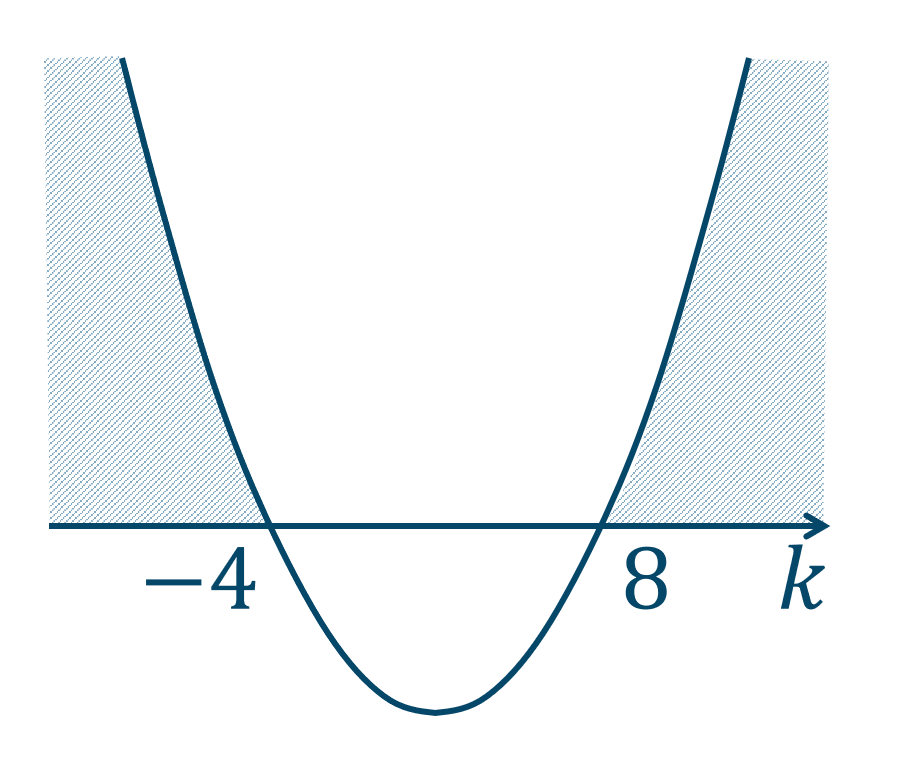
\(D>0\) と③より、$$~~~(k+4)(k-8)>0$$次のグラフより、
$$~~~k<-4~,~8<k~\cdots{\large ❸}$$
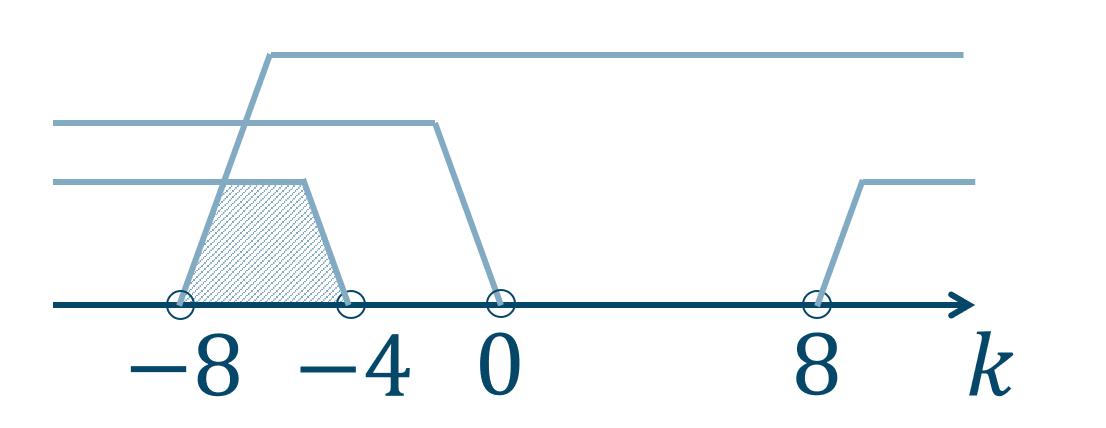
以上より、❶と❷と❸を数直線上に表すと次のようになります。
よって、答えは \(-8<k<-4\) となります。
問題解説(2)
\({\small (2)}~\) 異符号の解
２つの解が異符号となるのは、$$~~~\alpha\beta<0$$であればよい。
問題(1)の②の式 \(\alpha\beta=k+8\) より、$$~~~k+8<0$$$$\hspace{ 25 pt}k<-8$$よって、答えは \(k<-8\) となります。
今回のまとめ
２次方程式の解の符号の条件は、解と係数の関係を用いた条件式を解きましょう。また、判別式も用いることも忘れないようにしましょう。
