直線上の線分の長さ・内分点・外分点の求め方
2点 \(A(a)~,~B(b)\) の間の距離 \(AB\) は次のようになります。
線分の長さは、「差の絶対値」と覚えましょう。
・内分点
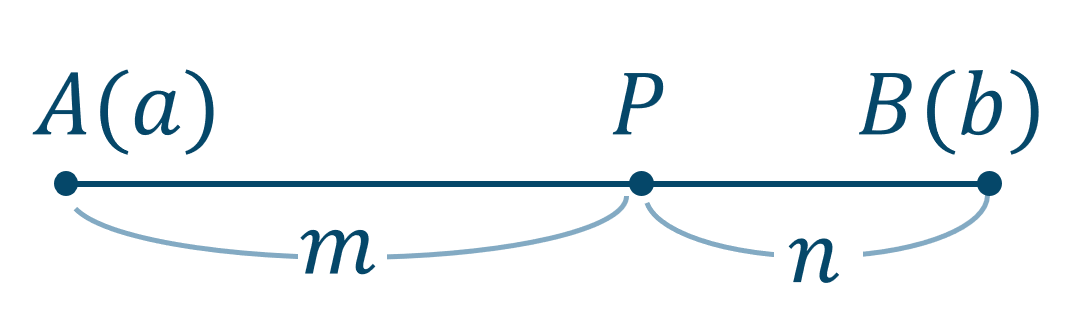
2点 \(A(a)~,~B(b)\) を \(m:n\) に内分する点は次のようになります。
また、数直線上の位置は、次のようになります。
分子が「比と座標のたすき掛けの和」
分母が「比の値の和」
と覚えましょう。
また、中点の座標は次のようになります。
「座標の和÷2」と覚えましょう。
・外分点
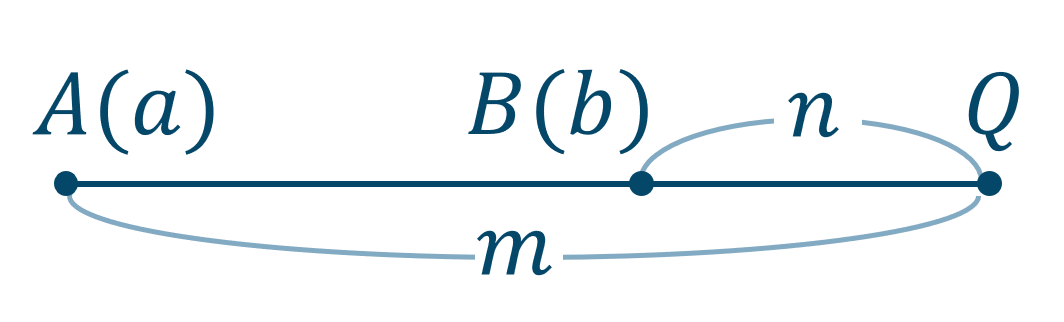
2点 \(A(a)~,~B(b)\) を \(m:n\) に外分する点は次のようになります。
計算するだけなら内分点の公式を、\(m:-n\) として計算しましょう。
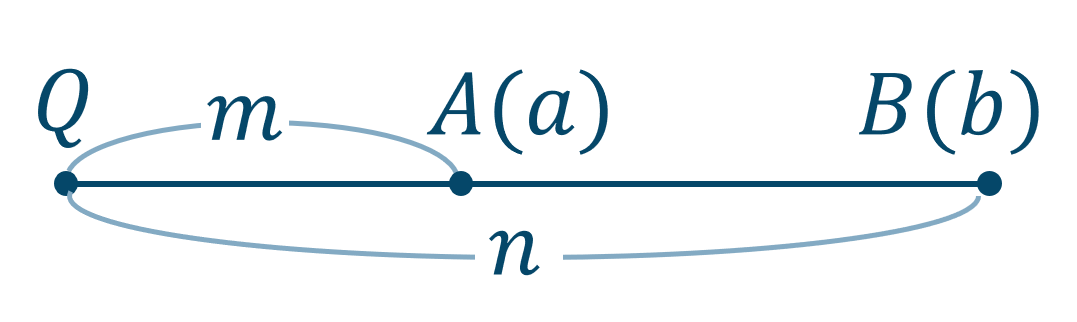
また、数直線上の位置は、
\(m>n\) のとき、
\(m<n\) のとき、
問題解説:直線上の線分の長さ・内分点・外分点
問題解説(1)
\({\small (1)}~\)線分 \(AB\) の長さ
2点 \(A(-3)~,~B(1)\) より、
$$~~~AB=|1-(-3)|$$$$\hspace{ 25 pt}=|1+3|$$$$\hspace{ 25 pt}=|4|$$$$\hspace{ 25 pt}=4$$よって、答えは \(4\) となります。
問題解説(2)
\({\small (2)}~\)線分 \(BC\) の長さ
2点 \(B(1)~,~C(5)\) より、$$~~~BC=|5-1|$$$$\hspace{ 25 pt}=|4|$$$$\hspace{ 25 pt}=4$$よって、答えは \(4\) となります。
問題解説(3)
\({\small (3)}~\)線分 \(AB\) の中点の座標 \(M\)
2点 \(A(-3)~,~B(1)\) において、中点となるので、$$~~~~~~\frac{-3+1}{2}$$$$~=\frac{-2}{2}$$$$~=-1$$よって、答えは \(M(-1)\) となります。
問題解説(4)
\({\small (4)}~\)線分 \(AC\) を \(2:1\) に内分する点の座標 \(P\)
2点 \(A(-3)~,~C(5)\) において、線分 \(AC\) を \(2:1\) に内分するので、$$~~~~~~\frac{1\cdot(-3)+2\cdot5}{2+1}$$$$~=\frac{-3+10}{3}$$$$~=\frac{7}{3}$$よって、答えは \(P\left( {\Large \frac{7}{3}} \right) \) となります。
問題解説(5)
\({\small (5)}~\)線分 \(BC\) を \(3:1\) に外分する点の座標 \(Q\)
2点 \(B(1)~,~C(5)\) において、線分 \(BC\) を\(3:1\) に外分するので、$$~~~~~~\frac{-1\cdot1+3\cdot5}{3-1}$$$$~=\frac{-1+15}{2}$$$$~=\frac{14}{2}$$$$~=7$$よって、答えは \(Q(7)\) となります。
今回のまとめ
内分点と外分点の座標を求めるときは、線分の表記の順番と比の順番に注意して計算しましょう。