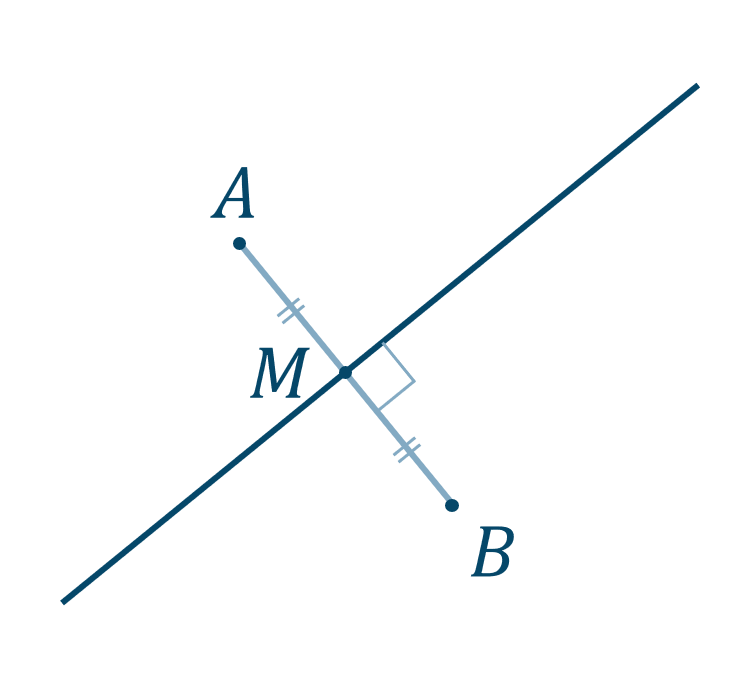
垂直二等分線の方程式

2018.05.052020.06.09

垂直二等分線の方程式の解法
問題解説：垂直二等分線の方程式
今回のまとめ

垂直二等分線の方程式の解法

Point：垂直二等分線の方程式線分 $AB$ に対する垂直二等分線の方程式を求める解法の手順は、
① 垂直二等分線の傾きを $m_1$ とし線分 $AB$ の傾きを $m_2$ とするとき、

$$m_1 \times m_2=-1$$

これより、$m_1$ を求めます。
② 線分 $AB$ の中点 $M$ の座標 $(p,q)$ を求めます。
② これらより、垂直二等分線の方程式は、傾き $m_1$ で点 $(p,q)$ を通るので、

$$y-q=m_1(x-p)$$

となります。

問題解説：垂直二等分線の方程式

問題２点 $A(2,3)~,~B(-2,1)$ を結ぶ線分 $AB$ の垂直二等分線の方程式を求めよ。

２点 $A(2,3)~,~B(-2,1)$ について、直線 $AB$ の傾きは、$$~~~~~~\frac{1-3}{-2-2}$$$$~=\frac{-2}{-4}$$$$~=\frac{1}{2}$$また、垂直二等分線の傾きを $m$ とすると、垂直に交わる条件より、$$~~~\frac{1}{2}\times m=-1$$両辺に $2$ をかけると、$$\hspace{ 10 pt} m=-2$$
次に、線分 $AB$ の中点は、$$~~~~~~\left( \frac{2-2}{0}~,~\frac{3+1}{2} \right)$$$$~=\left(0~,~\frac{4}{2}\right)$$$$~=(0,2)$$
よって、垂直二等分線の方程式は、傾きが $-2$ で点 $(0,2)$ を通るので、$$\hspace{10pt}y-2=-2(x-0)$$$$\hspace{ 10 pt}y-2=-2x$$移項すると、$$\hspace{ 10 pt}y=-2x+2$$よって、答えは $y=-2x+2$ となります。