点と直線との距離

2018.05.062020.06.09

点と直線との距離の公式と解法
問題解説：点と直線との距離
今回のまとめ

点と直線との距離の公式と解法

Point：点と直線との距離の公式点 $P(p,q)$ と直線 $l:~ax+by+c=0$ との距離 $d$ は、次の図のように垂直に交わる最短距離となり、その値は次の式で表されます。

$$d=\frac{|ap+bq+c|}{\sqrt{a^2+b^2}}$$

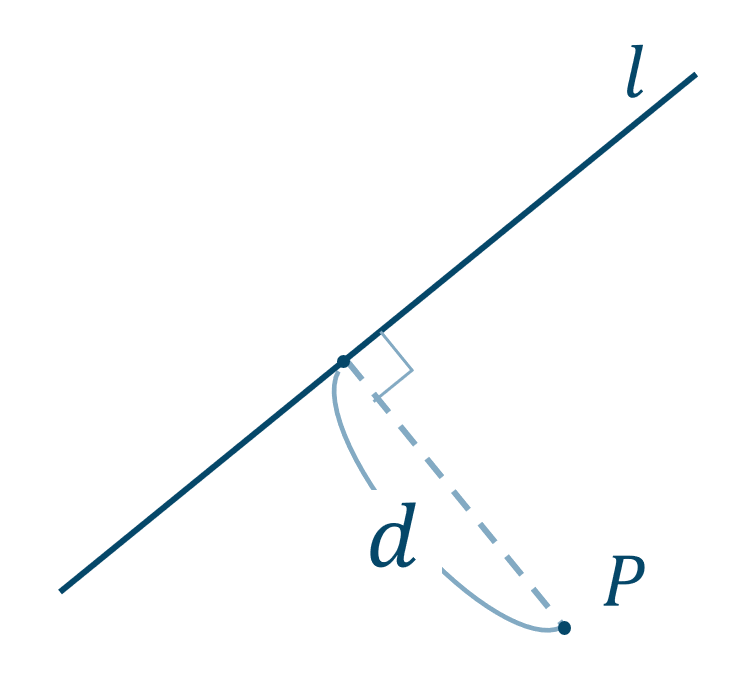
分子は「直線の左辺に点を代入した絶対値」
分母は「係数の２乗の和のルート」
と覚えましょう。

問題解説：点と直線との距離

問題解説(1)

問題次の点と直線との距離を求めよ。$${\small (1)}~x-2y+4=0~,~(0,0)$$

点 $(0,0)$ と直線 $x-2y+4=0$ との距離 $d$ は公式より、$$~~~d=\frac{|0-2\cdot 0+4|}{\sqrt{1^2+(-2)^2}}$$$$\hspace{ 16 pt}=\frac{|4|}{\sqrt{1+4}}$$$$\hspace{ 16 pt}=\frac{4}{\sqrt{5}}$$分母分子に $\sqrt{5}$ をかけると、$$\hspace{ 16 pt}=\frac{4}{\sqrt{5}}\times\frac{\sqrt{5}}{\sqrt{5}}$$$$\hspace{ 16 pt}=\frac{4\sqrt{5}}{5}$$よって、答えは ${\Large \frac{4\sqrt{5}}{5}}$ となります。

問題解説(2)

問題次の点と直線との距離を求めよ。$${\small (2)}~x-2y+4=0~,~(1,5)$$

点 $(1,5)$ と直線 $x-2y+4=0$ との距離 $d$ は公式より、$$~~~d=\frac{|1-2\cdot 5+4|}{\sqrt{1^2+(-2)^2}}$$$$\hspace{ 16 pt}=\frac{|1-10+4|}{\sqrt{1+4}}$$$$\hspace{ 16 pt}=\frac{|-5|}{\sqrt{5}}$$$$\hspace{ 16 pt}=\frac{5}{\sqrt{5}}$$分母分子に $\sqrt{5}$ をかけると、$$\hspace{ 16 pt}=\frac{5}{\sqrt{5}}\times\frac{\sqrt{5}}{\sqrt{5}}$$$$\hspace{ 16 pt}=\frac{5\sqrt{5}}{5}$$$$\hspace{ 16 pt}=\sqrt{5}$$よって、答えは $\sqrt{5}$ となります。

問題解説(3)

問題次の点と直線との距離を求めよ。$${\small (3)}~y=-\frac{3}{4}x+1~,~(2,3)$$

直線 $y=-\frac{3}{4}x+1$ について、$$~~~y=-\frac{3}{4}x+1$$移項すると、$$\hspace{ 10 pt}\frac{3}{4}x+y-1=0$$両辺に $4$ をかけると、$$\hspace{ 10 pt}3x+4y-4=0$$よって、点 $(2,3)$ と直線 $3x+4y-4=0$ との距離 $d$ は公式より、$$~~~d=\frac{|3\cdot2+4\cdot3-4|}{\sqrt{3^2+4^2}}$$$$\hspace{ 16 pt}=\frac{|6+12-4|}{\sqrt{9+16}}$$$$\hspace{ 16 pt}=\frac{|14|}{\sqrt{25}}$$$$\hspace{ 16 pt}=\frac{14}{5}$$よって、答えは ${\Large \frac{14}{5}}$ となります。