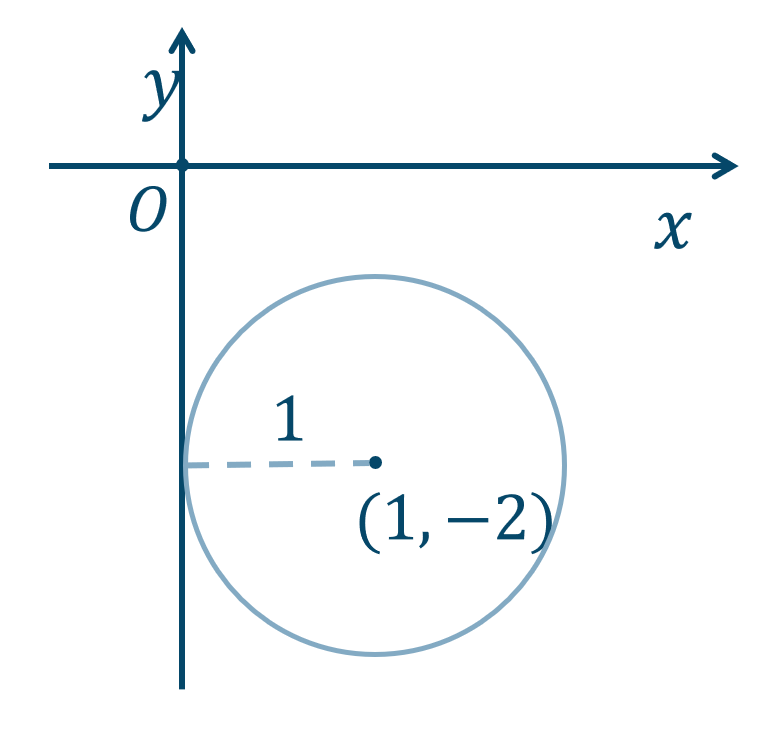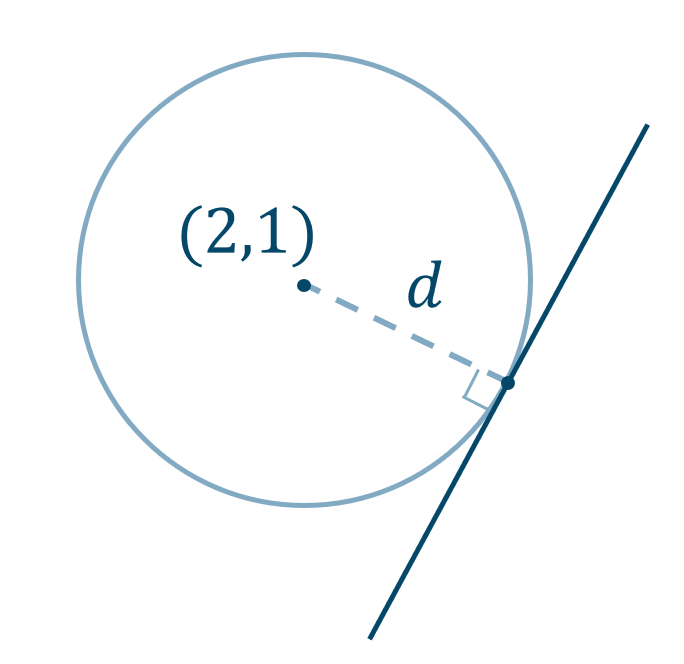接する条件が与えられた円の方程式の決定
中心が \((a,b)\) ので \(x\) 軸と接するとき、中心の \(y\) 座標より半径は、$$~~~r=|b|$$となり、これらより円の方程式を求めます。$$~~~(x-a)^2+(y-b)^2=b^2$$
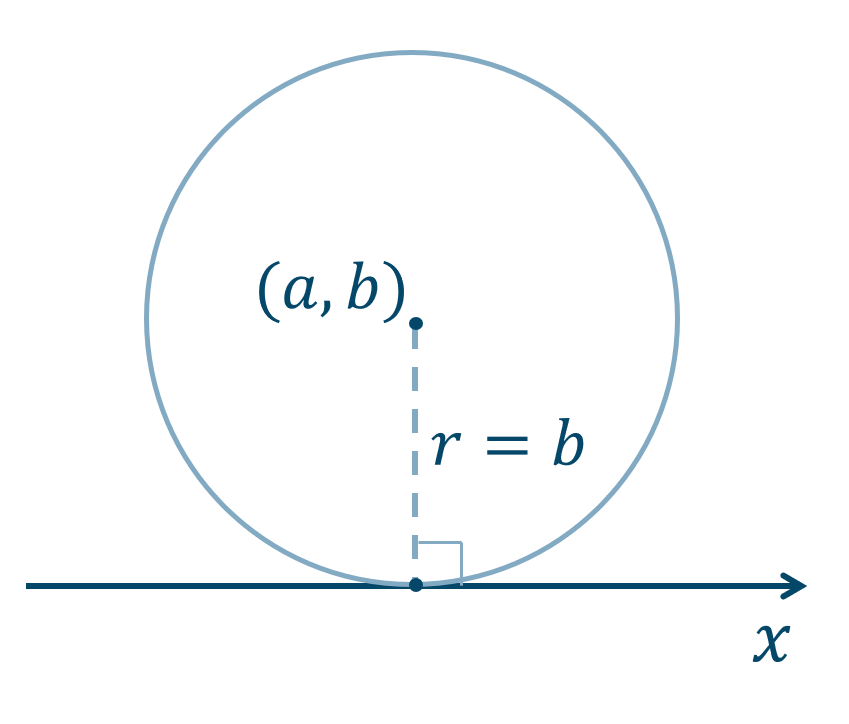
・\(y\) 軸と接する円
中心が \((a,b)\) ので \(y\) 軸と接するとき、中心の \(x\) 座標より半径は、$$~~~r=|a|$$となり、これらより円の方程式を求めます。$$~~~(x-a)^2+(y-b)^2=a^2$$
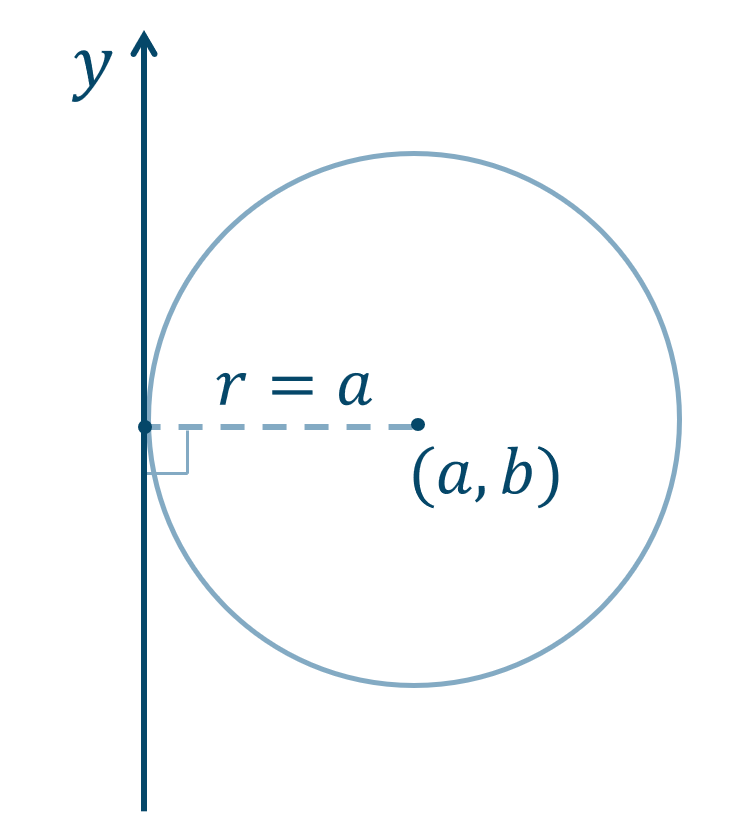
・直線に接する円
中心が \((p,q)\) で直線 \(ax+by+c=0\) に接する円の半径は、中心と直線との距離 \(d\) となります。$$~~~d=\frac{|ap+bq+c|}{\sqrt{a^2+b^2}}$$よって、求める円の方程式は、$$~~~(x-p)^2+(y-q)^2=d^2$$となります。
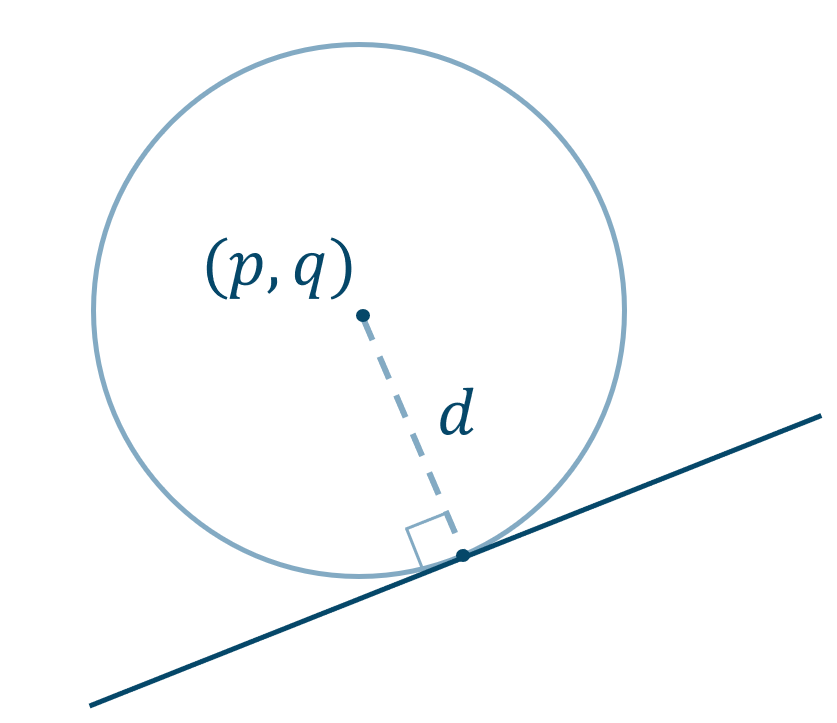
問題解説:円の方程式の決定②(接する条件)
問題解説(1)
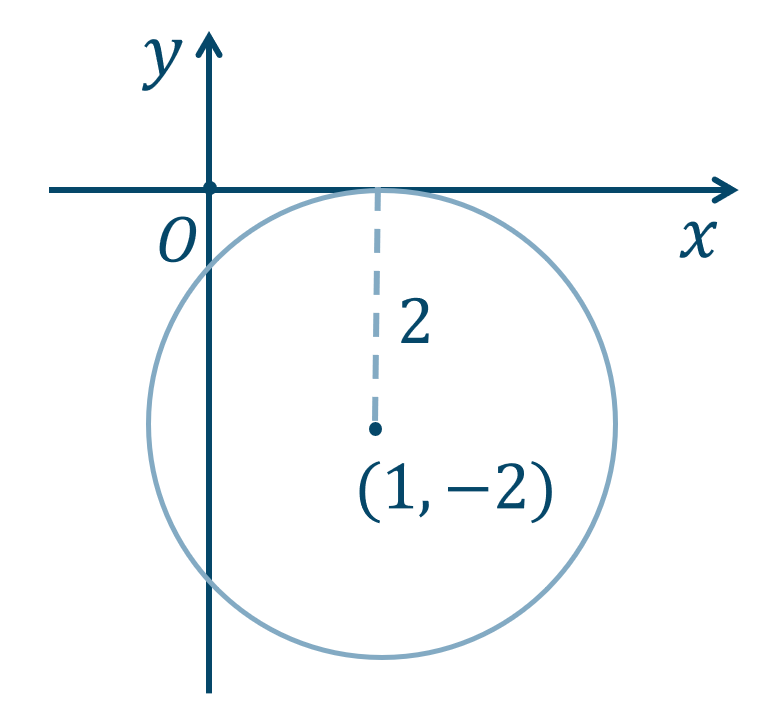
\({\small (1)}~\)点 \((1,-2)\) を中心として、\(x\) 軸に接する円
点 \((1,-2)\) が中心で \(x\) 軸と接する円となるので、
半径 \(r\) は、$$~~~r=|-2|=2$$これより、求める円の方程式は、$$~~~(x-1)^2+\{y-(-2)\}^2=2^2$$$$\hspace{ 26 pt} (x-1)^2+(y+2)^2=4$$よって、答えは \((x-1)^2+(y+2)^2=4\) となります。
問題解説(2)
\({\small (2)}~\)点 \((1,-2)\) を中心として、\(y\) 軸に接する円
点 \((1,-2)\) が中心で \(y\) 軸と接する円となるので、
半径 \(r\) は、$$~~~r=|1|=1$$これより、求める円の方程式は、$$~~~(x-1)^2+\{y-(-2)\}^2=1^2$$$$\hspace{ 26 pt} (x-1)^2+(y+2)^2=1$$よって、答えは \((x-1)^2+(y+2)^2=1\) となります。
問題解説(3)
\({\small (3)}~\)点 \((2,1)\) を中心として、直線 \(2x-y+2=0\) に接する円
点 \((2,1)\) が中心で、直線 \(2x-y+2=0\) に接する円になることより、
この円の半径は点と直線との距離の公式より、$$~~~d=\frac{|2\cdot2+-1\cdot1+2|}{\sqrt{2^2+(-1)^2}}$$$$\hspace{ 16 pt}=\frac{|4-1+2|}{\sqrt{4+1}}$$$$\hspace{ 16 pt}=\frac{|5|}{\sqrt{5}}$$$$\hspace{ 16 pt}=\frac{5}{\sqrt{5}}$$分母分子に \(\sqrt{5}\) をかけると、$$\hspace{ 16 pt}=\frac{5}{\sqrt{5}}\times\frac{\sqrt{5}}{\sqrt{5}}$$$$\hspace{ 16 pt}=\frac{5\sqrt{5}}{5}$$$$\hspace{ 16 pt}=\sqrt{5}$$これより、求める円の方程式は、$$~~~(x-2)^2+(y-1)^2=(\sqrt{5})^2$$$$~~~(x-2)^2+(y-1)^2=5$$よって、答えは \((x-2)^2+(y-1)^2=5\) となります。
今回のまとめ
直線と円が接する条件のときは、その位置関係より円の半径を求め、円の方程式を計算しましょう。