円と直線との位置関係の解法
直線の式に未知数がある場合はこちらの解法の方がおすすめです。
① 円と直線の方程式を連立して \(x\) の2次方程式をつくります。
② 2次方程式の判別式 \(D\) とすると、条件より、
( ⅰ ) 異なる2点で交わる
\(~\Leftrightarrow~\) \(D>0\)
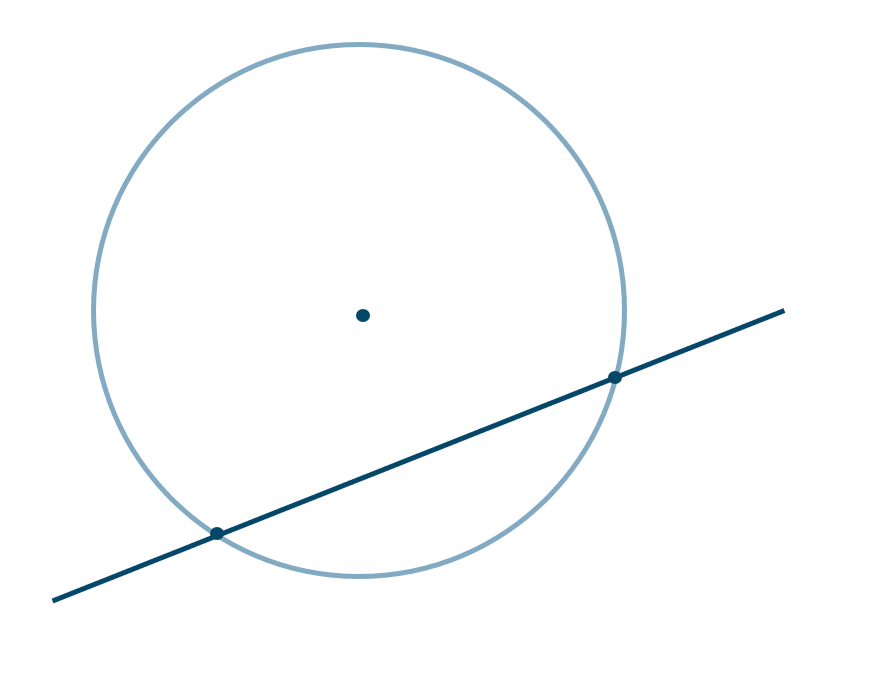
( ⅱ ) 接する
\(~\Leftrightarrow~\) \(D=0\)

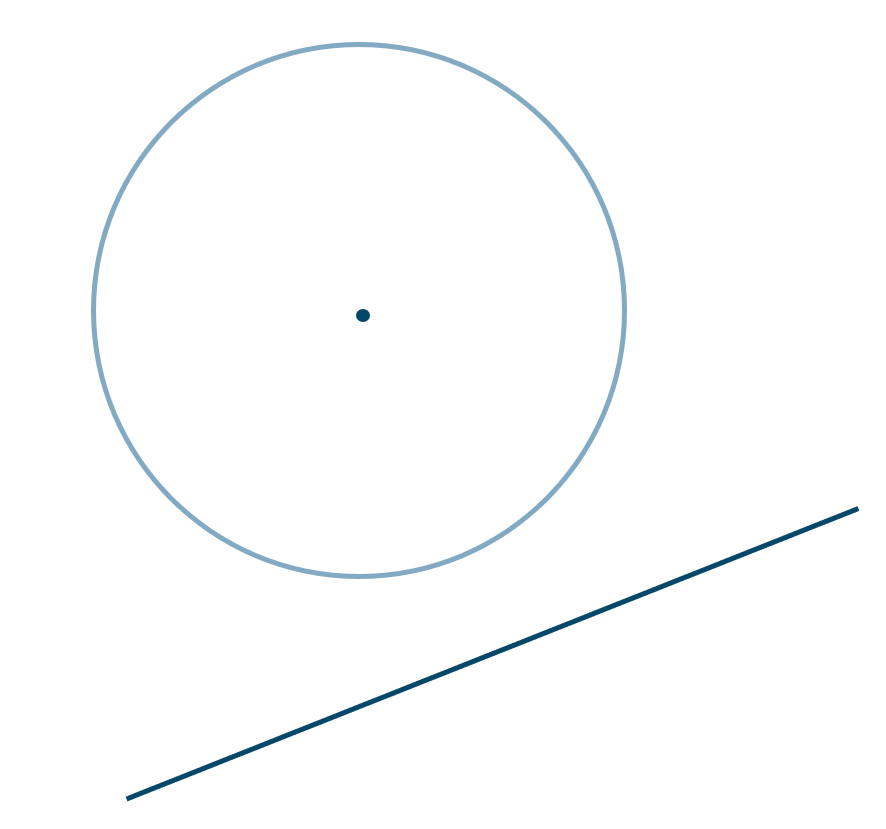
( ⅲ ) 共有点をもたない
\(~\Leftrightarrow~\) \(D<0\)
【解法パターン2】
円の半径が未知数となっている場合はこちら解法がおすすめです。
① 円の中心と直線との距離 \(d\) を求めます。
② 円の半径 \(r\) と比較すると、
( ⅰ ) 異なる2点で交わる
\(~\Leftrightarrow~\) \(d<r\)
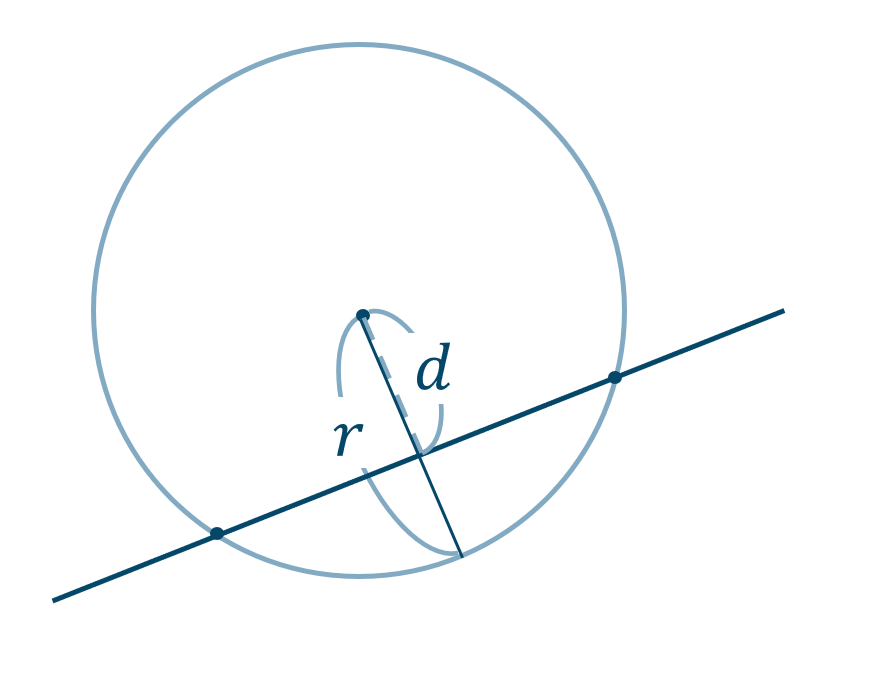
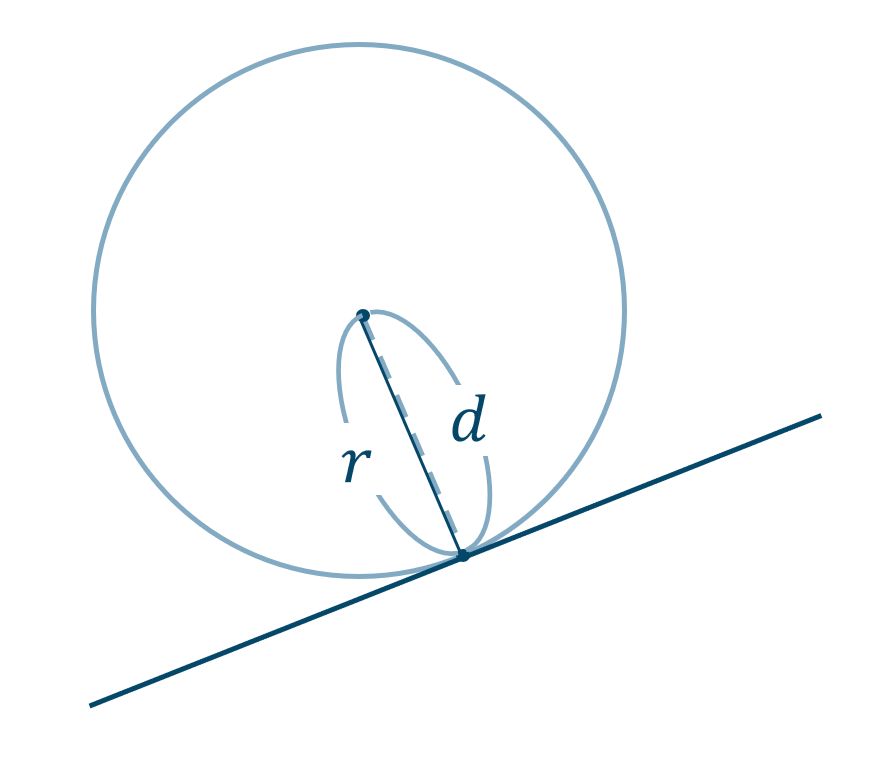
( ⅱ ) 接する
\(~\Leftrightarrow~\) \(d=r\)
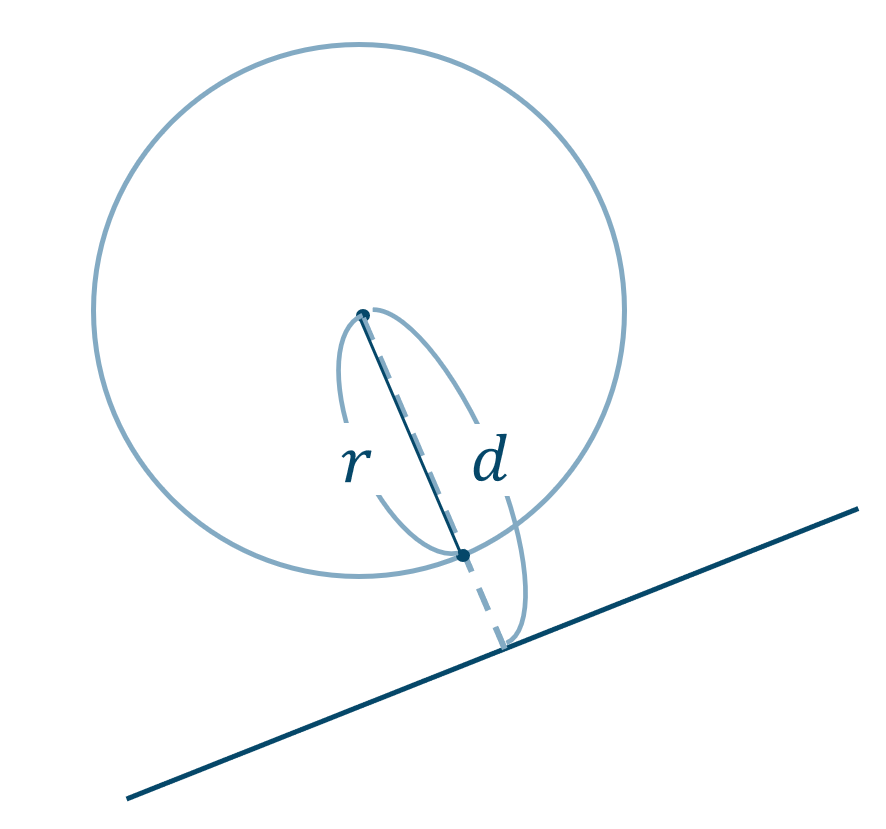
( ⅲ ) 共有点をもたない
\(~\Leftrightarrow~\) \(d>r\)
問題解説:円と直線との位置関係
問題解説(1)
\({\small (1)}~\)円 \(x^2+y^2=10\) と直線 \(y=3x+k\) が2点で交わるとき、実数 \(k\) の値の範囲を求めよ。
直線の方程式に未知数があるので解法パターン1を使って解きましょう。
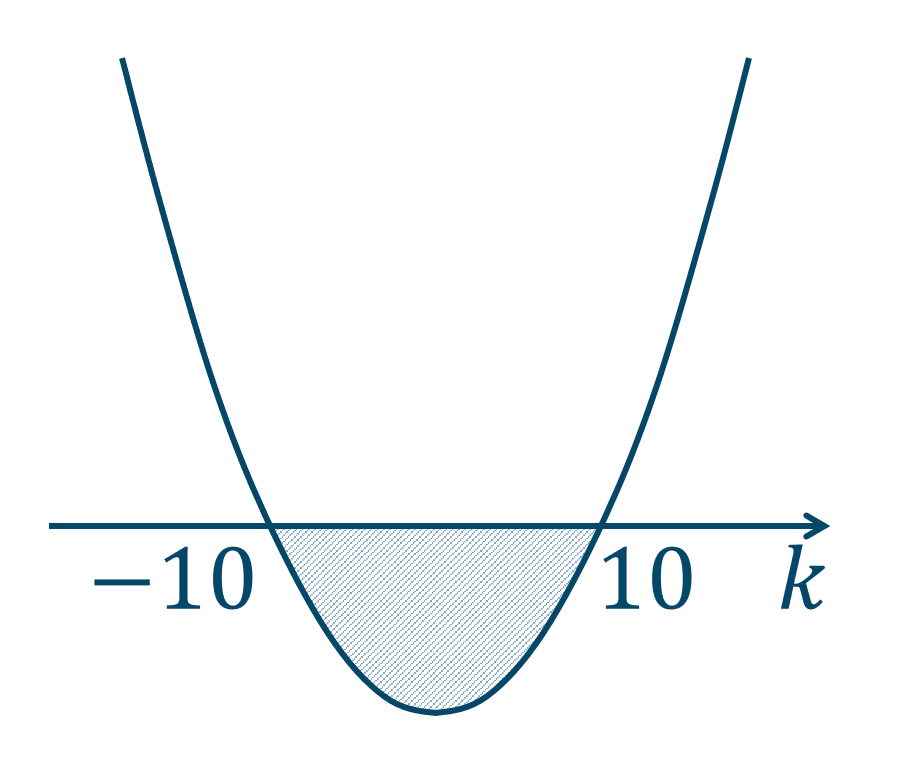
$$~~~\biggl\{ \begin{eqnarray} ~x^2+y^2-10=0~\cdots{\large ①} \\ ~y=3x+k~\cdots{\large ②}\end{eqnarray}$$②を①に代入すると、$$\hspace{35pt}x^2+(3x+k)^2-10=0$$$$\hspace{ 10 pt}x^2+9x^2+6kx+k^2-10=0$$$$\hspace{ 28 pt}10x^2+6kx+k^2-10=0$$この2次方程式の判別式を \(D\) とすると、$$~~~D=(6k)^2-4\cdot10\cdot(k^2-10)$$$$\hspace{ 18 pt}=36k^2-40k^2+400$$$$\hspace{ 18 pt}=-4k^2+400$$異なる2点で交わる条件より、\(D>0\) となるので、$$~~~-4k^2+400>0$$両辺を \(-4\) で割ると、不等号の向きが逆になるので、$$\hspace{ 45 pt}k^2-100<0$$$$\hspace{ 10 pt}(k+10)(k-10)<0$$
よって、答えはグラフより、\(-10<k<10\)となります。
問題解説(2)
\({\small (2)}~\)円 \(x^2+y^2=r^2\) と直線 \(y=-2x+1\) が接するとき、実数 \(r\) の値を求めよ。
円の半径が未知数となっているので解法パターン2で解きましょう。
直線の方程式を式変形すると、$$\hspace{ 10 pt}y=-2x+1$$$$\hspace{ 10 pt}2x+y-1=0$$となります。
よって、円 \(x^2+y^2=r^2\) の中心 \((0,0)\) と直線 \(2x+y-1=0\) との距離 \(d\) は、$$~~~d=\frac{|2\cdot0+0-1|}{\sqrt{2^2+1^2}}$$$$\hspace{ 16 pt}=\frac{|-1|}{\sqrt{4+1}}$$$$\hspace{ 16 pt}=\frac{1}{\sqrt{5}}$$分母分子に \(\sqrt{5}\) をかけると、$$\hspace{ 16 pt}=\frac{1}{\sqrt{5}}\times\frac{\sqrt{5}}{\sqrt{5}}$$$$\hspace{ 16 pt}=\frac{\sqrt{5}}{5}$$また、円 \(x^2+y^2=r^2\) の半径は \(r\) であり、円と直線が接する条件より、\(r=d\) となるので、$$~~~r=\frac{\sqrt{5}}{5}$$よって、答えは \({\Large \frac{\sqrt{5}}{5}}\) となります。
今回のまとめ
円と直線との位置関係の条件の方問題は、未知数の種類によって解法のパターンも選択しましょう。