円によって切り取られる線分の解法
① 円の中心と直線との距離 \(d\) を求めます。
② 求める弦の長さを \(x\) として、円の半径が \(r\) であることより、三平方の定理を用いて、\(x\) の値を求めます。
問題解説:円によって切り取られる線分
円 \(x^2+y^2=4\) の中心は \((0,0)\)で半径が \(r=2\) となります。
点 \((0,0)\) と直線 \(x-y-1=0\) との距離 \(d\) は、$$~~~d=\frac{|0-0-1|}{\sqrt{1^2+(-1)^2}}$$$$\hspace{ 16 pt}=\frac{|-1|}{\sqrt{1+1}}$$$$\hspace{ 16 pt}=\frac{1}{\sqrt{2}}$$分母分子に \(\sqrt{2}\) をかけると、$$\hspace{ 16 pt}=\frac{1}{\sqrt{2}}\times\frac{\sqrt{2}}{\sqrt{2}}$$$$\hspace{ 16 pt}=\frac{\sqrt{2}}{2}$$求める弦の長さを \(x\) として、次の図より三平方の定理を用いると、
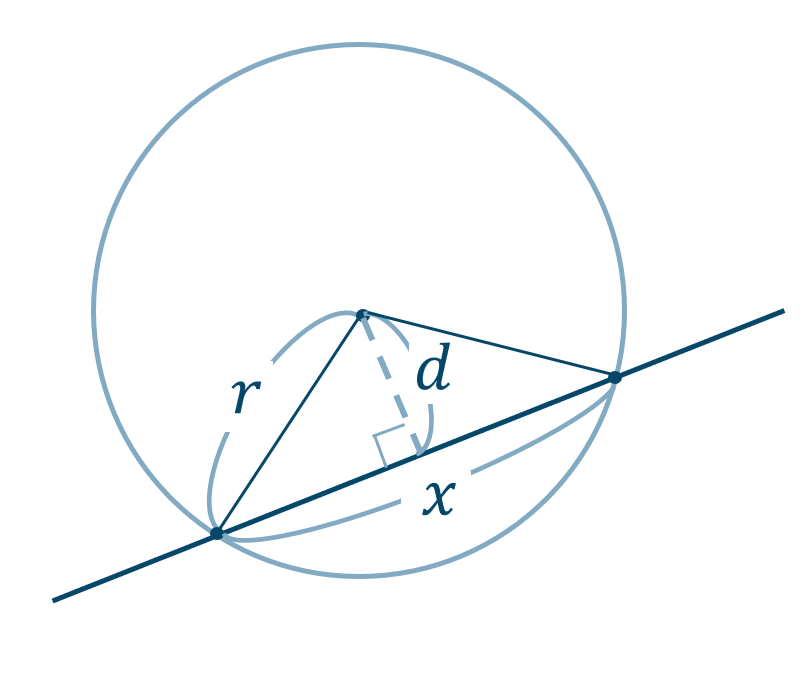
$$~~~r^2=\left(\frac{x}{2}\right)^2+d^2$$よって、値を代入すると、$$\hspace{ 10 pt}2^2=\left(\frac{x}{2}\right)^2+\left(\frac{\sqrt{2}}{2}\right)^2$$$$\hspace{ 14 pt}4=\frac{x^2}{4}+\frac{2}{4}$$両辺に \(4\) をかけると、$$\hspace{ 10 pt}16=x^2+2$$両辺を入れ替えると、$$\hspace{ 10 pt}x^2+2=16$$右辺に \(2\) を移項すると、$$\hspace{ 10 pt}x^2=16-2$$$$\hspace{ 10 pt}x^2=14$$\(x>0\) より、$$\hspace{ 10 pt}x=\sqrt{14}$$よって、答えは \(\sqrt{14}\) となります。
今回のまとめ
直線が円によって切り取られる線分の長さは、円の中心と直線の距離と円の半径を用いて三平方の定理より求めましょう。




