動径と一般角

2018.05.182020.06.09

動径と一般角の求め方

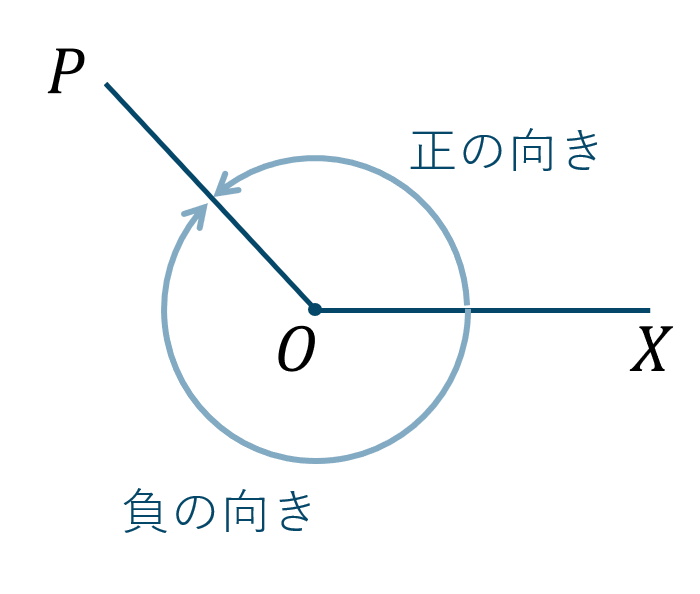
Point：動径次の図で $OX$ を「始線」、$OP$ を「動径」といい、反時計回りを「正の向き」、時計回りを「負の向き」といいます。

Point：一般角

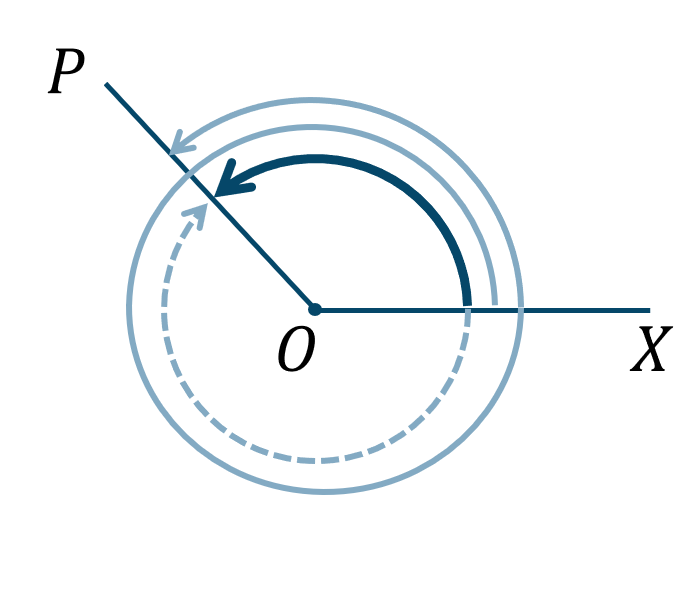
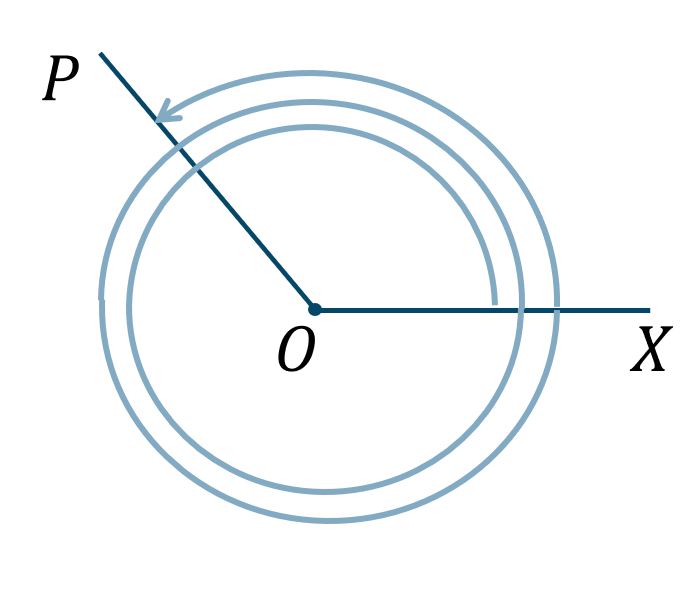
この図のように同じ位置にくるまで何周していても、逆向きであっても同じ動径 $OP$ を表します。このとき、動径 $OP$ を表す１つの角を $\alpha$ とするとき、動径 $OP$ の一般角は次のようになります。

$$\alpha+360^\circ \times n~~~(n=0~,~\pm1~,~\pm2~,~\cdots~)$$

問題次の角の動径を図示せよ。また、この角の動径を表す最小の正の角を求めよ。$${\small (1)}~400^\circ$$

$$~~~400^\circ=40^\circ +360^\circ \times 1$$よって１周して正の向きに $40^\circ$ 進むので、

また、この動径の最小の正の角は $40^\circ$ となります。

問題次の角の動径を図示せよ。また、この角の動径を表す最小の正の角を求めよ。$${\small (2)}~850^\circ$$

$$~~~850^\circ=130^\circ +360^\circ \times 2$$よって２周して正の向きに $130^\circ$ 進むので、

また、この動径の最小の正の角は $130^\circ$ となります。

問題次の角の動径を図示せよ。また、この角の動径を表す最小の正の角を求めよ。$${\small (3)}~-600^\circ$$

$$~~~-600^\circ=120^\circ +360^\circ \times (-2)$$よって負の向きに１周して負の向きに $360^\circ-120^\circ=240^\circ $ 進むので、

また、この動径の最小の正の角は $120^\circ$ となります。

動径についての問題は一般角で表すことができるようになりましょう。また、正の向きと負の向きに注意しましょう。