三角関数のグラフ
また、この定数 \(p\) の値の正の最小の値を「周期」といいます。
関数 \(f(x)\) において、
① 常に \(f(-x)=-f(x)\) が成り立つ
\(~\Leftrightarrow~f(x)\) が奇関数
奇関数は原点対称のグラフとなります。
② 常に \(f(-x)=f(x)\) が成り立つ
\(~\Leftrightarrow~f(x)\) が偶関数
偶関数は \(y\) 軸対称のグラフとなります。
① \(y=\sin{\theta}\) のグラフ
この関数の周期は \(2\pi\) となります。
また、この関数は奇関数となります。
② \(y=\cos{\theta}\) のグラフ
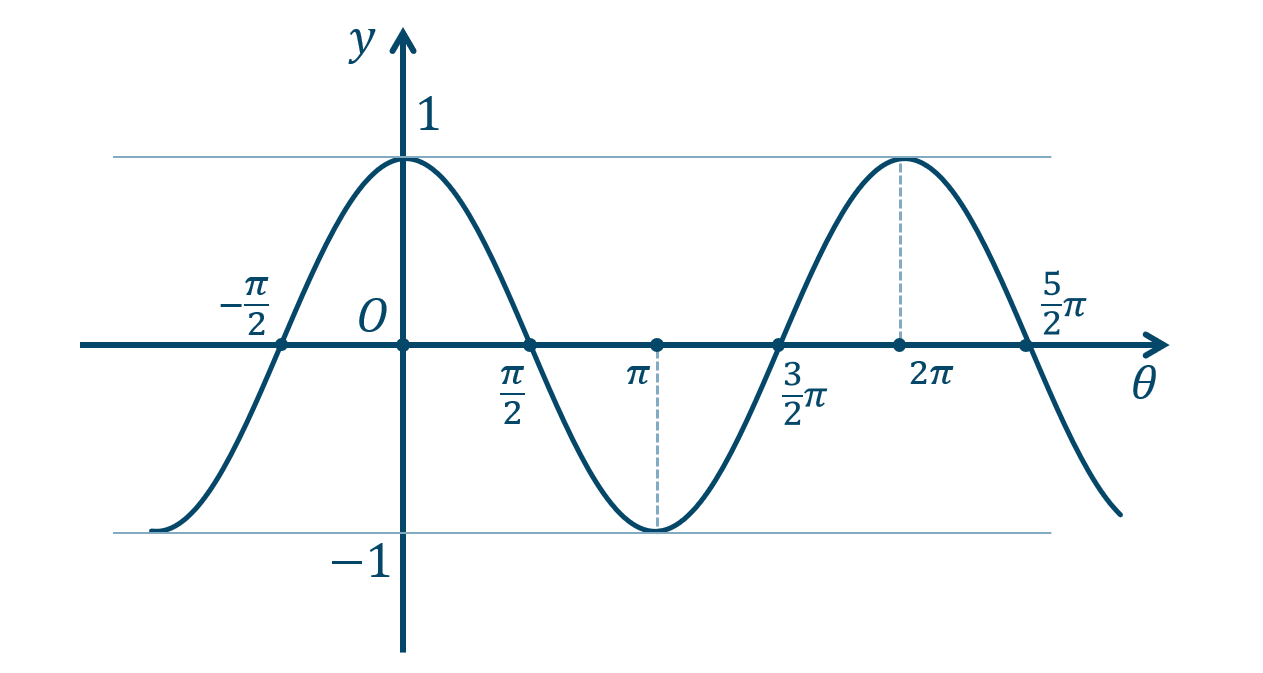
この関数の周期は \(2\pi\) となります。
また、この関数は偶関数となります。
③ \(y=\tan{\theta}\) のグラフ
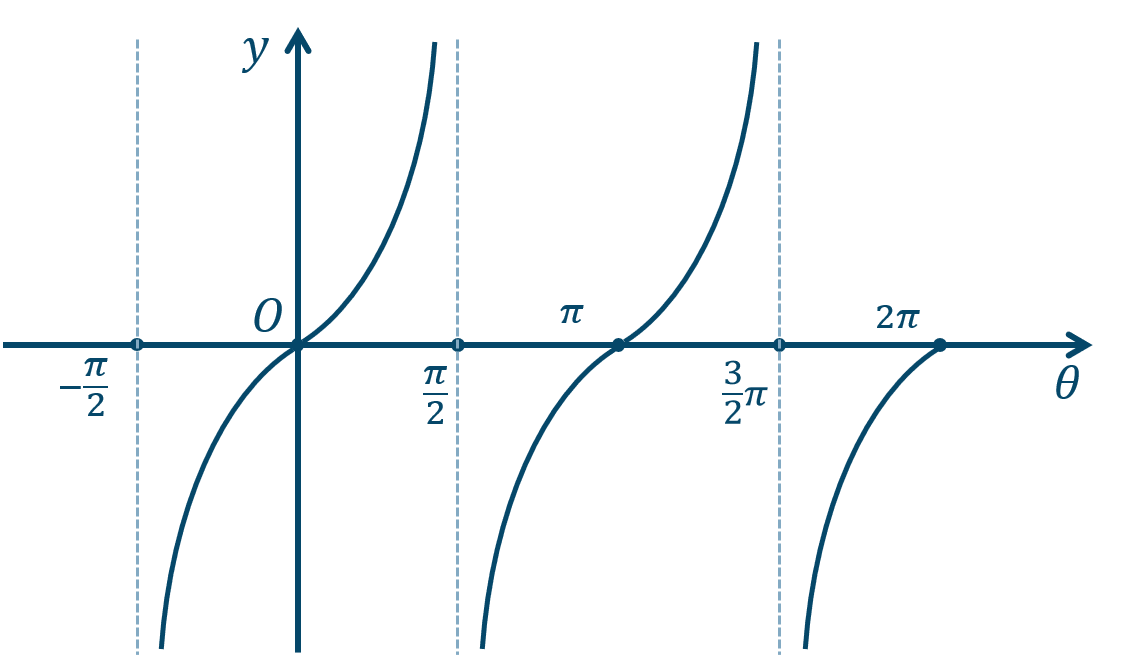
この関数の周期は \(\pi\) となります。
また、この関数は奇関数となります。
定義域は、$$~~~\theta=\frac{\pi}{2}+n\pi~~(n=0~,~\pm1~,~\pm2~,~\cdots)$$を除く実数全体となります。
また、次の直線が漸近線となります。$$~~~\theta=\frac{\pi}{2}+n\pi~~(n=0~,~\pm1~,~\pm2~,~\cdots)$$
問題解説:三角関数のグラフ①
問題解説(1)
① 通る点などを書き込んでいきます。
\(\theta\) 軸上の点は、$$~~~0~,~\pi~,~2\pi~,~\cdots$$また、\(y=\pm1\) となる点は、$$~~~-\frac{\pi}{2}~,~\frac{\pi}{2}~,~\frac{3}{2}\pi~,~\cdots$$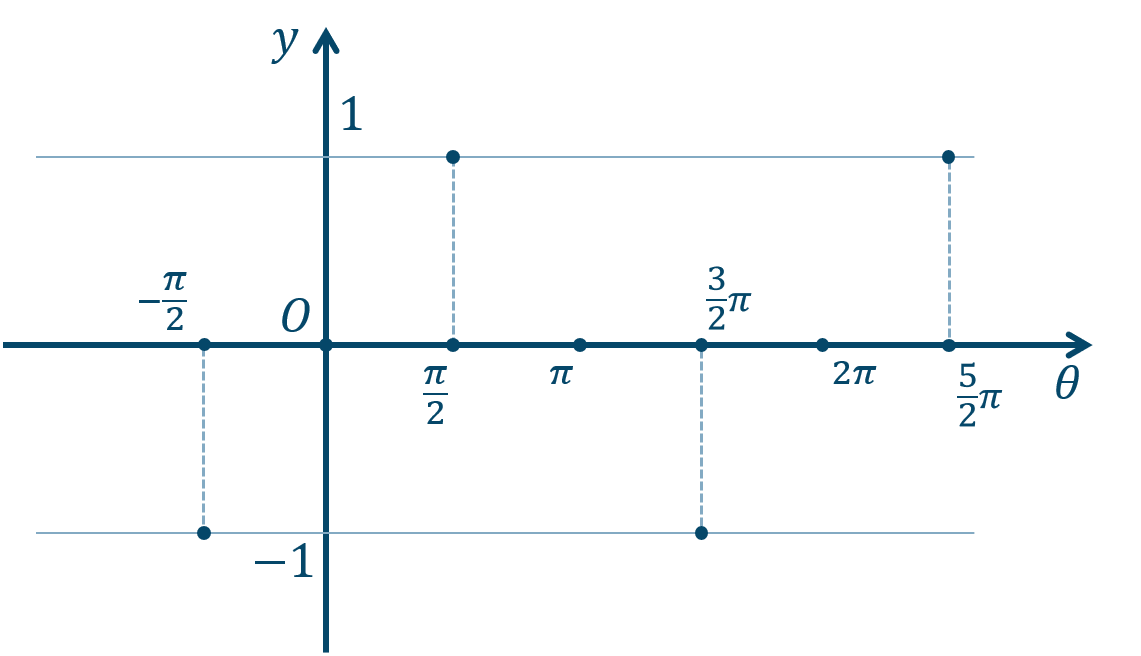
② 点を曲線で結びます。また、点の座標や、\(y=\pm1\) の線を書き込みます。
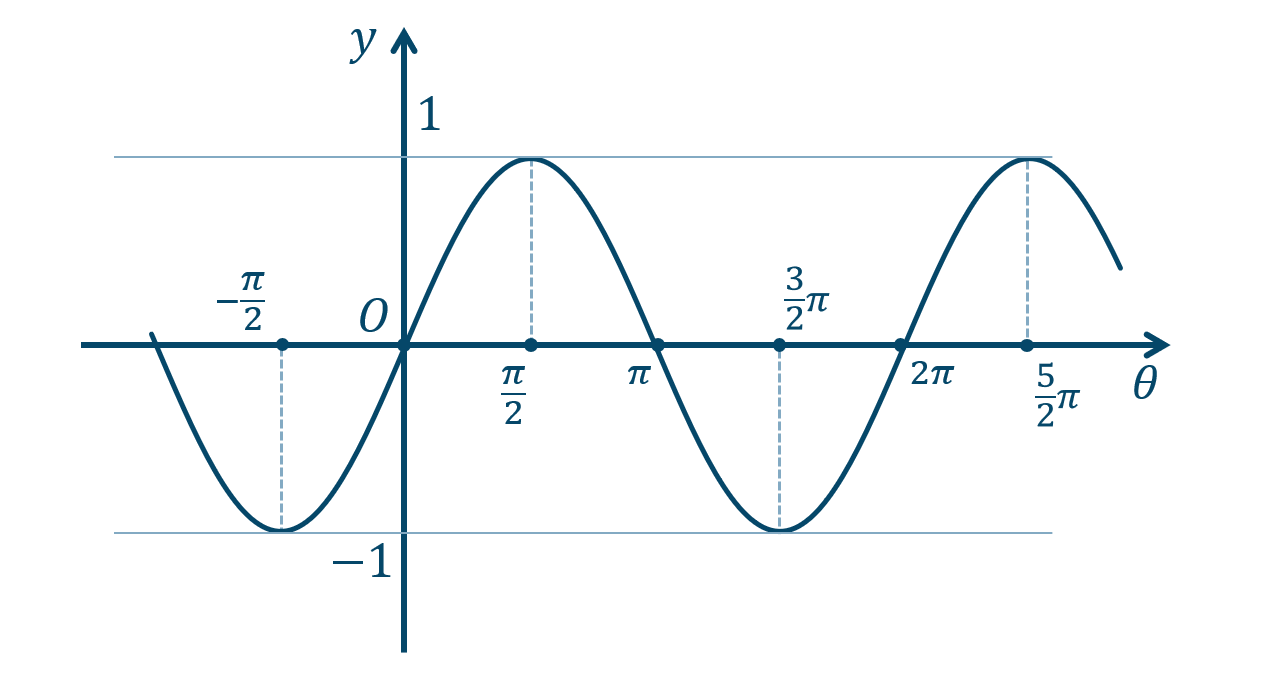
また、この関数の周期は \(2\pi\) となります。
問題解説(2)
① 通る点などを書き込んでいきます。
\(\theta\) 軸上の点は、$$~~~-\frac{\pi}{2}~,~\frac{\pi}{2}~,~\frac{3}{2}\pi~,~\cdots$$また、\(y=\pm1\) となる点は、$$~~~0~,~\pi~,~2\pi~,~\cdots$$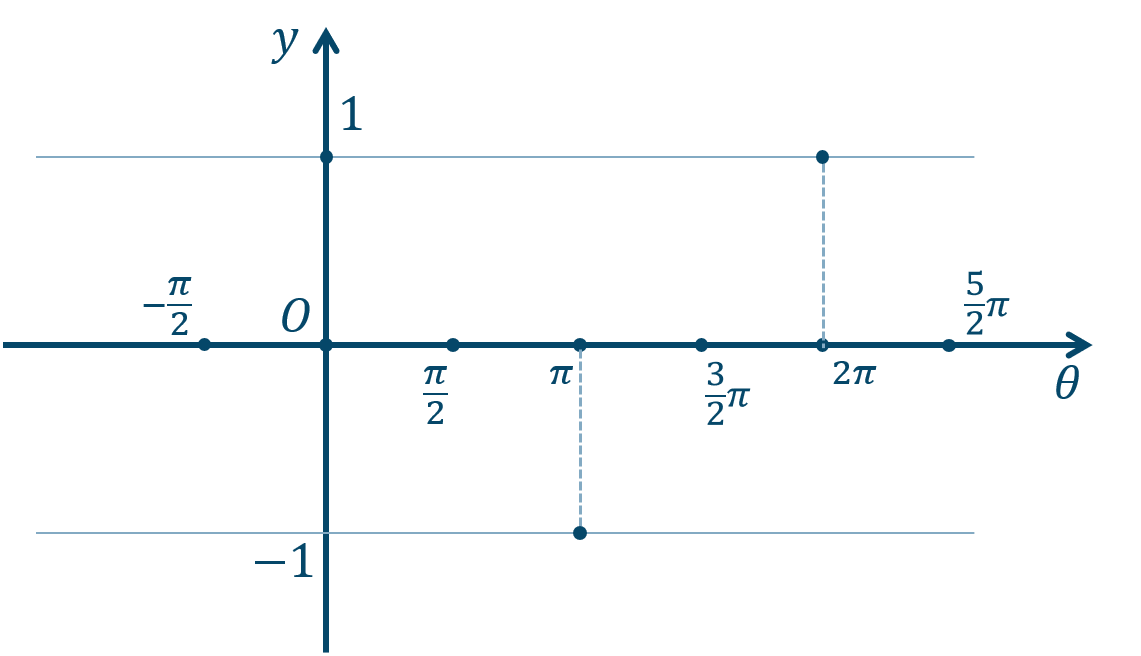
② 点を曲線で結びます。また、点の座標や、\(y=\pm1\) の線を書き込みます。

また、この関数の周期は \(2\pi\) となります。
問題解説(3)
① 通る点と漸近線を書き込んでいきます。
通る点は、$$~~~0~,~\pi~,~2\pi~,~\cdots$$また、漸近線の位置は、$$~~~-\frac{\pi}2~,~\frac{\pi}{2}~,~\frac{3}{2}\pi~,~\cdots$$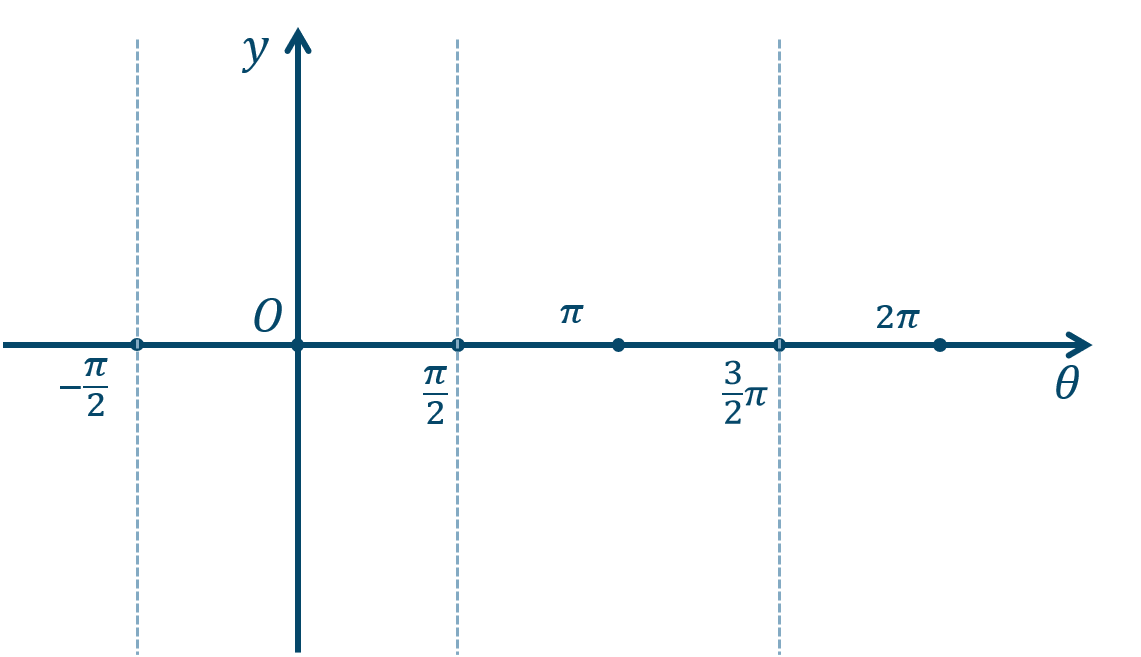
② 点を曲線で結んで、漸近線に近づくようにグラフを描きます。また、点の座標を書き込みます。

また、この関数の周期は \(\pi\) となります。
今回のまとめ
三角関数のグラフは、それぞれ通る点や漸近線などを書き込んで、その点を結んでグラフを描くようにしましょう。




