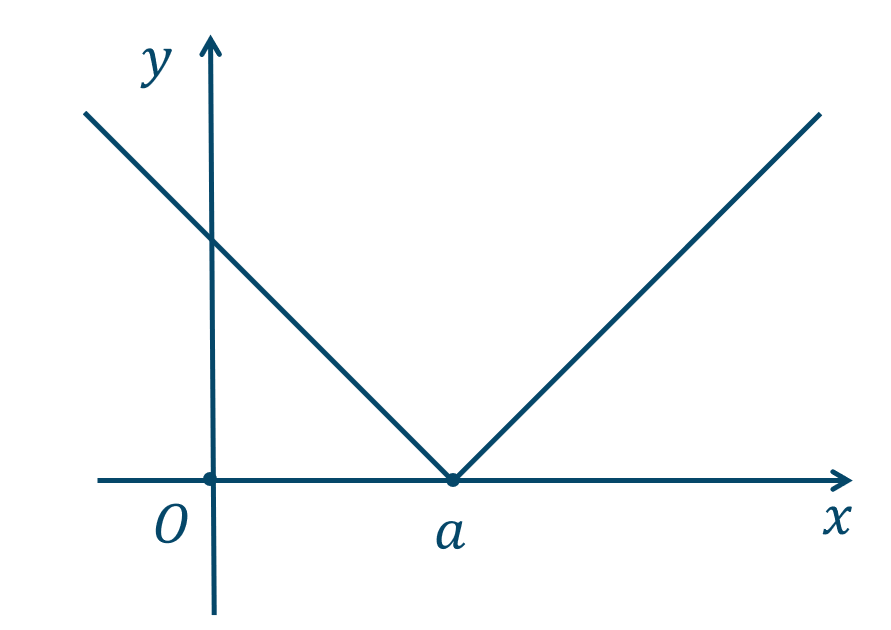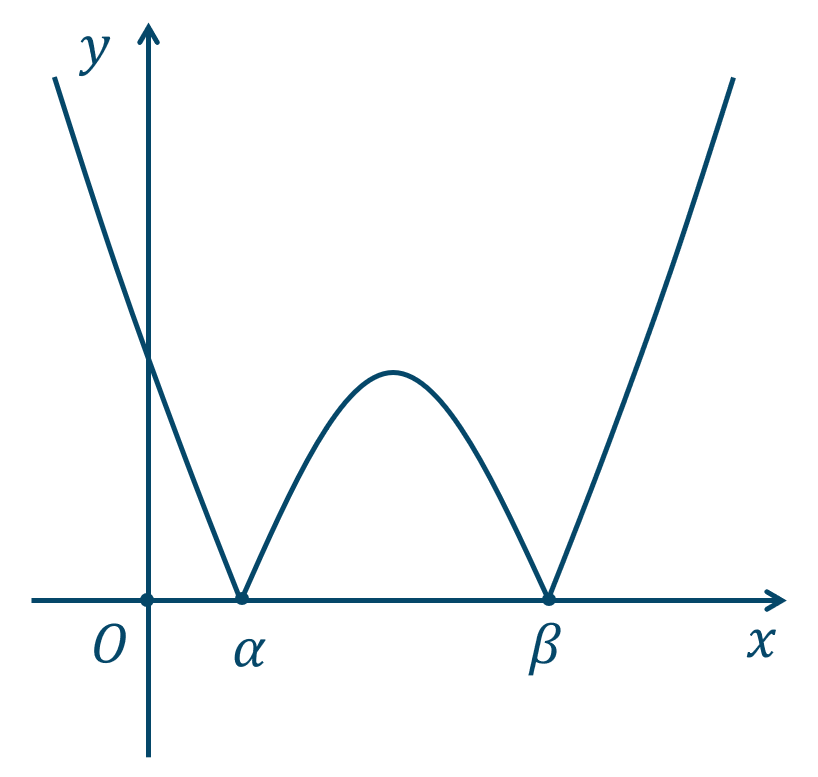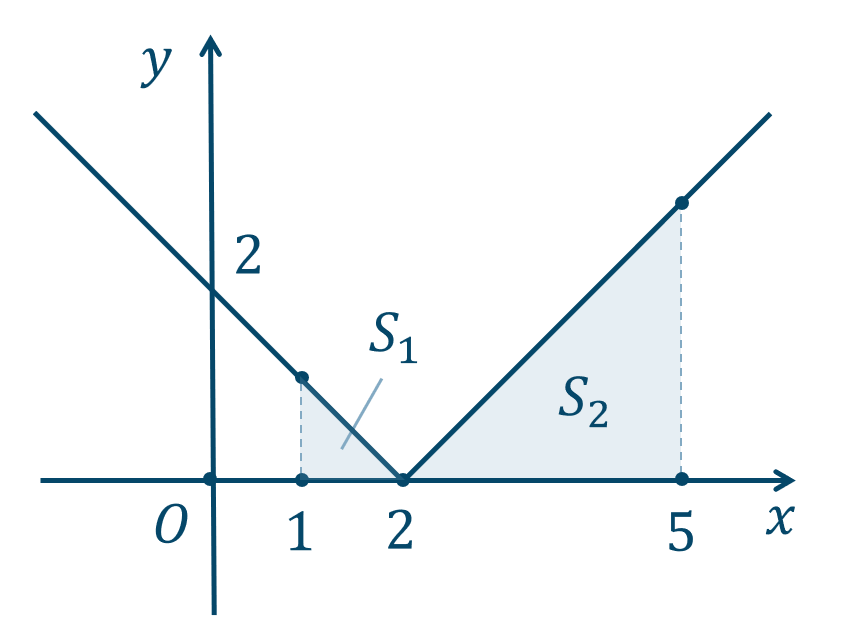絶対値を含む関数の定積分の解法
② グラフより、区間に分けてそれぞれで積分計算をします。
(1) \(y=|x-a|\)
( ⅰ ) \(x≧a\) のとき、$$~~~y=x-a$$( ⅱ ) \(x<a\) のとき、$$~~~y=-x+a$$
(2) \(y=|(x-\alpha)(x-\beta)|\)
( ⅰ ) \(x≦\alpha~,~\beta≦x\) のとき、$$~~~y=(x-\alpha)(x-\beta)$$( ⅱ ) \(\alpha<x<\beta\) のとき、$$~~~y=-(x-\alpha)(x-\beta)$$
問題解説:絶対値を含む関数の定積分
問題解説(1)
関数 \(y=|x-2|\) のグラフは、
( ⅰ ) \(x-2≧0\) すなわち \(x≧2\) のとき、$$~~~y=x-2$$( ⅱ ) \(x-2<0\) すなわち \(x<2\) のとき、$$~~~y=-x+2$$
よって、グラフは
区間 \(1\) 〜 \(2\) の部分の面積 \(S_1\) は、$$~~~~~~\int_{1}^{2} (-x+2) dx$$$$~=\left[ -\frac{1}{2}x^2+2x \right]_{1}^{2}~~~\cdots{\large ①}$$
ここで、①の [ ] の中の関数に \(x=2\) を代入した値は、$$~~~~~~-\frac{1}{2}\cdot2^2+2\cdot2$$$$~=-2+4$$$$~=2$$
また、\(x=1\) を代入した値は、$$~~~~~~-\frac{1}{2}\cdot1^2+2\cdot1$$$$~=-\frac{1}{2}+2$$$$~=\frac{-1+4}{2}$$$$~=\frac{3}{2}$$
よって、①の計算の続きは、$$~~~~~~\left[ -\frac{1}{2}x^2+2x \right]_{1}^{2}$$$$~=2-\frac{3}{2}$$$$~=\frac{4-3}{2}$$$$~=\frac{1}{2}$$
次に、区間 \(2\) 〜 \(5\) の部分の面積 \(S_2\) は、$$~~~~~~\int_{2}^{5}(x-2)dx$$$$~=\left[ \frac{1}{2}x^2-2x \right]_{2}^{5}~~~\cdots{\large ②}$$
ここで、②の [ ] の中の関数に \(x=5\) を代入した値は、$$~~~~~~\frac{1}{2}\cdot5^2-2\cdot5$$$$~=\frac{25}{2}-10$$$$~=\frac{25-20}{2}$$$$~=\frac{5}{2}$$
また、\(x=2\) を代入した値は、$$~~~~~~\frac{1}{2}\cdot2^2-2\cdot2$$$$~=2-4$$$$~=-2$$
よって、②の計算の続きは、$$~~~~~~\left[ \frac{1}{2}x^2-2x \right]_{2}^{5}$$$$~=\frac{5}{2}-(-2)$$$$~=\frac{5}{2}+2$$$$~=\frac{5+4}{2}$$$$~=\frac{9}{2}$$
したがって、求める面積 \(S_1+S_2\) は、$$~~~~~~\frac{1}{2}+\frac{9}{2}$$$$~=\frac{10}{2}$$$$~=5$$
よって、答えは \(5\) となります。
問題解説(2)
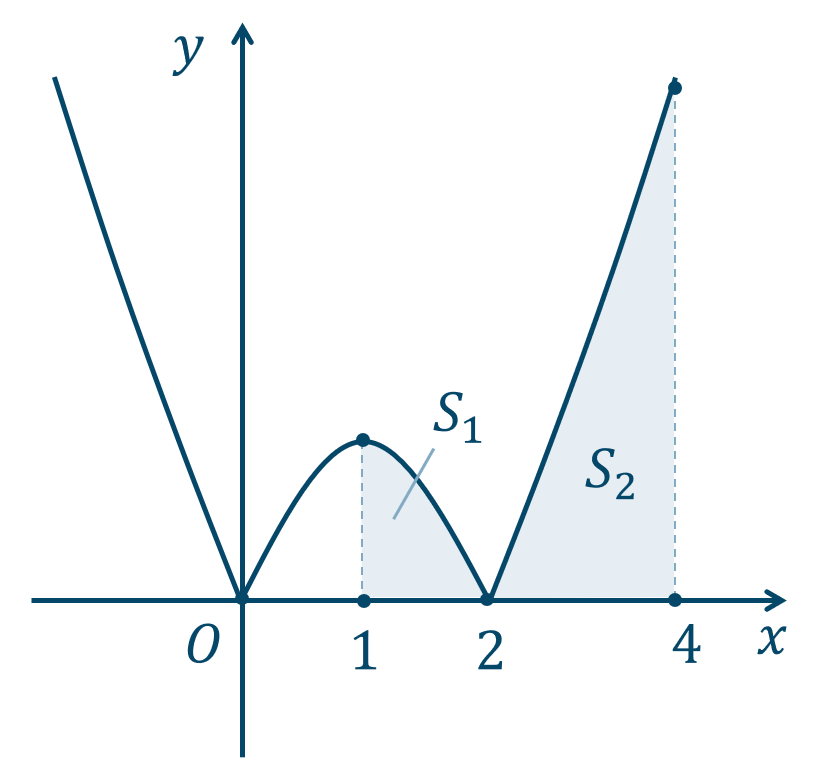
関数 \(y=|x^2-2x|\) のグラフは、
( ⅰ ) \(x^2-2x≧0\) のとき、すなわち \(x≦0~,~2≦x\) のとき、$$~~~y=x^2-2x$$( ⅱ ) \(x^2-2x<0\) のとき、すなわち \(0<x<2\) のとき、$$~~~y=-x^2+2x$$
よって、グラフは
区間 \(1\) 〜 \(2\) の部分の面積 \(S_1\) は、$$~~~~~~\int_{1}^{2}(-x^2+2x)dx$$$$~=\left[ -\frac{1}{3}x^3+x^2 \right]_{1}^{2}~~~\cdots{\large ①}$$
ここで、①の [ ] の中の関数に \(x=2\) を代入した値は、$$~~~~~~-\frac{1}{3}\cdot2^3+2^2$$$$~=-\frac{8}{3}+4$$$$~=\frac{-8+12}{3}$$$$~=\frac{4}{3}$$
また、\(x=1\) を代入した値は、$$~~~~~~-\frac{1}{3}\cdot1^3+1^2$$$$~=-\frac{1}{3}+1$$$$~=\frac{-1+3}{3}$$$$~=\frac{2}{3}$$
よって、①の計算の続きは、$$~~~~~~\left[ -\frac{1}{3}x^3+x^2 \right]_{1}^{2}$$$$~=\frac{4}{3}-\frac{2}{3}$$$$~=\frac{2}{3}$$
次に、区間 \(2\) 〜 \(4\) の部分の面積 \(S_2\) は、$$~~~~~~\int_{2}^{4}(x^2-2x)dx$$$$~=\left[ \frac{1}{3}x^3-x^2 \right]_{2}^{4}~~~\cdots{\large ②}$$
ここで、②の [ ] の中の関数に \(x=4\) を代入した値は、$$~~~~~~\frac{1}{3}\cdot4^3-4^2$$$$~=\frac{64}{3}-16$$$$~=\frac{64-48}{3}$$$$~=\frac{16}{3}$$
また、\(x=2\) を代入した値は、$$~~~~~~\frac{1}{3}\cdot2^3-2^2$$$$~=\frac{8}{3}-4$$$$~=\frac{8-12}{3}$$$$~=-\frac{4}{3}$$
よって、②の計算の続きは、$$~~~~~~\left[ \frac{1}{3}x^3-x^2 \right]_{2}^{4}$$$$~=\frac{16}{3}-\left( -\frac{4}{3} \right)$$$$~=\frac{16}{3}+\frac{4}{3}$$$$~=\frac{20}{3}$$
したがって、求める面積 \(S_1+S_2\) は、$$~~~~~~\frac{2}{3}+\frac{20}{3}$$$$~=\frac{22}{3}$$
よって、答えは$$~~~\frac{22}{3}$$となります。
今回のまとめ
絶対値を含む関数の定積分は、場合分けが必要となるのでまずはグラフを描いて区間での変化を確認しましょう。