無理関数の極限の解法
分子を有理化すると解消できることが多いです。
分母の最高次数の項で、分母分子のすべての項を割ると解消できることが多いです。
分母または分子を有理化すると解消できることが多いです。
\(x\to-\infty\) となっている極限はそのままでは考えにくいです。
よって、\(t=-x\) と置き換えることにより、\(t\to\infty\) と正の無限大で考えることができます。
問題解説:無理関数の極限①
問題解説(1)
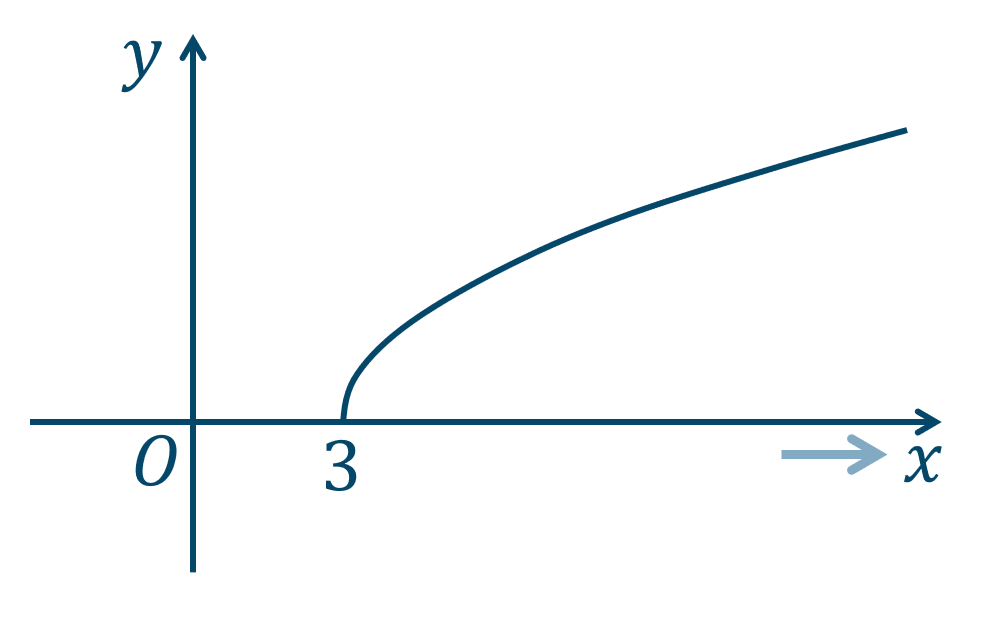
\(y=\sqrt{x-3}\) のグラフは次のようになります。
したがって、$$~~~\lim_{x\to\infty}\sqrt{x-3}=\infty$$よって、答えは \(\infty\) となります。
問題解説(2)
$$~~~~~~\lim_{x\to\infty}(\sqrt{x^2+2}-x)$$このままだと、\(\infty-\infty\) の不定形となります。
分母分子に \(\sqrt{x^2+2}+x\) をかけると、$$~=\lim_{x\to\infty}(\sqrt{x^2+2}-x)\times\frac{\sqrt{x^2+2}+x}{\sqrt{x^2+2}+x}$$$$~=\lim_{x\to\infty}\frac{(\sqrt{x^2+2})^2-x^2}{\sqrt{x^2+2}+x}$$$$~=\lim_{x\to\infty}\frac{(x^2+2)-x^2}{\sqrt{x^2+2}+x}$$$$~=\lim_{x\to\infty}\frac{2}{\sqrt{x^2+2}+x}$$\(x\to\infty\) のとき、\(\sqrt{x^2+2}+x\to\infty\) となるので、$$~=0$$よって、答えは \(0\) となります。
問題解説(3)
$$~~~~~~\lim_{x\to-\infty}(\sqrt{x^2-3x}+x)$$\(t=-x\) と置き換えると、\(t\to\infty\) となります。よって、与式は、$$~~~~~~\lim_{t\to\infty}\{\sqrt{(-t)^2-3(-t)}+(-t)\}$$$$~=\lim_{t\to\infty}(\sqrt{t^2+3t}-t)$$このままだと、\(\infty-\infty\) の不定形となります。
分母分子に \(\sqrt{t^2+3t}+t\) をかけると、$$~=\lim_{t\to\infty}(\sqrt{t^2+3t}-t)\times\frac{\sqrt{t^2+3t}+t}{\sqrt{t^2+3t}+t}$$$$~=\lim_{t\to\infty}\frac{(\sqrt{t^2+3t})^2-t^2}{\sqrt{t^2+3t}+t}$$$$~=\lim_{t\to\infty}\frac{t^2+3t-t^2}{\sqrt{t^2+3t}+t}$$$$~=\lim_{t\to\infty}\frac{3t}{\sqrt{t^2+3t}+t}$$このままだと、\({\Large \frac{\infty}{\infty}}\) の不定形となります。
分母の最大次数の項 \(t\) で分母分子のすべての項を割ると、$$~=\lim_{t\to\infty}\frac{{\Large \frac{3t}{t}}}{{\Large \frac{\sqrt{t^2+3t}}{t}}+{\Large \frac{t}{t}}}$$$$~=\lim_{t\to\infty}\frac{3}{\sqrt{{\Large \frac{t^2+3t}{t^2}}}+1}$$$$~=\lim_{t\to\infty}\frac{3}{\sqrt{1+{\Large \frac{3}{t}}}+1}$$\(t\to\infty\) のとき、\({\Large \frac{1}{t}}\to 0\) となるので、$$~=\frac{3}{\sqrt{1+0}+1}$$$$~=\frac{3}{1+1}$$$$~=\frac{3}{2}$$よって、答えは \({\Large \frac{3}{2}}\) となります。
今回のまとめ
無理関数の極限はでは、分子を有理化する解法を覚えておきましょう。また、\(x\to-\infty\) は置き換えを用いて計算しましょう。