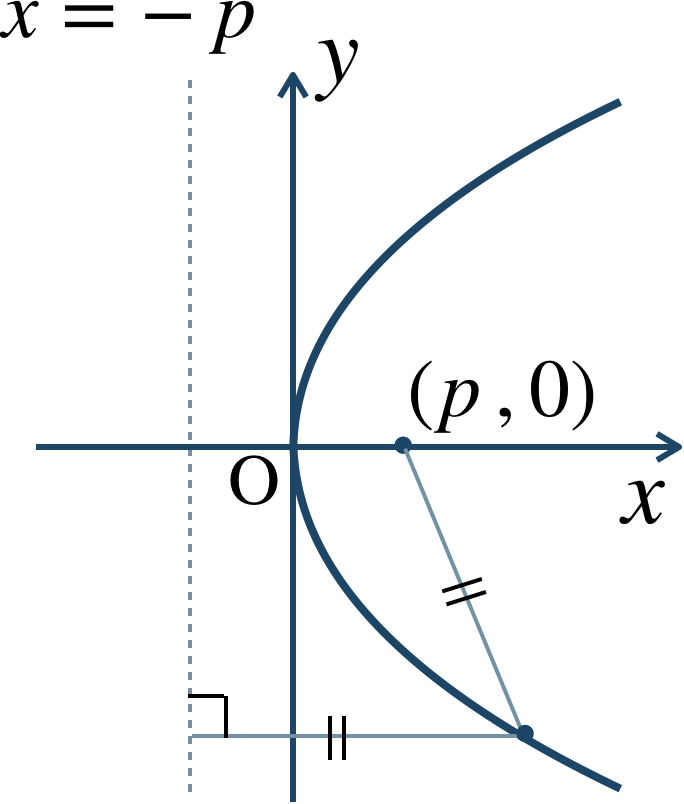放物線の標準形の解法
■ \(x\) 軸が軸の放物線
焦点 \((p~,~0)\) 、準線 \(x=-p\) の放物線は、
頂点は原点 \((0~,~0)\) である。
\(x\) 軸( \(y=0\) )が軸で、\(x\) 軸で対称となる。
概形は、
(ⅰ) \(p\gt0\) のとき、
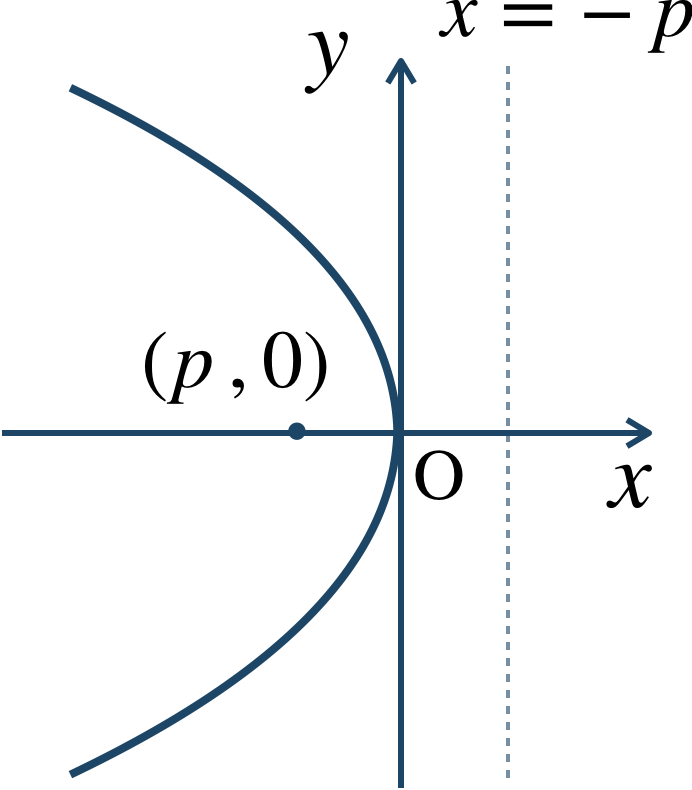
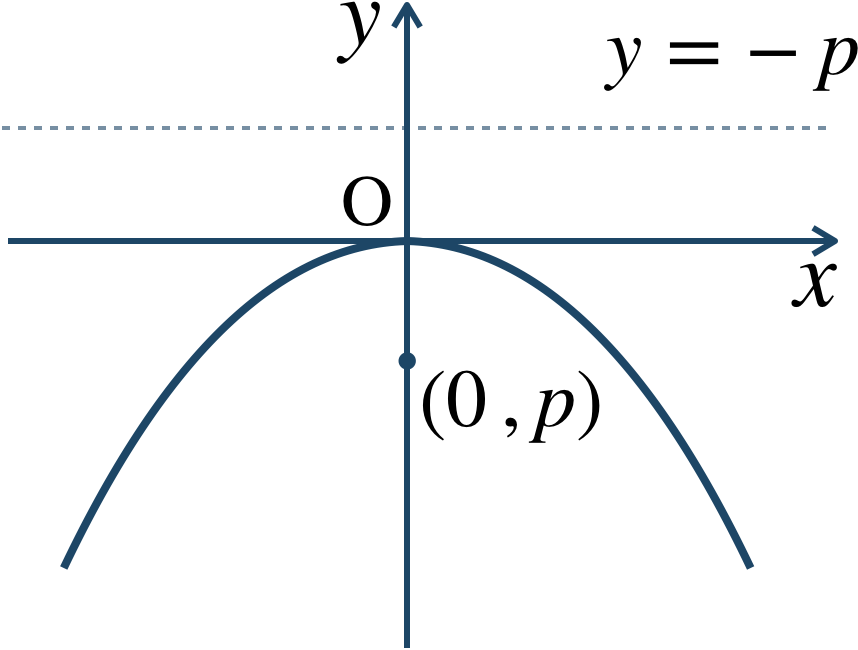
(ⅱ) \(p\lt0\) のとき
■ \(y\) 軸が軸の放物線
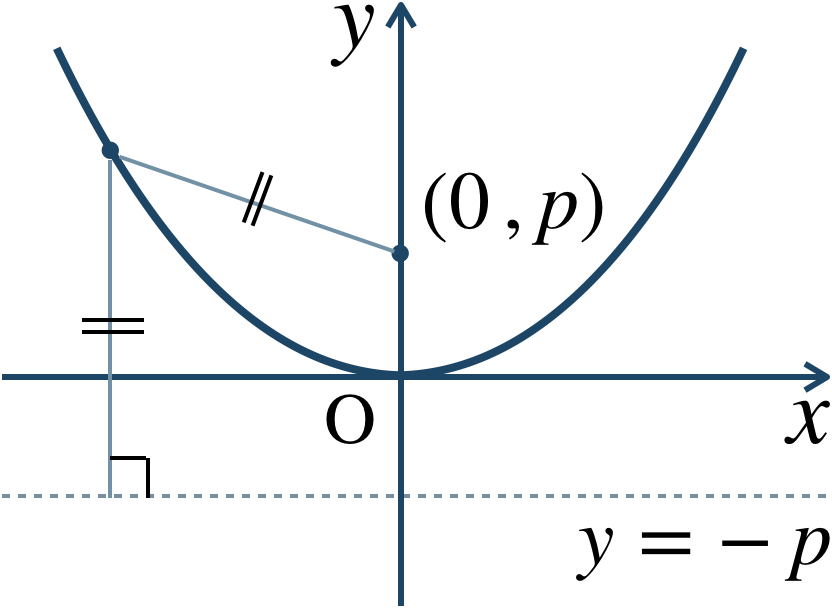
焦点 \((0~,~p)\) 、準線 \(y=-p\) の放物線は、
頂点は原点 \((0~,~0)\) である。
\(y\) 軸( \(x=0\) )が軸で、\(y\) 軸で対称となる。
概形は、
(ⅰ) \(p\gt0\) のとき、
(ⅱ) \(p\lt0\) のとき
問題解説:放物線の標準形
問題解説(1)
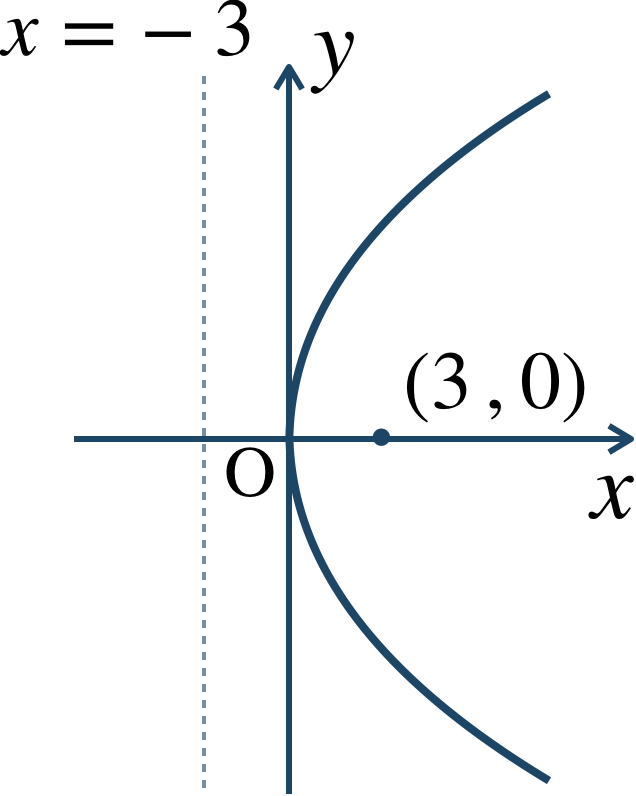
与えられた式を標準形に式変形すると、$$~~~y^2=4\cdot3\cdot x$$これより、\(x\) 軸が軸の放物線で \(p=3\) となるので、
焦点 \((3~,~0)\) 、準線 \(x=-3\)
また、概形は、
問題解説(2)
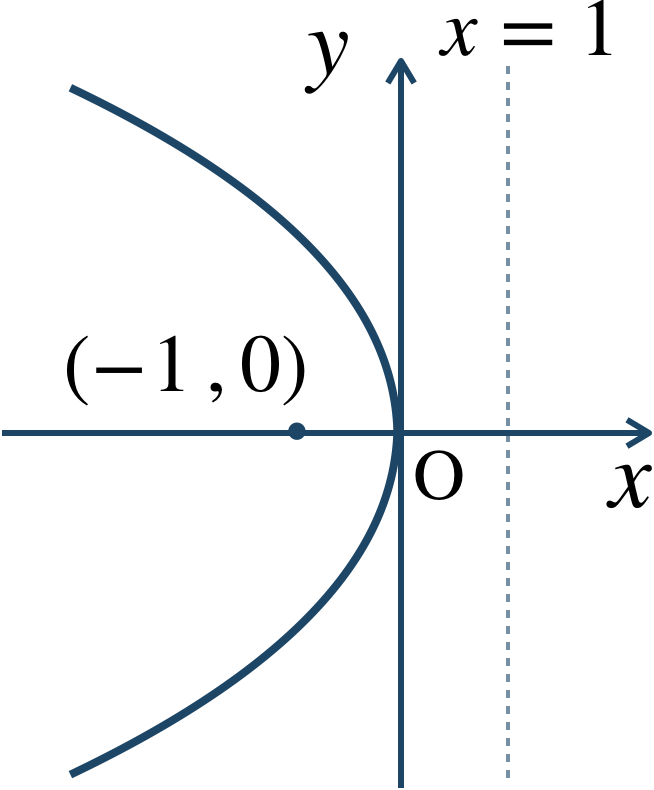
与えられた式を標準形に式変形すると、$$~~~y^2=4\cdot(-1)\cdot x$$これより、\(x\) 軸が軸の放物線で \(p=-1\) となるので、
焦点 \((-1~,~0)\) 、準線 \(x=1\)
また、概形は、
問題解説(3)
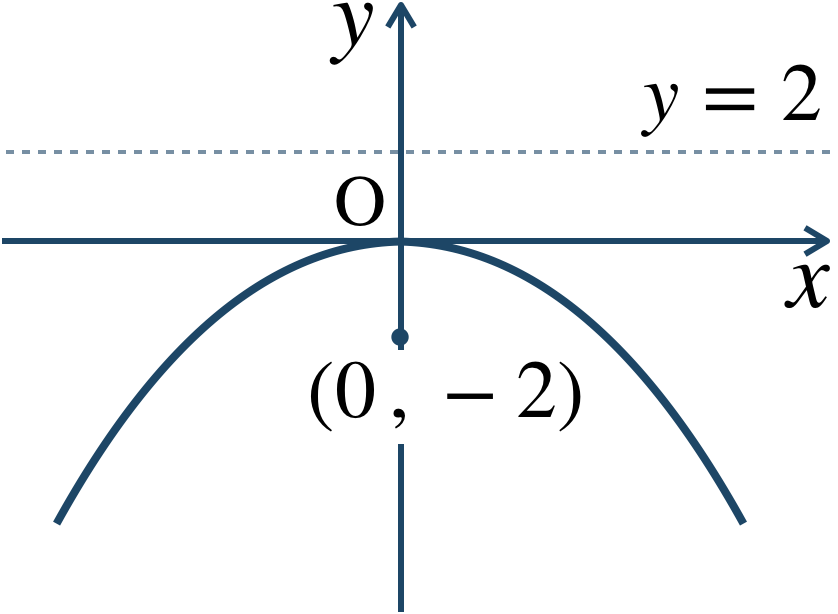
与えられた式を標準形に式変形すると、$$~~~x^2=4\cdot(-2)\cdot y$$これより、\(y\) 軸が軸の放物線で \(p=-2\) となるので、
焦点 \((0~,~-2)\) 、準線 \(y=2\)
また、概形は、
問題解説(4)
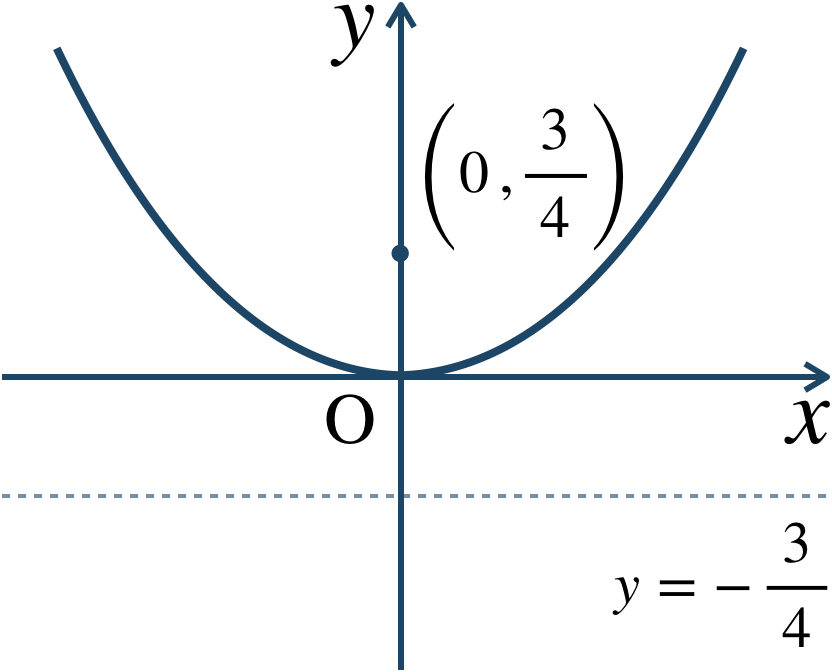
与えられた式を標準形に式変形すると、$$~~~x^2=4\cdot\frac{\, 3\,}{\,4 \,}\cdot y$$これより、\(y\) 軸が軸の放物線で \(p={\large \frac{\,3\,}{\,4\,}}\) となるので、
焦点 \((0~,~{\large \frac{\,3\,}{\,4\,}})\) 、準線 \(y=-{\large \frac{\,3\,}{\,4\,}}\)
また、概形は、
今回のまとめ
放物線の標準形について解説しました。標準形に式変形して、焦点と準線を読み取れるようになりましょう。