放物線の方程式の決定

2020.09.29

放物線の方程式の決定の解法
問題解説：放物線の方程式の決定
1. 問題解説(1)
2. 問題解説(2)
今回のまとめ

放物線の方程式の決定の解法

Point：放物線の方程式の決定与えられた条件が、
(1) 焦点 $(p~,~0)$ 、準線 $x=p$ のとき、
→ $x$ 軸が軸の放物線となり、

$$y^2=4px$$

この式に $p$ の値を代入して、放物線の方程式を求める。

(2) 焦点 $(0~,~p)$ 、準線 $y=p$ のとき、
→ $y$ 軸が軸の放物線となり、

$$x^2=4py$$

この式に $p$ の値を代入して、放物線の方程式を求める。

問題解説：放物線の方程式の決定

問題解説(1)

問題次の条件を満たす放物線の方程式を求めて、概形をかけ。
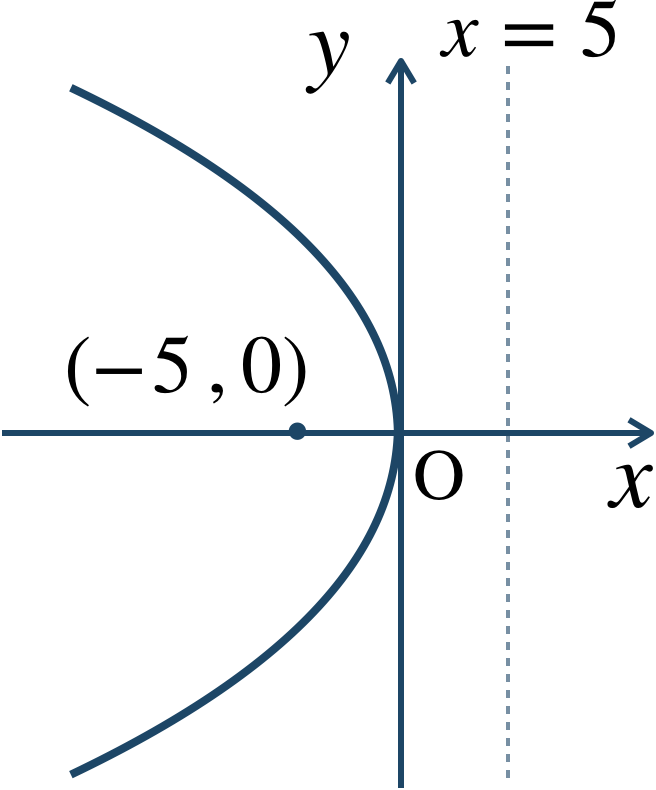
${\small (1)}~$焦点 $(-5~,~0)$ 、準線 $x=5$ の放物線。

焦点 $(-5~,~0)$ 、準線 $x=5$ であるので、この放物線は $x$ 軸が軸となる。
よって、放物線の方程式は、$$~~~y^2=4px$$となる。
$p=-5$ であるので、代入すると、$$~~~y^2=4\cdot(-5)\cdot x$$$$~~~y^2=-20x$$したがって、標準形は $y^2=-20x$ となり、概形は、

となる。

問題解説(2)

問題次の条件を満たす放物線の方程式を求めて、概形をかけ。
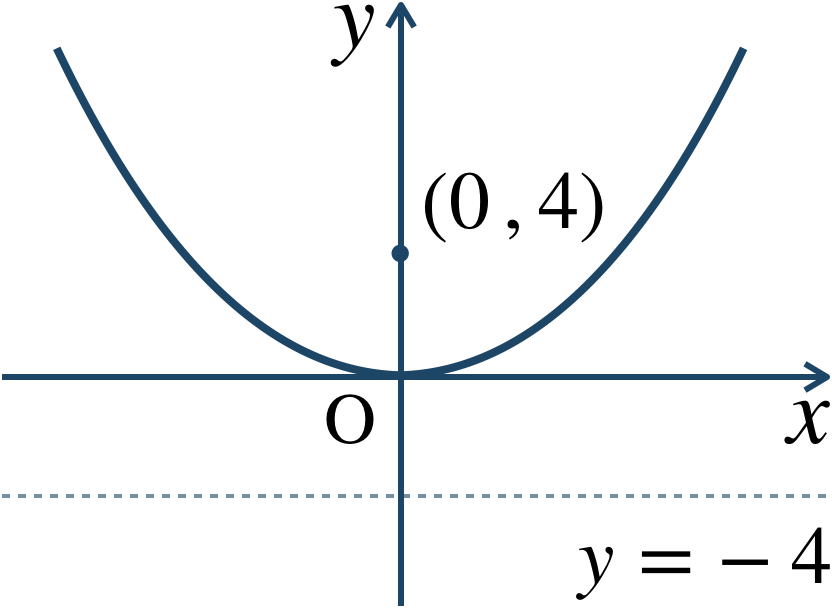
${\small (2)}~$焦点 $(0~,~4)$ 、頂点 $(0~,~0)$ の放物線。

焦点 $(0~,~4)$ で頂点 $(0~,~0)$ であるので、準線が $y=-4$ となる。
よって、この放物線は $x$ 軸が軸となり、放物線の方程式は、$$~~~x^2=4py$$となる。
$p=4$ であるので、代入すると、$$~~~x^2=4\cdot4\cdot y$$$$~~~x^2=16y$$したがって、標準形は $x^2=16y$ となり、概形は、

となる。