極座標と直交座標

2020.10.03

極座標と直交座標の解法
問題解説：極座標と直交座標
1. 問題解説(1)
2. 問題解説(2)
今回のまとめ

極座標と直交座標の解法

Point：極座標と直交座標極 ${\rm O}$、始線 ${\rm OX}$ に対して、極 ${\rm O}$ から点 ${\rm P}$ までの距離を $r$ 、動径 ${\rm OP}$ を表す角 $\theta$ を偏角とすると、

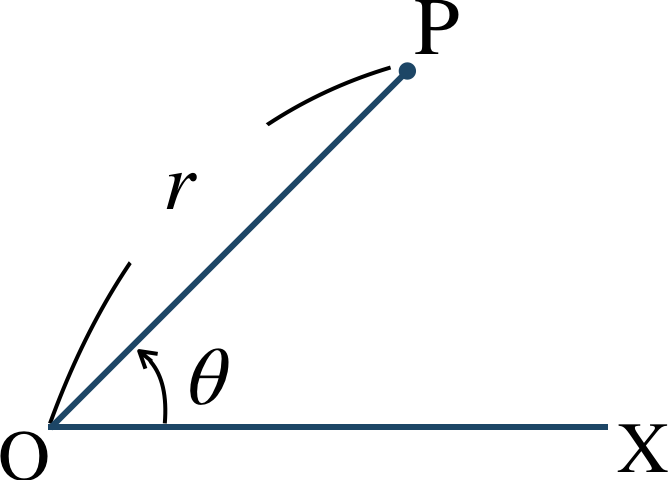
点 ${\rm P}$ の極座標を

$${\rm P}(r~,~\theta)$$

とする。

■ 極座標を直交座標で表す手順
① 極座標を座標平面上に表す。

② 図より、${\rm P}(x~,~y)$ は、$$~~~x=r\cos{\theta}~,~y=r\sin{\theta}$$を満たす。

■ 直交座標を極座標で表す手順
① 動径 ${\rm OP}$ の長さ $r$ を求める。$$~~~r=\sqrt{x^2+y^2}$$② 座標平面上に表し、偏角 $\theta$ を求める。

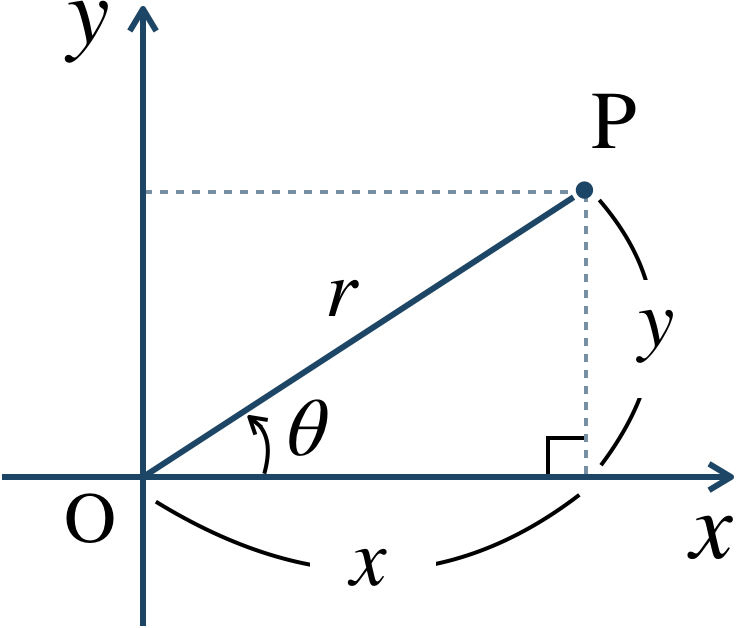
$$~~~\cos{\theta}=\frac{\,x \,}{\,r \,}~,~\sin{\theta}=\frac{\,y \,}{\,r \,}$$を満たす。

問題解説：極座標と直交座標

問題解説(1)

問題次の問いに答えよ。
${\small (1)}~$次の極座標を図示し、直交座標で表せ。$$~{\large ①}~{\rm A}\left(2~,~\frac{\,\pi \,}{\,3 \,}\right)~~~~~~\,{\large ②}~{\rm B}\left(4~,~-\frac{\,\pi \,}{\,4 \,}\right)$$$$~{\large ③}~{\rm C}\left(3~,~\frac{\,3 \,}{\,2 \,}\pi\right)~~~~{\large ④}~{\rm D}(1~,~\pi)$$

${\large ①}$ $r=2~,~\theta={\large \frac{\,\pi\,}{\,3\,}}$ より、座標平面上に表すと、

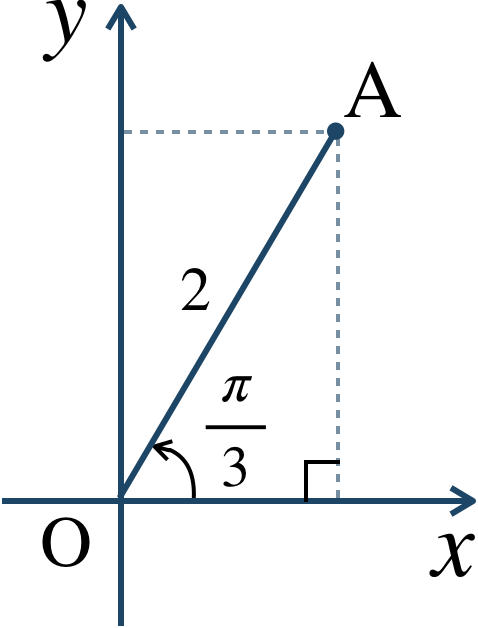
$$~~~x=2\cos{\frac{\,\pi \,}{\,3 \,}}=2\cdot\frac{\,1 \,}{\,2 \,}=1$$$$~~~y=2\sin{\frac{\,\pi \,}{\,3 \,}}=2\cdot\frac{\,\sqrt{3} \,}{\,2 \,}=\sqrt{3}$$したがって、直交座標で表すと、$$~~~\left(1~,~\sqrt{3}\right)$$となる。

${\large ②}$ $r=4~,~\theta=-{\large \frac{\,\pi\,}{\,4\,}}$ より、座標平面上に表すと、

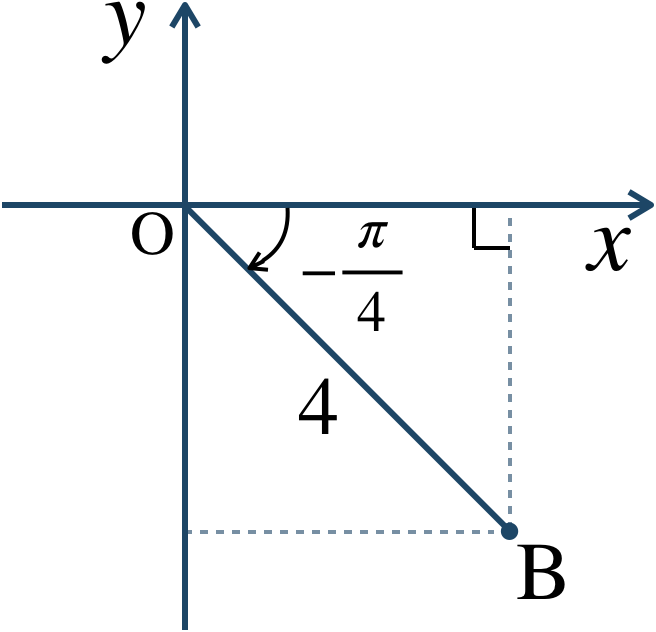
$$~~~x=4\cos\left(-{\frac{\,\pi \,}{\,4 \,}}\right)$$$$~~~~~=4\cdot\frac{\,\sqrt{2} \,}{\,2 \,}=2\sqrt{2}$$$$~~~y=4\sin\left(-{\frac{\,\pi \,}{\,4 \,}}\right)$$$$~~~~~=4\cdot\left(-\frac{\,\sqrt{2} \,}{\,2 \,}\right)=-2\sqrt{2}$$したがって、直交座標で表すと、$$~~~\left(2\sqrt{2}~,~-2\sqrt{2}\right)$$となる。

${\large ③}$ $r=3~,~\theta={\large \frac{\,3\,}{\,2\,}}\pi$ より、座標平面上に表すと、

$$~~~x=3\cos{\frac{\,3 \,}{\,2 \,}\pi}=3\cdot0=0$$$$~~~y=3\sin{\frac{\,3 \,}{\,2 \,}\pi}=3\cdot(-1)=-3$$したがって、直交座標で表すと、$$~~~(0~,~-3)$$となる。

${\large ④}$ $r=1~,~\theta=\pi$ より、座標平面上に表すと、

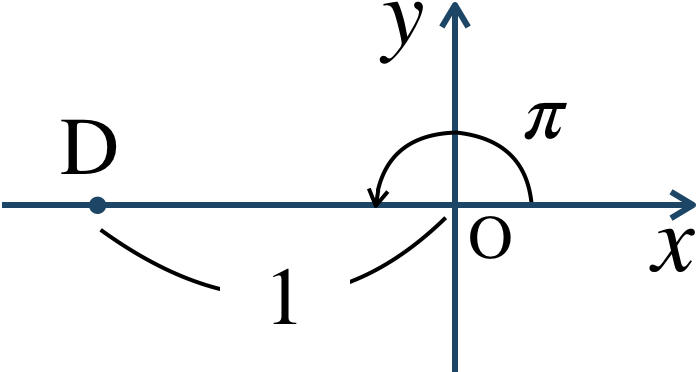
$$~~~x=1\cdot\cos{\pi}=1\cdot(-1)=-1$$$$~~~y=1\cdot\sin{\pi}=1\cdot0=0$$したがって、直交座標で表すと、$$~~~(-1~,~0)$$となる。

問題解説(2)

問題次の問いに答えよ。
${\small (2)}~$次の直交座標を極座標で表せ。$$~{\large ①}~{\rm E}(-1~,~1)~~~~~~{\large ②}~{\rm F}\left(3~,~\sqrt{3}\right)$$$$~{\large ③}~{\rm G}(0~,~4)~~~~~~~~{\large ④}~{\rm H}(2~,~0)$$

${\large ①}$ 動径 ${\rm OE}$ の長さを $r$ とすると、$$~~~r=\sqrt{(-1)^2+1^2}$$$$~~~~\,=\sqrt{1+1}=\sqrt{2}$$座標平面上に表すと、

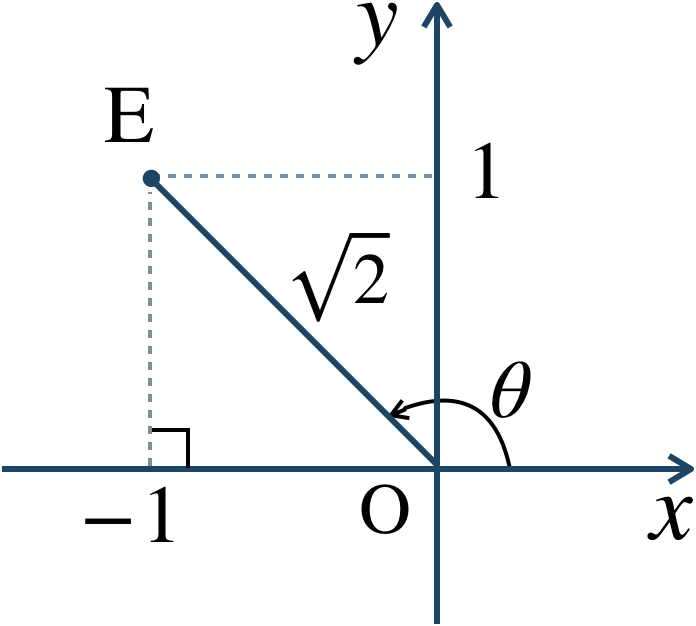
よって、偏角 $\theta$ は、$$~~~\theta=\frac{\,3 \,}{\,4 \,}\pi$$したがって、極座標で表すと、$$~~~\left(\sqrt{2}~,~\frac{\,3 \,}{\,4 \,}\pi\right)$$となる。

${\large ②}$ 動径 ${\rm OF}$ の長さを $r$ とすると、$$~~~r=\sqrt{3^2+\left(\sqrt{3}\right)^2}$$$$~~~~\,=\sqrt{9+3}$$$$~~~~\,=\sqrt{12}=2\sqrt{3}$$座標平面上に表すと、

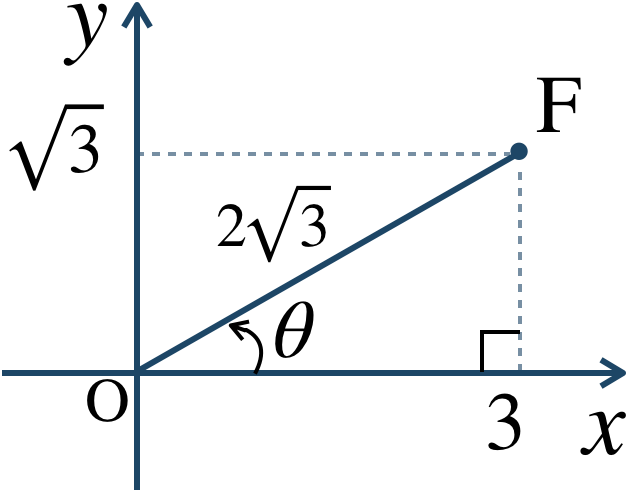
よって、偏角 $\theta$ は、$$~~~\theta=\frac{\,\pi \,}{\,6 \,}$$したがって、極座標で表すと、$$~~~\left(2\sqrt{3}~,~\frac{\,\pi \,}{\,6 \,}\right)$$となる。

${\large ③}$ 動径 ${\rm OG}$ の長さを $r$ とすると、$$~~~r=\sqrt{0^2+4^2}$$$$~~~~\,=\sqrt{4^2}=4$$座標平面上に表すと、

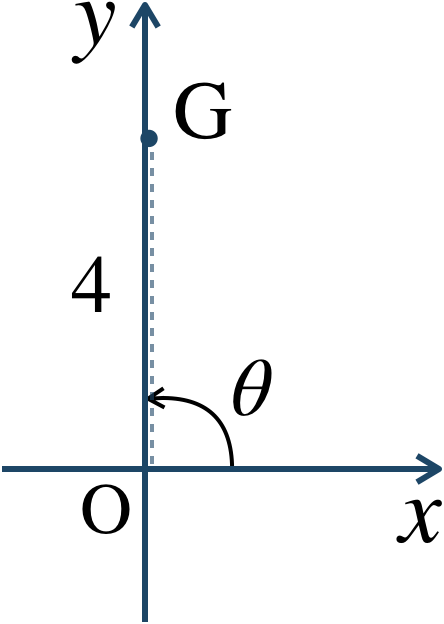
よって、偏角 $\theta$ は、$$~~~\theta=\frac{\,\pi \,}{\,2 \,}$$したがって、極座標で表すと、$$~~~\left(4~,~\frac{\,\pi \,}{\,2 \,}\right)$$となる。

${\large ④}$ 動径 ${\rm OH}$ の長さを $r$ とすると、$$~~~r=\sqrt{2^2+0^2}$$$$~~~~\,=\sqrt{2^2}=2$$座標平面上に表すと、

よって、偏角 $\theta$ は、$$~~~\theta=0$$したがって、極座標で表すと、$$~~~\left(2~,~0\right)$$となる。