複素数平面上の点の解法
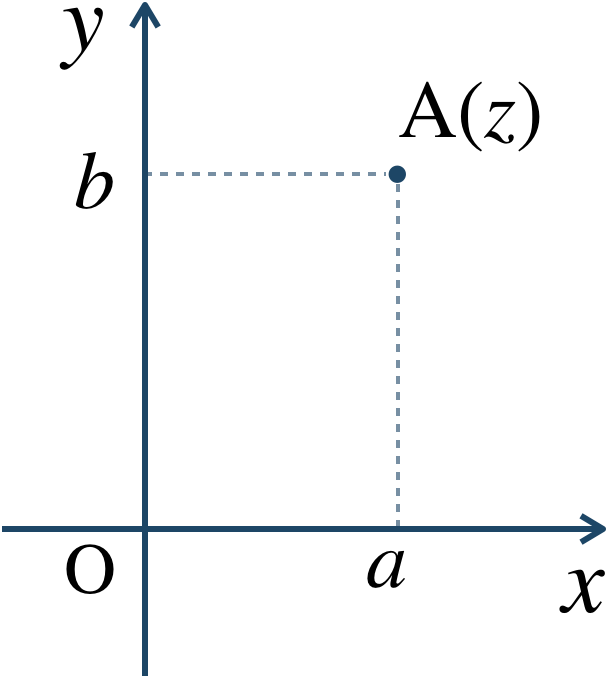
\(z=a+bi\) を表す点Aを
と表す。
問題解説:複素数平面上の点
問題解説(1)
\({\small (1)}~\)下の図において、点A〜Eはそれぞれどのような複素数を表すか答えよ。
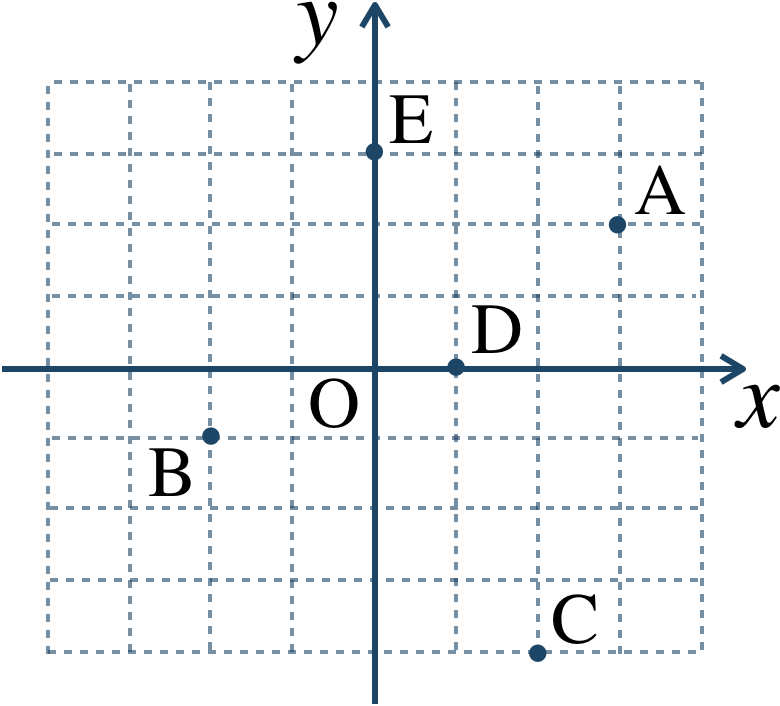
点Aの座標を読み取ると、$$~~~{\rm A}(3~,~2)$$\(x\) 座標が実部、\(y\) 座標が虚部となることより、
答えは \(3+2i\) となる。
点Bの座標を読み取ると、$$~~~{\rm B}(-2~,~-1)$$\(x\) 座標が実部、\(y\) 座標が虚部となることより、$$~~~(-2)+(-1)\cdot i=-2-i$$答えは \(-2-i\) となる。
点Cの座標を読み取ると、$$~~~{\rm C}(2~,~-4)$$\(x\) 座標が実部、\(y\) 座標が虚部となることより、$$~~~2+(-4)\cdot i=2-4i$$答えは \(2-4i\) となる。
点Dの座標を読み取ると、$$~~~{\rm D}(1~,~0)$$\(x\) 座標が実部、\(y\) 座標が虚部となることより、$$~~~1+0\cdot i=1$$答えは \(1\) となる。
点Eの座標を読み取ると、$$~~~{\rm E}(0~,~3)$$\(x\) 座標が実部、\(y\) 座標が虚部となることより、$$~~~0+3\cdot i=3i$$答えは \(3i\) となる。
問題解説(2)
\({\small (2)}~\)次の点を複素数平面上に表せ。$$~{\large ①}~{\rm F}(-3+i)~~~~{\large ②}~{\rm G}(4-i)$$$$~{\large ③}~{\rm H}(-1)~~~~~~~~~{\large ④}~{\rm I}(-3i)$$
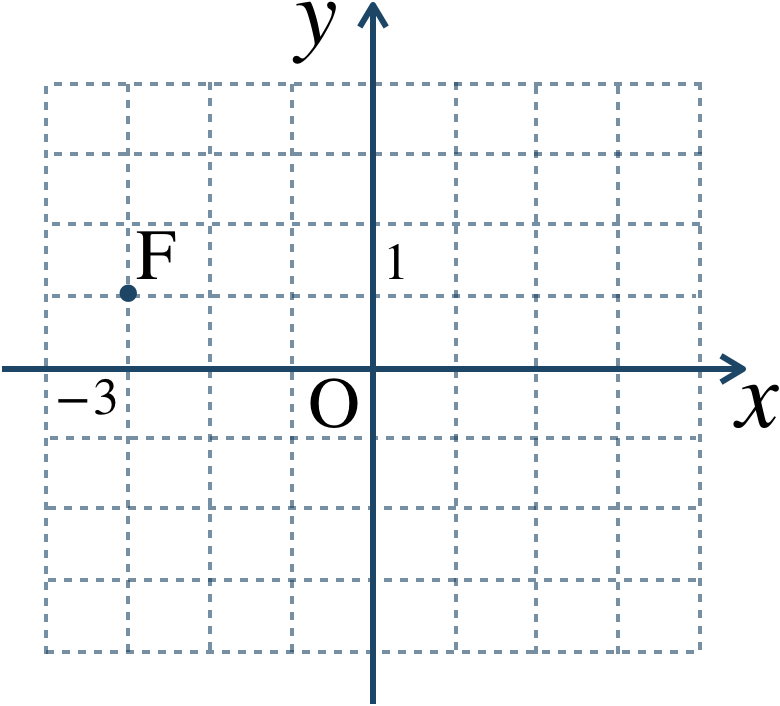
$$~{\large ①}~{\rm F}(-3+i) $$
実部 → \(x\) 座標より、\(-3\)
虚部 → \(y\) 座標より、\(1\)
よって、座標平面上で \((-3~,~1)\) となるので、
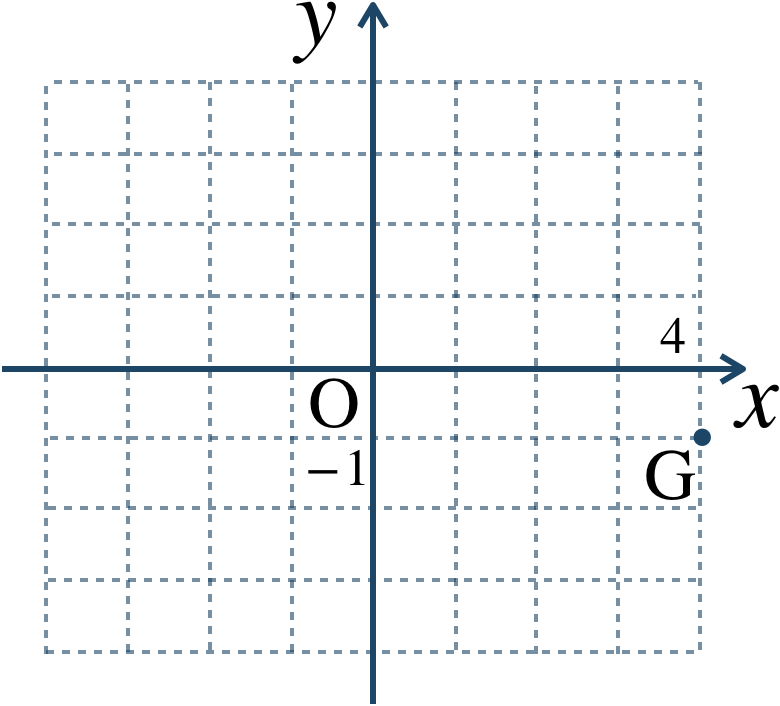
$$~{\large ②}~{\rm G}(4-i)$$
実部 → \(x\) 座標より、\(4\)
虚部 → \(y\) 座標より、\(-1\)
よって、座標平面上で \((4~,~-1)\) となるので、
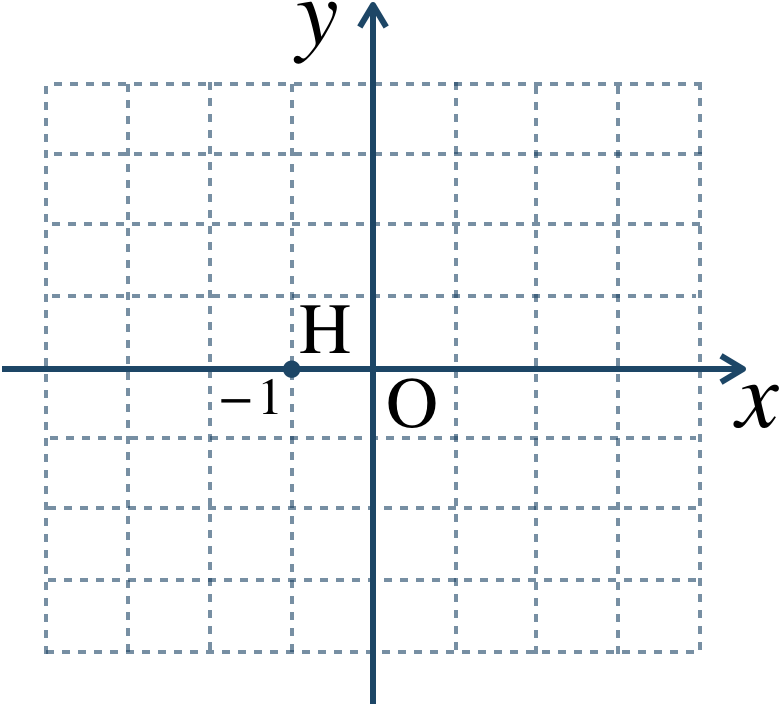
$$~{\large ③}~{\rm H}(-1)$$
実部 → \(x\) 座標より、\(-1\)
虚部 → \(y\) 座標より、\(0\)
よって、座標平面上で \((-1~,~0)\) となるので、
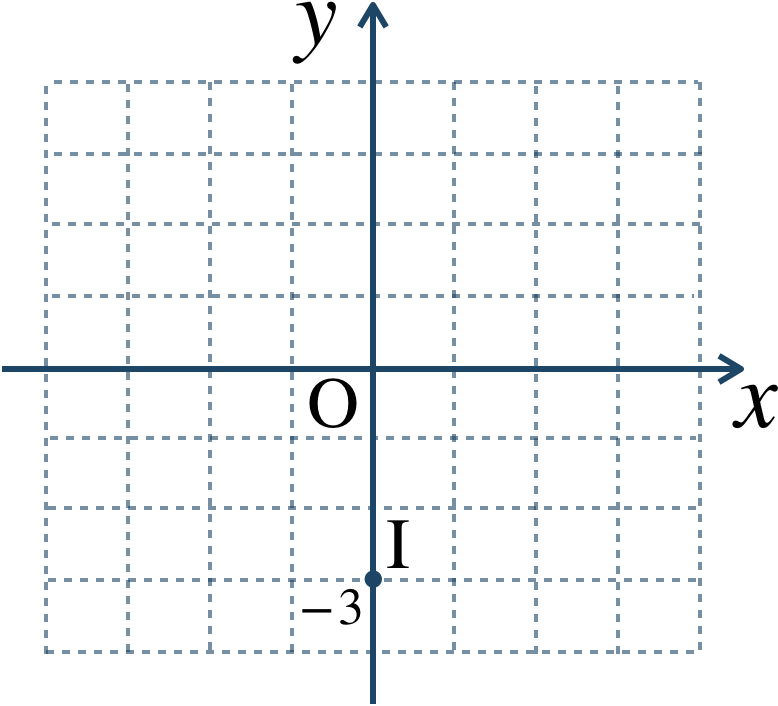
$$~{\large ④}~{\rm I}(-3i)$$
実部 → \(x\) 座標より、\(0\)
虚部 → \(y\) 座標より、\(-3\)
よって、座標平面上で \((0~,~-3)\) となるので、
今回のまとめ
複素数を座標平面上に表す方法を見てきました。実部 → \(x\) 座標、虚部 → \(y\) 座標を押さえておきましょう。