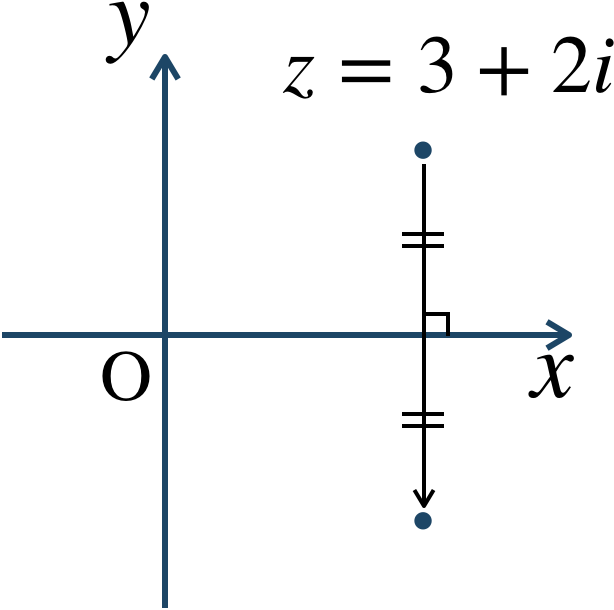
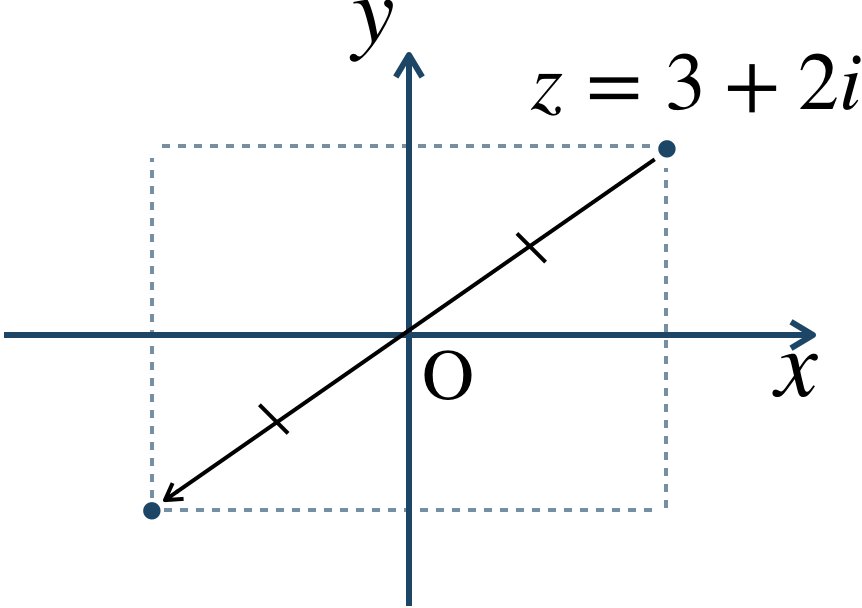
複素数平面上の対称移動の解法
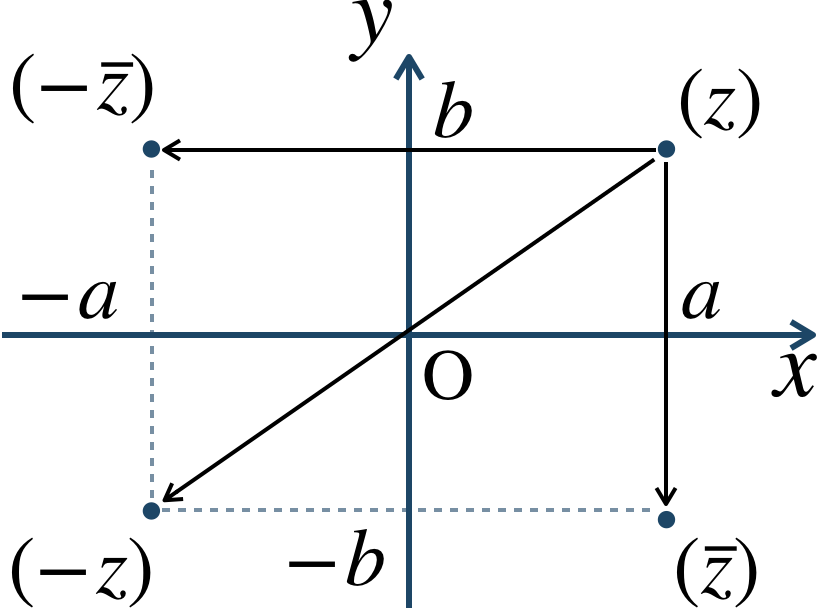
■ 実軸に関して対称な点
座標が \((a~,~-b)\) となり、複素数で表すと \(a-bi\)
また、\(z\) を用いて表すと、\(a+bi\) と共役な複素数であるので、
となる。
■ 原点に関して対称な点
座標が \((-a~,~-b)\) となり、複素数で表すと \(-a-bi\)
また、\(z\) を用いて表すと、\(a+bi\) と符号が逆の複素数であるので、
となる。
■ 虚軸に関して対称な点
座標が \((-a~,~b)\) となり、複素数で表すと \(-a+bi\)
また、\(z\) を用いて表すと、\(a+bi\) と共役な複素数の符号が逆であるので、
となる。
問題解説:複素数平面上の対称移動
問題解説(1)
\({\small (1)}~\)実軸に関して対称な点
\(z=3+2i\) より、座標は \((3~,~2)\) となる。
実軸= \(x\) 軸で対称な点の座標は、$$~~~(3~,~-2)$$よって、複素数で表すと \(3-2i\) となる。
また、\(z=3+2i\) より \(3-2i\) は共役な複素数となるので、$$~~~\overline {z}=3-2i$$したがって、答えは \(3-2i~,~\overline {z}\) となる。
問題解説(2)
\({\small (2)}~\)虚軸に関して対称な点
\(z=3+2i\) より、座標は \((3~,~2)\) となる。
虚軸= \(y\) 軸で対称な点の座標は、$$~~~(-3~,~2)$$よって、複素数で表すと \(-3+2i\) となる。
また、\(z=3+2i\) より \(-3+2i\) は共役な複素数かつ符号が逆となるので、$$~~~-\overline {z}=-3+2i$$したがって、答えは \(-3+2i~,~-\overline {z}\) となる。
問題解説(3)
\({\small (3)}~\)原点に関して対称な点
\(z=3+2i\) より、座標は \((3~,~2)\) となる。
原点で対称な点の座標は、$$~~~(-3~,~-2)$$よって、複素数で表すと \(-3-2i\) となる。
また、\(z=3+2i\) より \(-3-2i\) は符号が逆の複素数となるので、$$~~~-z=-3-2i$$したがって、答えは \(-3-2i~,~-z\) となる。
今回のまとめ
複素数平面上の点の対称移動は、座標平面上の位置関係と \(z\) の符号と共役な複素数 \(\overline {z}\) を考えて解きましょう。