複素数の絶対値の解法
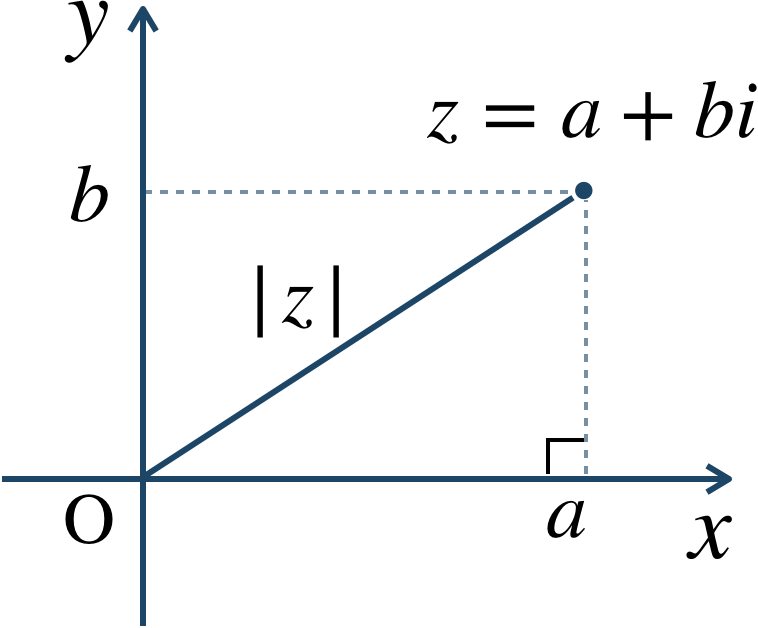
複素数 \(a+bi\) について、この複素数の絶対値は、
また、複素数平面上では、
\(|z|\) は原点からの距離を表す。
■ 複素数の絶対値の性質
複素数 \(z\) に対して、
問題解説:複素数の絶対値
問題解説(1)
\({\small (1)}~\)次の複素数の絶対値を求めよ。$$~{\large ①}~1+2i~~~~~~~~{\large ②}~3-4i$$$$~{\large ③}~-3i~~~~~~~~~~{\large ④}~5$$
\({\large ①}~z=1+2i\) とすると、$$~~~~~~|z|$$$$~=\sqrt{1^2+2^2}$$$$~=\sqrt{1+4}=\sqrt{5}$$したがって、答えは \(\sqrt{5}\) となる。
\({\large ②}~z=3-4i\) とすると、$$~~~~~~|z|$$$$~=\sqrt{3^2+(-4)^2}$$$$~=\sqrt{9+16}=\sqrt{25}=5$$したがって、答えは \(5\) となる。
\({\large ③}~z=0-3i\) とすると、$$~~~~~~|z|$$$$~=\sqrt{0^2+(-3)^2}$$$$~=\sqrt{0+9}=\sqrt{9}=3$$したがって、答えは \(3\) となる。
\({\large ④}~z=5+0\cdot i\) とすると、$$~~~~~~|z|$$$$~=\sqrt{5^2+0^2}$$$$~=\sqrt{25+0}=\sqrt{25}=5$$したがって、答えは \(5\) となる。
問題解説(2)
\({\small (2)}~\)複素数 \(z\) について、次のことを証明せよ。$$~{\large ①}~|z|=|-z|=|\overline {z}|$$$$~{\large ②}~|z|^2=z\overline {z}$$
\({\large ①}~\) [証明] \(z=a+bi\) とすると、
\(|z|\) は、$$~~~|z|=\sqrt{a^2+b^2}~~~\cdots~{\large ①}$$符号を逆にした複素数 \(-z=-a-bi\) より、\(|-z|\) は、$$~~~~~~|-z|$$$$~=\sqrt{(-a)^2+(-b)^2}$$$$~=\sqrt{a^2+b^2}~~~\cdots~{\large ②}$$次に、共役な複素数 \(\overline {z}=a-bi\) より、\(\overline {z}\) は、$$~~~~~~|\overline {z}|$$$$~=\sqrt{a^2+(-b)^2}$$$$~=\sqrt{a^2+b^2}~~~\cdots~{\large ③}$$したがって、①と②と③より、$$~~~|z|=|-z|=|\overline {z}|$$[終]
\({\large ②}~\) [証明] \(z=a+bi\) とすると、
絶対値 \(|z|\) は、$$~~~|z|=\sqrt{a^2+b^2}$$よって、\(|z|^2\) は、$$~~~|z|^2=a^2+b^2~~~\cdots~{\large ①}$$また、共役な複素数 \(\overline {z}=a-bi\) より、$$~~~~~~z|z|$$$$~=(a+bi)(a-bi)$$$$~=a^2-b^2i^2$$ここで、\(i^2=-1\) より、$$~=a^2-b^2\cdot (-1)$$$$~=a^2+b^2~~~\cdots~{\large ②}$$したがって、①と②より、$$~~~|z|^2=z\overline {z}$$[終]
今回のまとめ
複素数の絶対値の求め方は、座標平面上の原点からの距離として覚えていきましょう。また、複素数の性質 \(|z|^2=z\overline {z}\) は大事な式であるので覚えていきましょう。