複素数平面上の2点間の距離の解法
Point:複素数平面上の2点間の距離複素数 \(\alpha~,~\beta\) があり、複素数平面上の2点 \({\rm A}(\alpha)~,~{\rm B}(\beta)\) について、

この2点間の距離 \({\rm AB}\) は、
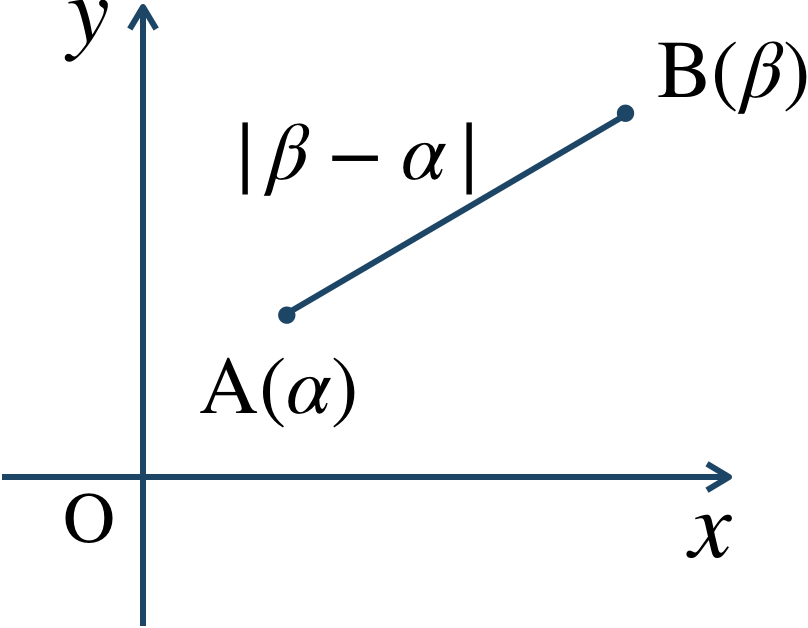
この2点間の距離 \({\rm AB}\) は、
$${\rm AB}=|\beta-\alpha|$$
となる。
解法の手順は、
① 複素数 \(\beta-\alpha\) を求める。
② 絶対値の公式より、\(|\beta-\alpha|\) を求める。
問題解説:複素数平面上の2点間の距離
問題解説(1)
問題次の2点間の距離を求めよ。$${\small (1)}~\alpha=-1+2i~,~\beta=3+5i$$
\(\alpha=-1+2i~,~\beta=3+5i\) より、$$~~~~~~\beta-\alpha$$$$~=(3+5i)-(-1+2i)$$$$~=3+5i+1-2i$$$$~=4+3i$$よって、$$~~~~~~|\beta-\alpha|$$$$~=\sqrt{4^2+3^2}$$$$~=\sqrt{16+9}$$$$~=\sqrt{25}=5$$したがって、2点間の距離は \(5\) となる。
問題解説(2)
問題次の2点間の距離を求めよ。$${\small (2)}~\alpha=-5-6i~,~\beta=1-2i$$
\(\alpha=-5-6i~,~\beta=1-2i\) より、$$~~~~~~\beta-\alpha$$$$~=(1-2i)-(-5-6i)$$$$~=1-2i+5+6i$$$$~=6+4i$$よって、$$~~~~~~|\beta-\alpha|$$$$~=\sqrt{6^2+4^2}$$$$~=\sqrt{36+16}$$$$~=\sqrt{52}=2\sqrt{13}$$したがって、2点間の距離は \(2\sqrt{13}\) となる。
今回のまとめ
複素数平面上の2点間の距離を求めるときは、まずは2点の差の複素数 \(\beta-\alpha\) を求めましょう。

【問題一覧】数学Ⅲ|複素数平面
このページは「高校数学Ⅲ:複素数平面」の問題一覧ページとなります。解説の見たい単元名がわからないとき...


