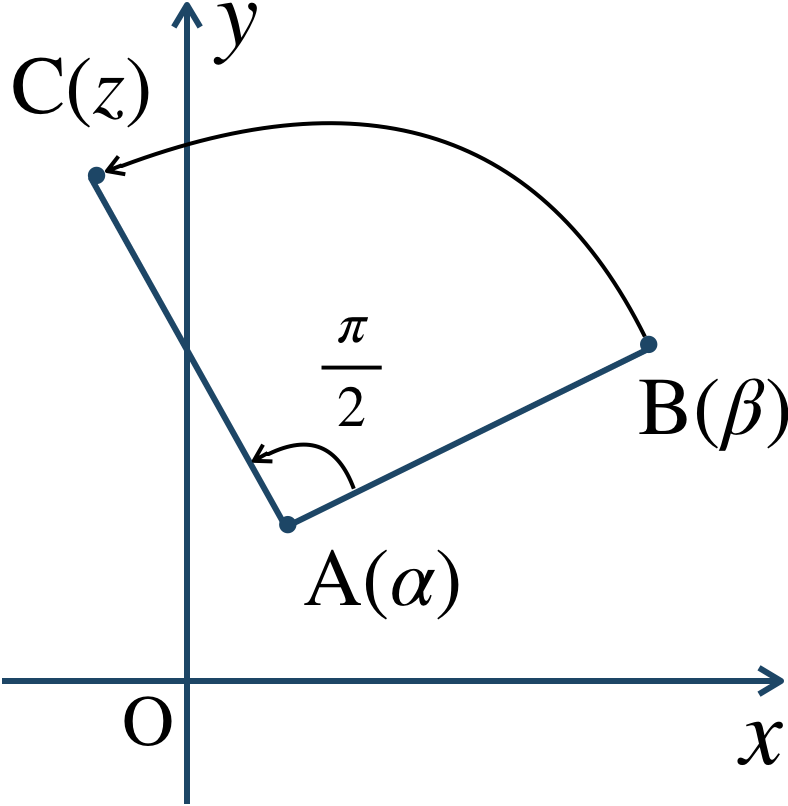
点を中心とする回転

2020.09.102020.09.13

点を中心とする回転の解法
問題解説：点を中心とする回転
1. 問題解説(1)
2. 問題解説(2)
今回のまとめ

点を中心とする回転の解法

Point：点を中心とする回転点 ${\rm A}(\alpha)$ を中心として、点 ${\rm B}(\beta)$ を $\theta$ 回転させた点 ${\rm C}(z)$ は、

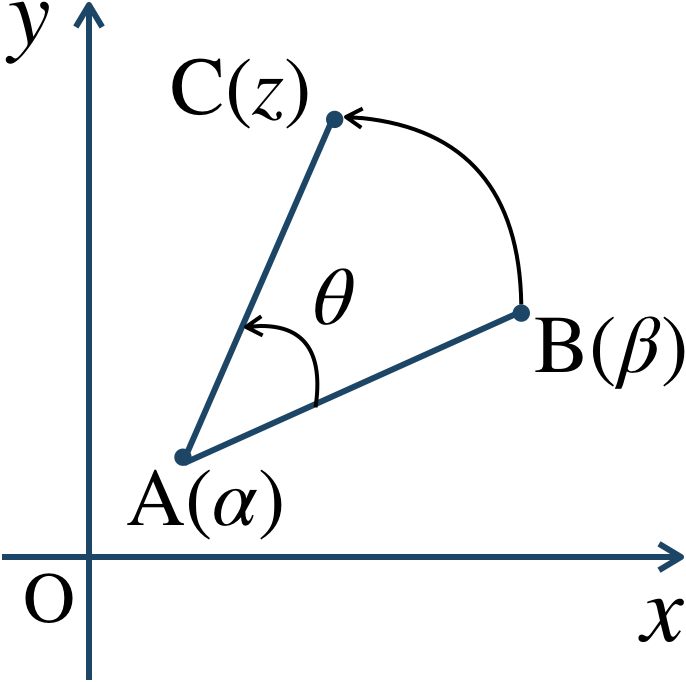
これを点 ${\rm A}(\alpha)$ が原点にくるように平行移動させると、点 ${\rm B}(\beta)$ と点 ${\rm C}(z)$ はそれぞれ $\beta-\alpha$ と $z-\alpha$ に平行移動される。

よって、点 ${\rm C’}(z-\alpha)$ は、点 ${\rm B’}(\beta-\alpha)$ を $\theta$ 回転した点となるので、$$~~~z-\alpha=(\cos{\theta}+i\sin{\theta})(\beta-\alpha)$$よって、$z$ は、

$$z=(\cos{\theta}+i\sin{\theta})(\beta-\alpha)+\alpha$$

問題解説：点を中心とする回転

問題解説(1)

問題複素数平面上の点について、次の問いに答えよ。
${\small (1)}~$点 ${\rm A}(1+i)$ を中心として、点 ${\rm B}(3+2i)$ を ${\large \frac{\,\pi\,}{\,6\,}}$ 回転させた点 ${\rm C}$ を複素数で表せ。

$\alpha=1+i~,~\beta=3+2i$ とし、点 ${\rm C}$ の表す複素数を $z$ とする。

これを、点 ${\rm A}(\alpha)$ が原点にくるように平行移動させると、$\beta$ と $z$ はそれぞれ、$$~~~\beta-\alpha~,~z-\alpha$$となる。
よって、$z-\alpha$ は $\beta-\alpha$ を ${\large \frac{\,\pi\,}{\,6\,}}$ 回転した点となるので、$$~~~z-\alpha=\left(\cos{\frac{\,\pi \,}{\,6 \,}}+i\sin{\frac{\,\pi \,}{\,6 \,}}\right)(\beta-\alpha)$$$\alpha$ を移項して、$$~~~z=\left(\cos{\frac{\,\pi \,}{\,6 \,}}+i\sin{\frac{\,\pi \,}{\,6 \,}}\right)(\beta-\alpha)+\alpha$$ここで、$$~~~~~~\beta-\alpha$$$$~=(3+2i)-(1+i)=2+i$$また、$\sin{}~,~\cos{}$ を計算すると、単位円より、

これらより、$z$ は、$$~~~~~~z$$$$~=\left(\frac{\,\sqrt{3} \,}{\,2 \,}+\frac{\,1 \,}{\,2 \,}i\right)(2+i)+(1+i)$$$$~=\sqrt{3}+\frac{\,\sqrt{3} \,}{\, 2\,}i+i+\frac{\,1 \,}{\,2 \,}i^2+1+i$$$i^2=-1$ より、$$~=\sqrt{3}-\frac{\,1 \,}{\, 2\,}+1+\frac{\,\sqrt{3} \,}{\,2 \,}i+i+i$$$$~=\frac{\,2\sqrt{3}+1 \,}{\,2 \,}+\frac{\, \sqrt{3}+4\,}{\,2 \,}i$$したがって、点 ${\rm C}$ を表す複素数は、$$~~~\frac{\,2\sqrt{3}+1 \,}{\,2 \,}+\frac{\, \sqrt{3}+4\,}{\,2 \,}i$$となる。

問題解説(2)

問題複素数平面上の点について、次の問いに答えよ。
${\small (2)}~$点 ${\rm A}(1+2i)$ を中心として、点 ${\rm B}(5+4i)$ を ${\large \frac{\,\pi\,}{\,2\,}}$ 回転させた点 ${\rm C}$ を複素数で表せ。

$\alpha=1+2i~,~\beta=5+4i$ とし、点 ${\rm C}$ の表す複素数を $z$ とする。

これを、点 ${\rm A}(\alpha)$ が原点にくるように平行移動させると、$\beta$ と $z$ はそれぞれ、$$~~~\beta-\alpha~,~z-\alpha$$となる。
よって、$z-\alpha$ は $\beta-\alpha$ を ${\large \frac{\,\pi\,}{\,2\,}}$ 回転した点となるので、$$~~~z-\alpha=\left(\cos{\frac{\,\pi \,}{\,2 \,}}+i\sin{\frac{\,\pi \,}{\,2\,}}\right)(\beta-\alpha)$$$\alpha$ を移項して、$$~~~z=\left(\cos{\frac{\,\pi \,}{\,2 \,}}+i\sin{\frac{\,\pi \,}{\,2\,}}\right)(\beta-\alpha)+\alpha$$ここで、$$~~~~~~\beta-\alpha$$$$~=(5+4i)-(1+2i)=4+2i$$また、$\sin{}~,~\cos{}$ を計算すると、単位円より、

これらより、$z$ は、$$~~~~~~z$$$$~=(0+i\cdot 1)(4+2i)+(1+2i)$$$$~=i(4+2i)+(1+2i)$$$$~=4i+2i^2+1+2i$$$i^2=-1$ より、$$~=4i-2+1+2i$$$$~=-1+6i$$したがって、点 ${\rm C}$ を表す複素数は、$-1+6i$ となる。