ド・モアブルの定理の解法
絶対値 \(r\) は \(n\) 乗して \(r^n\) に、
偏角 \(\theta\) は \(n\) 倍して \(n\theta\) になる。
問題解説:ド・モアブルの定理
問題解説(1)
\(z={\large \frac{\,1\,}{\,2\,}}+{\large \frac{\,\sqrt{3}\,}{\,2\,}}i\) とすると、絶対値は、$$~~~~~~|z|$$$$~=\sqrt{\left(\frac{\,1 \,}{\,2 \,}\right)^2+\left(\frac{\,\sqrt{3} \,}{\,2 \,}\right)^2}$$$$~=\sqrt{\frac{\,1 \,}{\,4 \,}+\frac{\,3 \,}{\,4 \,}}=\sqrt{\frac{\,4 \,}{\,4 \,}}=1$$また、\(z\) を複素数平面上に表すと、
図より、偏角は \(\theta={\large \frac{\,\pi\,}{\,3\,}}\) となる。
よって、\(z\) を極形式で表すと、$$~~~z=\cos{\frac{\,\pi \,}{\,3 \,}}+i\sin{\frac{\,\pi \,}{\,3 \,}}$$これより、\(\left({\large \frac{\,1\,}{\,2\,}}+{\large \frac{\,\sqrt{3}\,}{\,2\,}}i\right)^6\) は、ド・モアブルの定理より、$$~~~~~~z^6$$$$~=\cos{\left(6\times\frac{\,\pi \,}{\,3 \,}\right)}+i\sin{\left(6\times\frac{\,\pi \,}{\,3 \,}\right)}$$$$~=\cos{2\pi}+i\sin{2\pi}$$\(\sin{}~,~\cos{}\) を計算すると、単位円より、
$$~=1+i\times0=1$$したがって、答えは \(1\) となる。
問題解説(2)
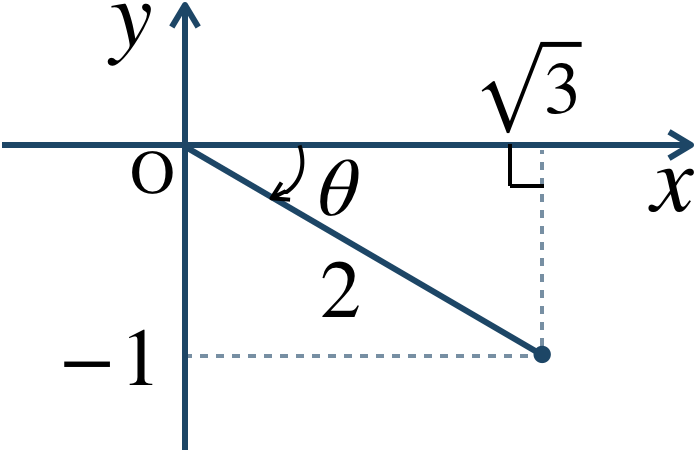
\(z=\sqrt{3}-i\) とすると、絶対値は、$$~~~~~~|z|$$$$~=\sqrt{(\sqrt{3})^2+(-1)^2}$$$$~=\sqrt{3+1}=\sqrt{4}=2$$また、\(z\) を複素数平面上に表すと、
図より、偏角は \(\theta=-{\large \frac{\,\pi\,}{\,6\,}}\) となる。
よって、\(z\) を極形式で表すと、$$~~~z=2\left\{ \cos\left(-{\frac{\,\pi \,}{\,6 \,}}\right)+i\sin\left(-{\frac{\,\pi \,}{\,3 \,}}\right)\right\}$$これより、\(\left(\sqrt{3}-i\right)^9\) は、ド・モアブルの定理より、$$~~~~~~z^9$$$$~={\small 2^9\left\{ \cos\left(-{\frac{\,\pi \,}{\,6 \,}}\times 9\right)+i\sin\left(-{\frac{\,\pi \,}{\,3 \,}}\times 9\right)\right\}}$$$$~=2^9\left\{ \cos\left(-{\frac{\,3 \,}{\,2 \,}}\pi\right)+i\sin\left(-{\frac{\,3\,}{\,2\,}}\pi\right)\right\}$$\(\sin{}~,~\cos{}\) を計算すると、単位円より、
また、\(2^9=512\) より、$$~=512(0+i\times 1)=512i$$したがって、答えは \(512i\) となる。
問題解説(3)
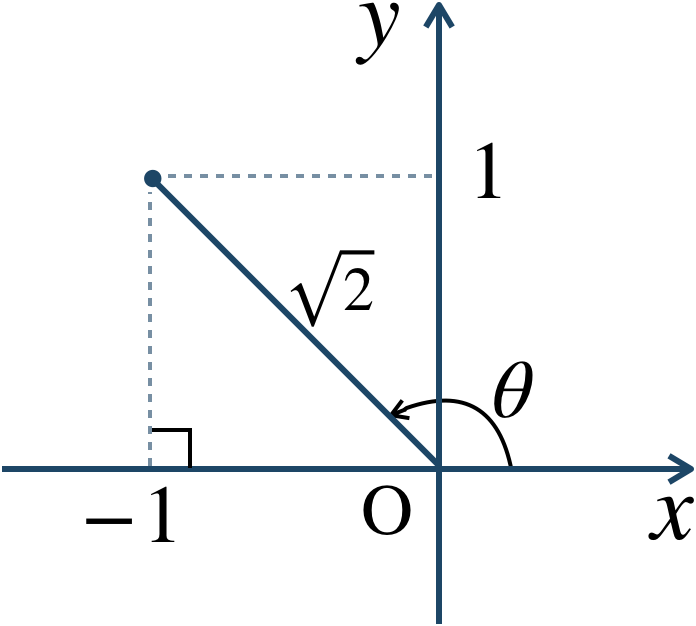
\(z=-1+i\) とすると、絶対値は、$$~~~~~~|z|$$$$~=\sqrt{(-1)^2+1^2}$$$$~=\sqrt{1+1}=\sqrt{2}$$また、\(z\) を複素数平面上に表すと、
図より、偏角は \(\theta={\large \frac{\,3\,}{\,4\,}}\pi\) となる。
よって、\(z\) を極形式で表すと、$$~~~z=\sqrt{2}\left(\cos{\frac{\,3 \,}{\,4 \,}\pi}+i\sin{\frac{\,3 \,}{\, 4\,}\pi}\right)$$これより、\((-1+i)^{-4}\) は、ド・モアブルの定理より、$$~~~~~~z^{-4}$$$$~={\scriptsize \left(\sqrt{2}\right)^{-4}\left\{\cos\left({-4\times \frac{\,3 \,}{\,4 \,}\pi}\right)+i\sin\left({-4\times \frac{\,3 \,}{\,4 \,}\pi}\right)\right\}}$$$$~=\left(\sqrt{2}\right)^{-4}\{\cos{\left(-3\pi\right)}+i\sin{\left(-3\pi\right)}\}$$\(\sin{}~,~\cos{}\) を計算すると、単位円より、
また、$$~~~\left(\sqrt{2}\right)^{-4}=\frac{\,1 \,}{\,\left(\sqrt{2}\right)^4 \,}=\frac{\,1 \,}{\, 4\,}$$よって、$$~~~z^{-4}=\frac{\,1 \,}{\,4 \,}(-1+i\times 0)=-\frac{\,1 \,}{\,4 \,}$$したがって、答えは \(-{\Large \frac{\,1\,}{\,4\,}}\) となる。
今回のまとめ
ド・モアブルの定理との使い方について解説しました。絶対値と偏角のそれぞれの計算方法をしっかりと覚えていきましょう。