１のn乗根

１のn乗根の解法
問題解説：１のn乗根
1. 問題解説(1)
2. 問題解説(2)
今回のまとめ

１のn乗根の解法

Point：１のn乗根方程式 $z^n=1$ の解は、
① 解 $z$ を、$$~~~z=r(\cos{\theta}+i\sin{\theta})$$とおく。ただし、$r\gt0$
② $z^n$ をド・モアブルの定理より求める。$$~~~z^n=r^n(\cos{n\theta}+i\sin{n\theta})$$③ 右辺の $1$ を極形式で表す。

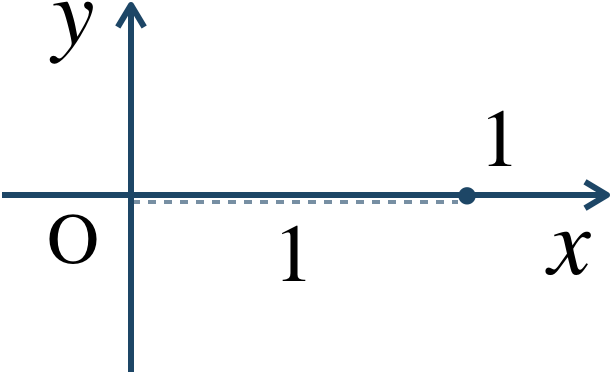
絶対値 $1$ 、偏角 $0$ より、$$~~~1=\cos{0}+i\sin{0}$$④ $z^n=1$ より、②と③の式を比較すると、
絶対値は $r^n=1$
　$r\gt0$ より、$r=1$
偏角は、三角関数の周期性を考えて、$k$ を整数として、$$~~~n\theta=0+2\pi\times k$$⑤ $0≦\theta\lt2\pi$ の範囲に含まれるように $k$ の値を考え $\theta$ を求める。
⑥ $r$ と $\theta$ を①に代入して、$z$ を求める。

問題解説：１のn乗根

問題解説(1)

問題次の問いに答えよ。
${\small (1)}~$１の $4$ 乗根を方程式 $z^4=1$ より求めよ。

$z^4=1$ の解 $z$ を、$$~~~z=r(\cos{\theta}+i\sin{\theta})~~~\cdots~{\large ①}$$とおく。ただし、$r\gt0$
$z^4$ はド・モアブルの定理より、$$~~~z^4=r^4(\cos{4\theta}+i\sin{4\theta})~~~\cdots~{\large ②}$$
また、右辺の $1$ を極形式で表すと、$$~~~1=\cos{0}+i\sin{0}~~~\cdots~{\large ③}$$$z^4=1$ より、②と③を比較すると、
絶対値は、$r^4=1$
$r\gt0$ であるので、$r=1$

また、偏角は $k$ を整数として、$$~~~4\theta=0+2\pi \times k$$$$~~~4\theta=2k\pi$$両辺を $4$ で割ると、$$~~~\theta=\frac{\,k \,}{\,2 \,}\pi$$$0≦\theta\lt2\pi$ の範囲で考えると、

$k=0$ のとき、$\theta=0$
$k=1$ のとき、$\theta={\large \frac{\,\pi\,}{\,2\,}}$
$k=2$ のとき、$\theta=\pi$
$k=3$ のとき、$\theta={\large \frac{\,3\,}{\,2\,}}\pi$

よって、それぞれの場合で①に代入し $z$ を求めると、
$k=0$ のとき、$$~~~z=1\cdot\left(\cos{0}+i\sin{0}\right)$$$$~~~~~=1+i\times 0=1$$$k=1$ のとき、$$~~~z=1\cdot\left(\cos{\frac{\,\pi \,}{\,2 \,}}+i\sin{\frac{\,\pi \,}{\,2 \,}}\right)$$$$~~~~~=0+i\times 1=i$$$k=2$ のとき、$$~~~z=1\cdot\left(\cos{\pi}+i\sin{\pi}\right)$$$$~~~~~=-1+i\times 0=-1$$$k=3$ のとき、$$~~~z=1\cdot\left(\cos{\frac{\,3\,}{\,2 \,}\pi}+i\sin{\frac{\,3 \,}{\,2 \,}\pi}\right)$$$$~~~~~=0+i\times (-1)=-i$$

したがって、答えは$$~~~z=1~,~-1~,~i~,~-i$$まとめると、$$~~~z=\pm1~,~\pm i$$となる。

問題解説(2)

問題次の問いに答えよ。
${\small (2)}~$１の $6$ 乗根を方程式 $z^6=1$ より求めよ。

$z^6=1$ の解 $z$ を、$$~~~z=r(\cos{\theta}+i\sin{\theta})~~~\cdots~{\large ①}$$とおく。ただし、$r\gt0$
$z^6$ はド・モアブルの定理より、$$~~~z^6=r^6(\cos{6\theta}+i\sin{6\theta})~~~\cdots~{\large ②}$$
また、右辺の $1$ を極形式で表すと、$$~~~1=\cos{0}+i\sin{0}~~~\cdots~{\large ③}$$$z^4=1$ より、②と③を比較すると、
絶対値は、$r^6=1$
$r\gt0$ であるので、$r=1$

また、偏角は $k$ を整数として、$$~~~6\theta=0+2\pi \times k$$$$~~~6\theta=2k\pi$$両辺を $6$ で割ると、$$~~~\theta=\frac{\,k \,}{\,3 \,}\pi$$$0≦\theta\lt2\pi$ の範囲で考えると、

$k=0$ のとき、$\theta=0$
$k=1$ のとき、$\theta={\large \frac{\,\pi\,}{\,3\,}}$
$k=2$ のとき、$\theta={\large \frac{\,2\,}{\,3\,}}\pi$
$k=3$ のとき、$\theta=\pi$
$k=4$ のとき、$\theta={\large \frac{\,4\,}{\,3\,}}\pi$
$k=5$ のとき、$\theta={\large \frac{\,5\,}{\,3\,}}\pi$

よって、それぞれの場合で①に代入し $z$ を求めると、
$k=0$ のとき、$$~~~z=1\cdot\left(\cos{0}+i\sin{0}\right)$$$$~~~~~=1+i\times 0=1$$$k=1$ のとき、$$~~~z=1\cdot\left(\cos{\frac{\,\pi \,}{\,3 \,}}+i\sin{\frac{\,\pi \,}{\,3 \,}}\right)$$$$~~~~~=\frac{\,1 \,}{\,2 \,}+\frac{\,\sqrt{3} \,}{\,2 \,}i$$$k=2$ のとき、$$~~~z=1\cdot\left(\cos{\frac{\,2 \,}{\,3 \,}\pi}+i\sin{\frac{\,2 \,}{\,3 \,}\pi}\right)$$$$~~~~~=-\frac{\,1 \,}{\,2 \,}+\frac{\,\sqrt{3} \,}{\,2 \,}i$$$k=3$ のとき、$$~~~z=1\cdot\left(\cos{\pi}+i\sin{\pi}\right)$$$$~~~~~=-1+i\times 0=-1$$$k=4$ のとき、$$~~~z=1\cdot\left(\cos{\frac{\,4 \,}{\,3 \,}\pi}+i\sin{\frac{\,4 \,}{\,3 \,}\pi}\right)$$$$~~~~~=-\frac{\,1 \,}{\,2 \,}-\frac{\,\sqrt{3} \,}{\,2 \,}i$$$k=5$ のとき、$$~~~z=1\cdot\left(\cos{\frac{\,5 \,}{\,3 \,}\pi}+i\sin{\frac{\,5 \,}{\,3 \,}\pi}\right)$$$$~~~~~=-\frac{\,1 \,}{\,2 \,}-\frac{\,\sqrt{3} \,}{\,2 \,}i$$

したがって、答えは$$~~~z=1~,~-1$$$$~~~~~~~~,~\frac{\,1 \,}{\,2 \,}+\frac{\,\sqrt{3} \,}{\,2 \,}i~,~-\frac{\,1 \,}{\,2 \,}+\frac{\,\sqrt{3} \,}{\,2 \,}i$$$$~~~~~~~~,~\frac{\,1 \,}{\,2 \,}-\frac{\,\sqrt{3} \,}{\,2 \,}i~,~-\frac{\,1 \,}{\,2 \,}-\frac{\,\sqrt{3} \,}{\,2 \,}i$$まとめると、$$~~~z=\pm1~,~\pm \frac{\,1 \,}{\,2 \,}\pm\frac{\,\sqrt{3} \,}{\,2 \,}i$$となる。