複素数を含む方程式の解

複素数を含む方程式の解の解法
問題解説：複素数を含む方程式の解
今回のまとめ

複素数を含む方程式の解の解法

Point：複素数を含む方程式の解方程式 $z^n=a+bi$ の解は、
① 解 $z$ を、$$~~~z=r(\cos{\theta}+i\sin{\theta})$$とおく。ただし、$r\gt0$
② $z^n$ をド・モアブルの定理より求める。$$~~~z^n=r^n(\cos{n\theta}+i\sin{n\theta})$$③ 右辺の $a+bi$ を極形式で表す。
絶対値 $r’$ 、偏角 $\theta{}’$ より、$$~~~a+bi=r'(\cos{\theta{}’}+i\sin{\theta{}’})$$④ $z^n=a+bi$ より、②と③の式を比較すると、
絶対値は $r^n=r’$
偏角は、三角関数の周期性を考えて、$k$ を整数として、$$~~~n\theta=\theta{}’+2\pi\times k$$⑤ $0≦\theta\lt2\pi$ の範囲に含まれるように $k$ の値を考え $\theta$ を求める。
⑥ $r$ と $\theta$ を①に代入して、$z$ を求める。

問題解説：複素数を含む方程式の解

問題解説(1)

問題次の方程式の解を求めよ。$${\small (1)}~z^4=9$$

$z^4=9$ の解 $z$ を、$$~~~z=r(\cos{\theta}+i\sin{\theta})~~~\cdots~{\large ①}$$とおく。ただし、$r\gt0$
$z^4$ はド・モアブルの定理より、$$~~~z^4=r^4(\cos{4\theta}+i\sin{4\theta})~~~\cdots~{\large ②}$$
また、右辺の $9$ を極形式で表すと、
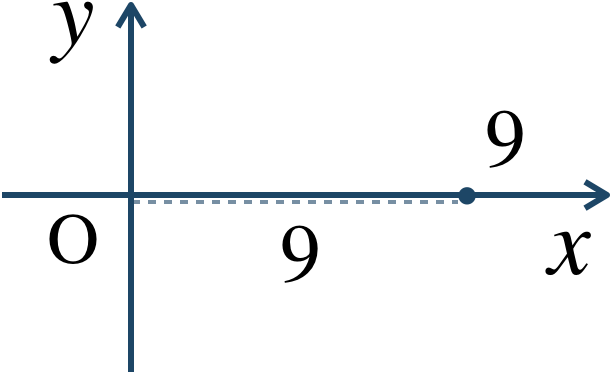
絶対値は、$$~~~\sqrt{9^2+0^2}=\sqrt{9^2}=9$$また、複素数平面上に表すと、

これより、偏角 $0$
よって、$$~~~9=9(\cos{0}+i\sin{0})~~~\cdots~{\large ③}$$$z^4=9$ より、②と③を比較すると、
絶対値は、$r^4=9$
$r\gt0$ であるので、$r=\sqrt{3}$

また、偏角は $k$ を整数として、$$~~~4\theta=0+2\pi \times k$$$$~~~4\theta=2k\pi$$両辺を $4$ で割ると、$$~~~\theta=\frac{\,k \,}{\,2 \,}\pi$$$0≦\theta\lt2\pi$ の範囲で考えると、

$k=0$ のとき、$\theta=0$
$k=1$ のとき、$\theta={\large \frac{\,\pi\,}{\,2\,}}$
$k=2$ のとき、$\theta=\pi$
$k=3$ のとき、$\theta={\large \frac{\,3\,}{\,2\,}}\pi$

よって、それぞれの場合で①に代入し $z$ を求めると、
$k=0$ のとき、$$~~~z=\sqrt{3}(\cos{0}+i\sin{0})$$$$~~~~~=\sqrt{3}(1+i\times 0)=\sqrt{3}$$$k=1$ のとき、$$~~~z=\sqrt{3} \left(\cos{\frac{\,\pi \,}{\,2 \,}}+i\sin{\frac{\,\pi \,}{\,2 \,}}\right)$$$$~~~~~=\sqrt{3}(0+i\times 1)=\sqrt{3}i$$$k=2$ のとき、$$~~~z=\sqrt{3}(\cos{\pi}+i\sin{\pi})$$$$~~~~~=\sqrt{3}(-1+i\times 0)=-\sqrt{3}$$$k=3$ のとき、$$~~~z=\sqrt{3}\left(\cos{\frac{\,3\,}{\,2 \,}\pi}+i\sin{\frac{\,3 \,}{\,2 \,}\pi}\right)$$$$~~~~~=\sqrt{3}\{0+i\times (-1)\}=-\sqrt{3}i$$

したがって、答えは$$~~~z=\sqrt{3}~,~-\sqrt{3}~,~\sqrt{3}i~,~-\sqrt{3}i$$まとめると、$$~~~z=\pm\sqrt{3}~,~\pm \sqrt{3}i$$となる。

問題解説(2)

問題次の方程式の解を求めよ。$${\small (2)}~z^4=-2+2\sqrt{3}i$$

$z^4=-2+2\sqrt{3}i$ の解 $z$ を、$$~~~z=r(\cos{\theta}+i\sin{\theta})~~~\cdots~{\large ①}$$とおく。ただし、$r\gt0$
$z^4$ はド・モアブルの定理より、$$~~~z^4=r^4(\cos{4\theta}+i\sin{4\theta})~~~\cdots~{\large ②}$$
また、右辺の $-2+2\sqrt{3}i$ を極形式で表すと、
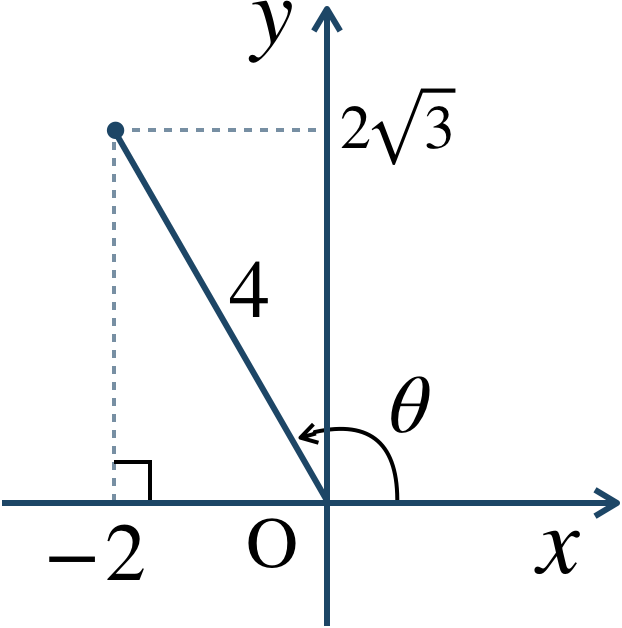
絶対値は、$$~~~~~~|-2+2\sqrt{3}i|$$$$~=\sqrt{(-2)^2+(2\sqrt{3})^2}$$$$~=\sqrt{4+12}=\sqrt{16}=4$$また、複素数平面上に表すと、

これより、偏角 ${\large \frac{\,2\,}{\,3\,}}\pi$
よって、$$~~~4\left(\cos{\frac{\,2 \,}{\,3 \,}\pi}+i\sin{\frac{\,2 \,}{\,3 \,}\pi}\right)~~~\cdots~{\large ③}$$$z^4=-2+2\sqrt{3}i$ より、②と③を比較すると、
絶対値は、$r^4=4$
$r\gt0$ であるので、$r=\sqrt{2}$

また、偏角は $k$ を整数として、$$~~~4\theta=\frac{\,2 \,}{\,3 \,}\pi+2\pi \times k$$両辺を $4$ で割ると、$$~~~\theta=\frac{\,\pi \,}{\,6 \,}+\frac{\,k \,}{\,2 \,}\pi$$$0≦\theta\lt2\pi$ の範囲で考えると、

$k=0$ のとき、$\theta={\large \frac{\,\pi\,}{\,6\,}}$
$k=1$ のとき、$\theta={\large \frac{\,2\,}{\,3\,}}\pi$
$k=2$ のとき、$\theta={\large \frac{\,7\,}{\,6\,}}\pi$
$k=3$ のとき、$\theta={\large \frac{\,5\,}{\,3\,}}\pi$

よって、それぞれの場合で①に代入し $z$ を求めると、
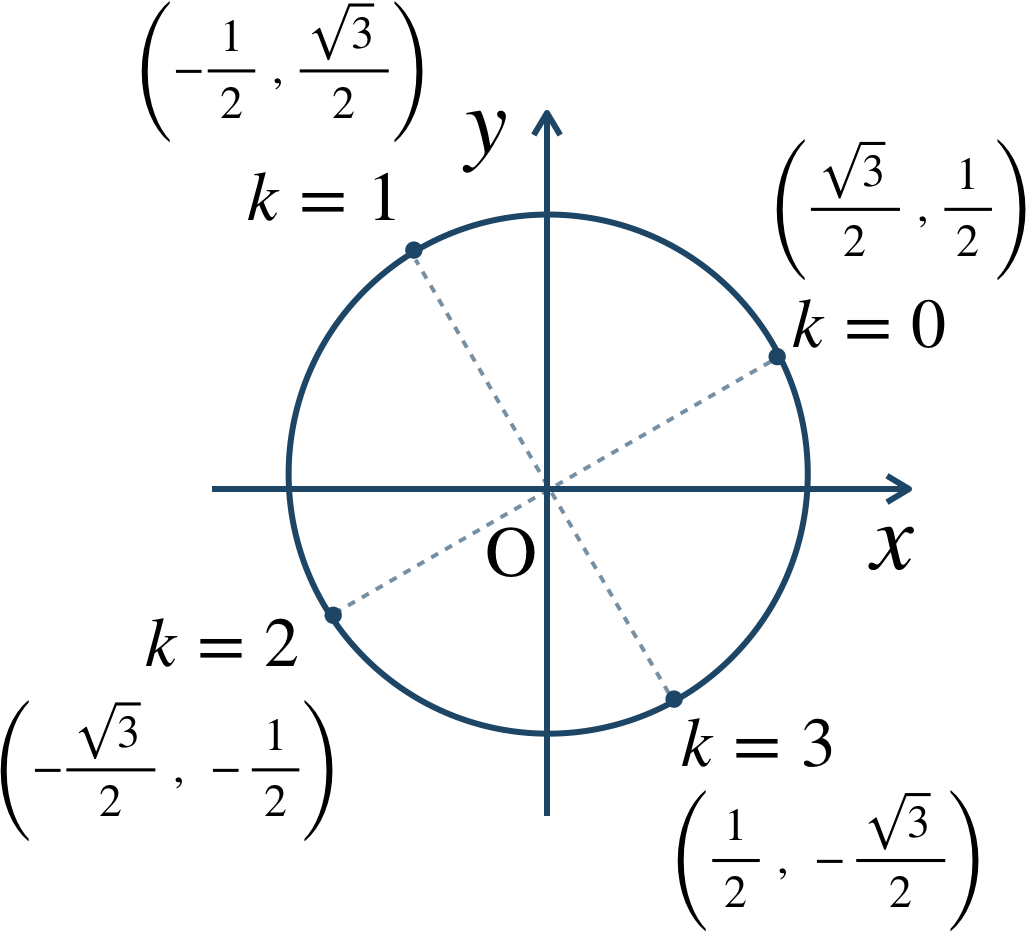
$k=0$ のとき、$$~~~z=\sqrt{2} \left(\cos{\frac{\,\pi \,}{\,6 \,}}+i\sin{\frac{\,\pi \,}{\,6 \,}}\right)$$$$~~~~~=\sqrt{2}\left(\frac{\,\sqrt{3} \,}{\,2 \,}+\frac{\,1 \,}{\, 2\,}i\right)$$$$~~~~~=\frac{\,\sqrt{6} \,}{\,2 \,}+\frac{\,\sqrt{2} \,}{\, 2\,}i$$$k=1$ のとき、$$~~~z=\sqrt{2} \left(\cos{\frac{\,2 \,}{\,3 \,}\pi}+i\sin{\frac{\,2\,}{\,3\,}\pi}\right)$$$$~~~~~=\sqrt{2}\left(-\frac{\,1 \,}{\,2 \,}+\frac{\,\sqrt{3} \,}{\, 2\,}i\right)$$$$~~~~~=-\frac{\,\sqrt{2} \,}{\,2 \,}+\frac{\,\sqrt{6} \,}{\, 2\,}i$$$k=2$ のとき、$$~~~z=\sqrt{2} \left(\cos{\frac{\,7 \,}{\,6 \,}\pi}+i\sin{\frac{\,7\,}{\,6\,}\pi}\right)$$$$~~~~~=\sqrt{2}\left(-\frac{\,\sqrt{3}\,}{\,2 \,}-\frac{\,1\,}{\, 2\,}i\right)$$$$~~~~~=-\frac{\,\sqrt{6} \,}{\,2 \,}-\frac{\,\sqrt{2} \,}{\, 2\,}i$$$k=3$ のとき、$$~~~z=\sqrt{2} \left(\cos{\frac{\,5 \,}{\,3 \,}\pi}+i\sin{\frac{\,5\,}{\,3\,}\pi}\right)$$$$~~~~~=\sqrt{2}\left(\frac{\,1 \,}{\,2 \,}-\frac{\,\sqrt{3} \,}{\, 2\,}i\right)$$$$~~~~~=\frac{\,\sqrt{2} \,}{\,2 \,}-\frac{\,\sqrt{6} \,}{\, 2\,}i$$

したがって、答えは$$~~~z=\frac{\,\sqrt{6} \,}{\,2 \,}+\frac{\,\sqrt{2} \,}{\, 2\,}i~,~-\frac{\,\sqrt{2} \,}{\,2 \,}+\frac{\,\sqrt{6} \,}{\, 2\,}i$$$$~~~~~~~,~-\frac{\,\sqrt{6} \,}{\,2 \,}-\frac{\,\sqrt{2} \,}{\, 2\,}i~,~\frac{\,\sqrt{2} \,}{\,2 \,}-\frac{\,\sqrt{6} \,}{\, 2\,}i$$まとめると、$$~~~z=\pm\frac{\,\sqrt{6} \,}{\,2 \,}\pm\frac{\,\sqrt{2} \,}{\, 2\,}i~,~\mp\frac{\,\sqrt{2} \,}{\,2 \,}\pm\frac{\,\sqrt{6} \,}{\, 2\,}i$$（符号同順）となる。

問題解説(3)

問題次の方程式の解を求めよ。$${\small (3)}~z^3=-8i$$

$z^3=-8i$ の解 $z$ を、$$~~~z=r(\cos{\theta}+i\sin{\theta})~~~\cdots~{\large ①}$$とおく。ただし、$r\gt0$
$z^3$ はド・モアブルの定理より、$$~~~z^3=r^3(\cos{3\theta}+i\sin{3\theta})~~~\cdots~{\large ②}$$
また、右辺の $-8i$ を極形式で表すと、
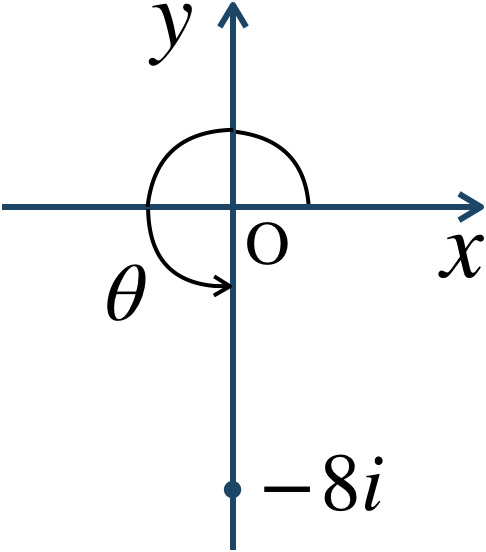
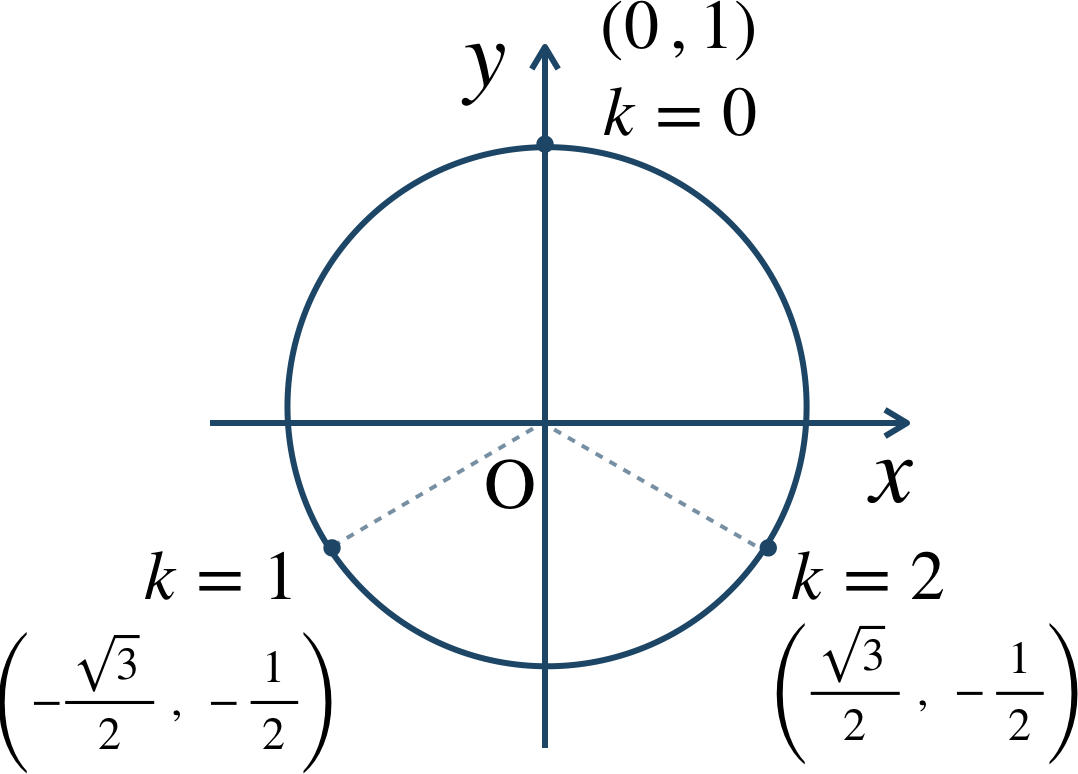
絶対値は、$$~~~|-8i|=\sqrt{0^2+(-8)^2}$$$$~~~~~~~~~~~~~~=\sqrt{8^2}=\sqrt{16}=8$$また、複素数平面上に表すと、

これより、偏角 ${\large \frac{\,3\,}{\,2\,}}\pi$
よって、$$~~~8\left(\cos{\frac{\,3 \,}{\,2 \,}\pi}+i\sin{\frac{\,3 \,}{\,2 \,}\pi}\right)~~~\cdots~{\large ③}$$$z^3=-8i$ より、②と③を比較すると、
絶対値は、$r^3=8$
$r\gt0$ であるので、$r=2$

また、偏角は $k$ を整数として、$$~~~3\theta=\frac{\,3 \,}{\,2 \,}\pi+2\pi \times k$$両辺を $3$ で割ると、$$~~~\theta=\frac{\,\pi \,}{\,2 \,}+\frac{\,2k \,}{\,3 \,}\pi$$$0≦\theta\lt2\pi$ の範囲で考えると、

$k=0$ のとき、$\theta={\large \frac{\,\pi\,}{\,2\,}}$
$k=1$ のとき、$\theta={\large \frac{\,7\,}{\,6\,}}\pi$
$k=2$ のとき、$\theta={\large \frac{\,11\,}{\,6\,}}\pi$

よって、それぞれの場合で①に代入し $z$ を求めると、
$k=0$ のとき、$$~~~z=2 \left(\cos{\frac{\,\pi \,}{\,2 \,}}+i\sin{\frac{\,\pi \,}{\,2\,}}\right)$$$$~~~~~=2(+i\times 1)=2i$$$k=1$ のとき、$$~~~z=2 \left(\cos{\frac{\,7 \,}{\,6 \,}\pi}+i\sin{\frac{\,7\,}{\,6\,}\pi}\right)$$$$~~~~~=2\left(-\frac{\,\sqrt{3}\,}{\,2 \,}-\frac{\,1 \,}{\, 2\,}i\right)=-\sqrt{3}-i$$$k=2$ のとき、$$~~~z=2 \left(\cos{\frac{\,11 \,}{\,6 \,}\pi}+i\sin{\frac{\,11\,}{\,6\,}\pi}\right)$$$$~~~~~=2 \left(\frac{\,\sqrt{3}\,}{\,2 \,}-\frac{\,1\,}{\, 2\,}i\right)=\sqrt{3}-i$$

したがって、答えは$$~~~z=2i~,~-\sqrt{3}-i~,~\sqrt{3}-i$$まとめると、$$~~~z=2i~,~\pm\sqrt{3}-i$$となる。