複素数の表す図形の解法
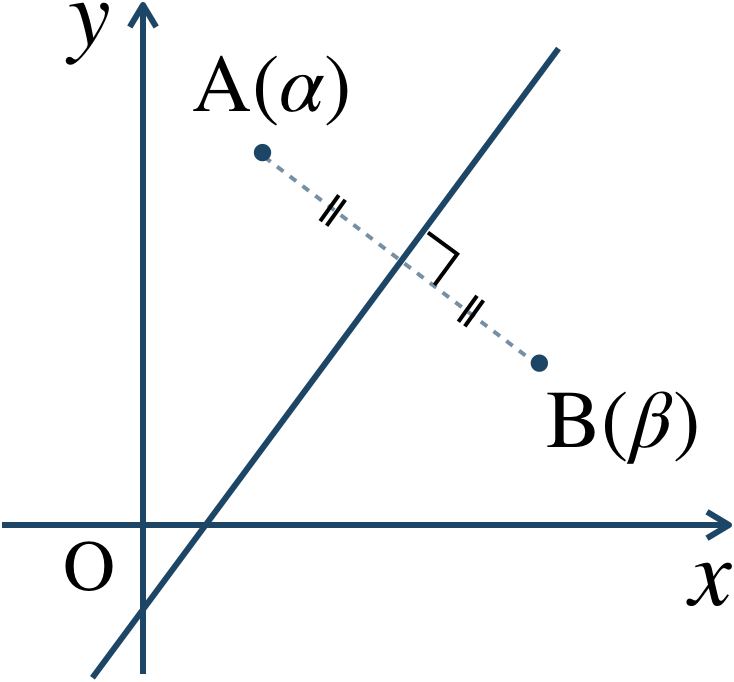
複素数平面上の2点 \({\rm A}(\alpha)~,~{\rm B}(\beta)\) に対して、
この方程式を満たす点 \({\rm P}(z)\) 全体は、線分 \({\rm AB}\) の垂直二等分線となる。
■ 複素数平面上の円
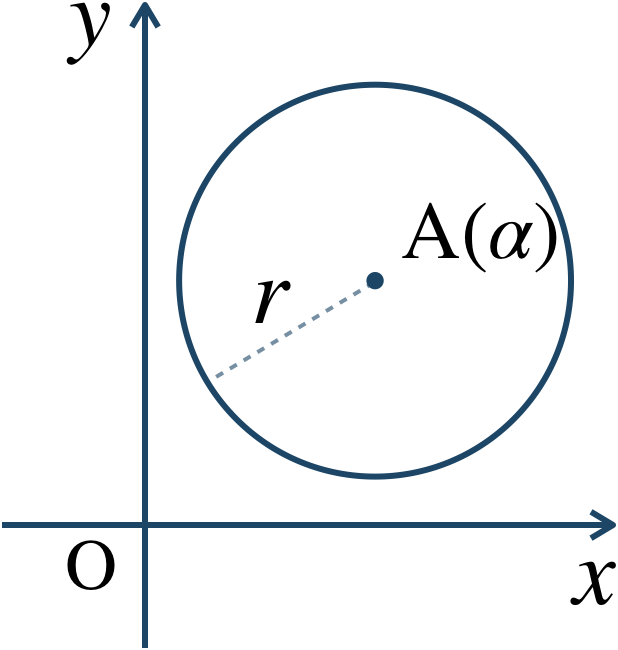
複素数平面上の点 \({\rm A}(\alpha)\) に対して、
この方程式を満たす点 \({\rm P}(z)\) 全体は、点 \({\rm A}(\alpha)\) を中心とする半径 \(r\) の円となる。
問題解説:複素数の表す図形
問題解説(1)
式変形すると、$$~~~|z-2|=\left|z-(1-2i)\right|$$2点 \({\rm A}(2)\) 、\({\rm B}(1-2i)\) とすると、点 \(z\) は2点 \({\rm A}\) 、\({\rm B}\) を結ぶ線分 \({\rm AB}\) の垂直二等分線となる。
問題解説(2)
両辺を \(\div2\) すると、$$~~~\left|z-\frac{\,1 \,}{\,2 \,}\right|=\left|z-\frac{\,1 \,}{\,2 \,}i\right|$$2点 \({\rm A}\left({\large \frac{\,1\,}{\,2\,}}\right)\) 、\({\rm B}\left({\large \frac{\,1\,}{\,2\,}}i\right)\) とすると、点 \(z\) は2点 \({\rm A}\) 、\({\rm B}\) を結ぶ線分 \({\rm AB}\) の垂直二等分線となる。
問題解説(3)
式変形すると、$$~~~\left|z-(2-3i)\right|=3$$点 \({\rm A}(2-3i)\) とすると、点 \(z\) は \({\rm A}\) を中心とする半径 \(3\) の円となる。
問題解説(4)
与えられた式より、$$~~~(2z+3i)\left(2\overline {z}-3i\right)=16$$これは \(-3i=\overline {3i}\) より、$$~~~(2z+3i)\left(\overline {2z+3i}\right)=16$$複素数の性質 \(z\overline {z}=|z|^2\) より、$$~~~|2z+3i|^2=16$$\(16=4^2\) より、$$~~~|2z+3i|=4$$両辺を \(\div2\) すると、$$~~~~~~~~~~~\left|z+\frac{\,3 \,}{\,2 \,}i\right|=2$$$$~~~\left|z-\left(-\frac{\,3 \,}{\,2 \,}i\right)\right|=2$$点 \({\rm A}\left(-{\large \frac{3}{2}}i\right)\) とすると、点 \(z\) は \({\rm A}\) を中心とする半径 \(2\) の円となる。
今回のまとめ
複素数の表す図形について解説しました。方程式の形から複素数平面上のどのような図形となるかを読み取れるようになりましょう。