複素数平面上の複素数の和・差

2020.09.092020.09.14

複素数平面上の複素数の和・差の解法
問題解説：複素数平面上の複素数の和・差
今回のまとめ

複素数平面上の複素数の和・差の解法

Point：複素数平面上の複素数の和・差２つの複素数 $\alpha=a+bi~,~\beta=c+di$ において、
■ 複素数の和

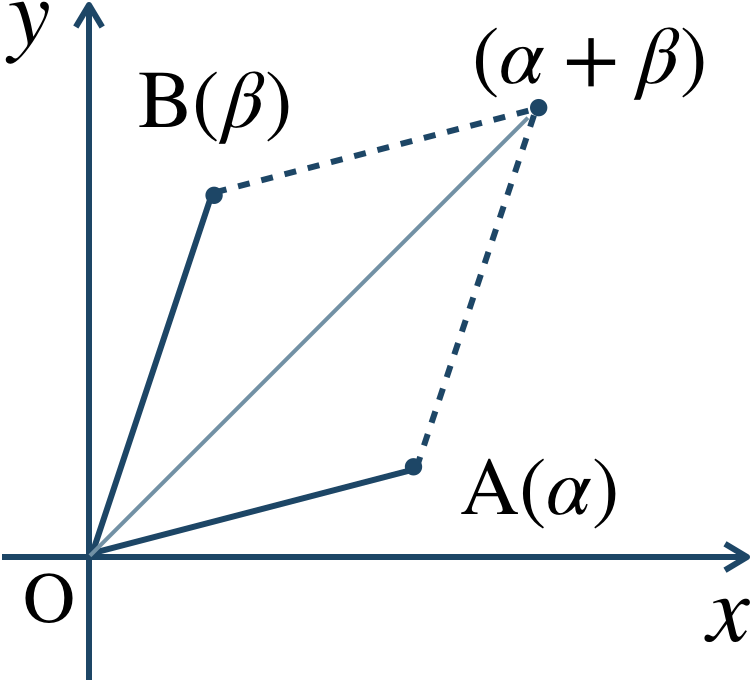
２つの複素数の和(加法)は、$$~~~~~~\alpha+\beta$$$$~=(a+bi)+(c+di)$$$$~=(a+c)+(b+d)i$$図のように、平行四辺形をつくり、原点と対角線上にあるの点となる。

■ 複素数の差

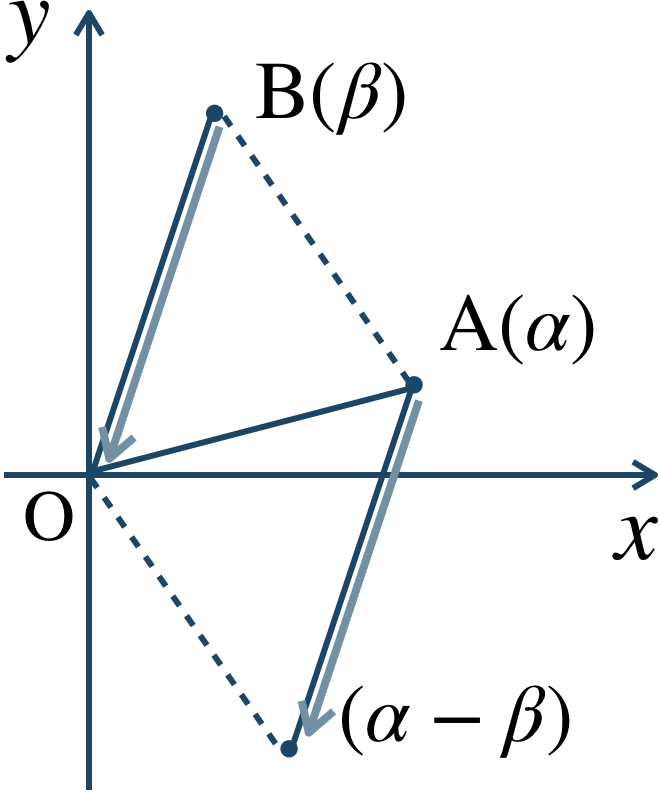
２つの複素数の差(減法)は、$$~~~~~~\alpha-\beta$$$$~=(a+bi)-(c+di)$$$$~=(a-c)+(b-d)i$$図のように、点 ${\rm B}$ が原点まで平行移動するのと同様に、点 ${\rm A}$ を平行移動した点となる。

問題解説：複素数平面上の複素数の和・差

問題解説(1)

問題次の図の複素数平面上の２点 ${\rm A}(\alpha)~,~{\rm B}(\beta)$ について、次の複素数を求め図示せよ。

$${\small (1)}~\alpha+\beta$$

図より、$$~~~~~~\alpha=2+3i~,~\beta=3-i$$となる。
よって、与えられた式を計算すると、$$~~~~~~\alpha+\beta$$$$~=(2+3i)+(3-i)$$$$~=5+2i$$よって、答えは $5+2i$ となる。
また、図は ${\rm OA~,~OB}$ を辺とする平行四辺形の対角線の点となる。

問題解説(2)

問題次の図の複素数平面上の２点 ${\rm A}(\alpha)~,~{\rm B}(\beta)$ について、次の複素数を求め図示せよ。

$${\small (2)}~\alpha-\beta$$

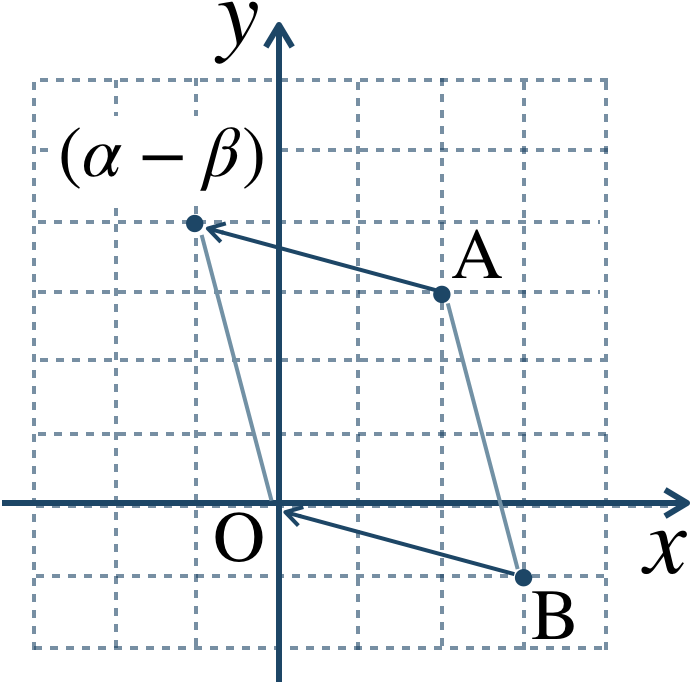
与えられた式を計算すると、$$~~~~~~\alpha-\beta$$$$~=(2+3i)-(3-i)$$$$~=2+3i-3+i$$$$~=-1+4i$$よって、答えは $-1+4i$ となる。
また、図は点 ${\rm B}$ を原点まで平行移動するのと同様に点 ${\rm A}$ を平行移動した点となる。

問題解説(3)

問題次の図の複素数平面上の２点 ${\rm A}(\alpha)~,~{\rm B}(\beta)$ について、次の複素数を求め図示せよ。

$${\small (3)}~\beta-\alpha$$

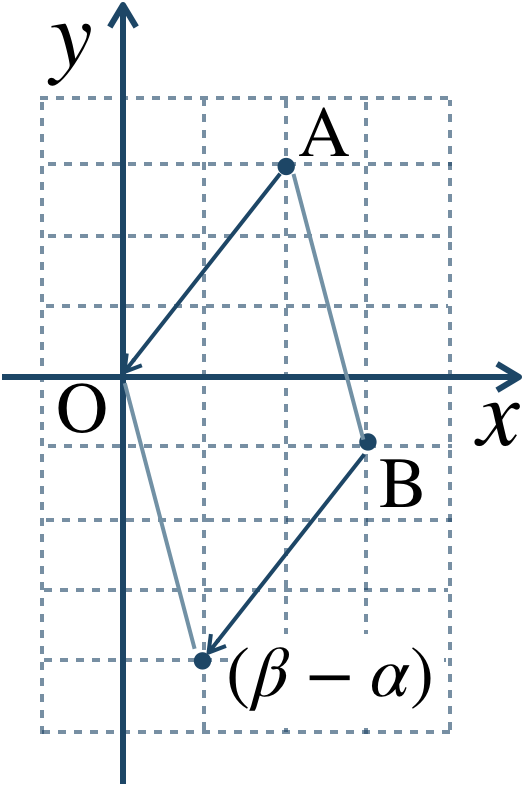
与えられた式を計算すると、$$~~~~~~\beta-\alpha$$$$~=(3-i)-(2+3i)$$$$~=3-i-2-3i$$$$~=1-4i$$よって、答えは $1-4i$ となる。
また、図は点 ${\rm A}$ を原点まで平行移動するのと同様に点 ${\rm B}$ を平行移動した点となる。

問題解説(4)

問題次の図の複素数平面上の２点 ${\rm A}(\alpha)~,~{\rm B}(\beta)$ について、次の複素数を求め図示せよ。

$${\small (4)}~\alpha+2\beta$$

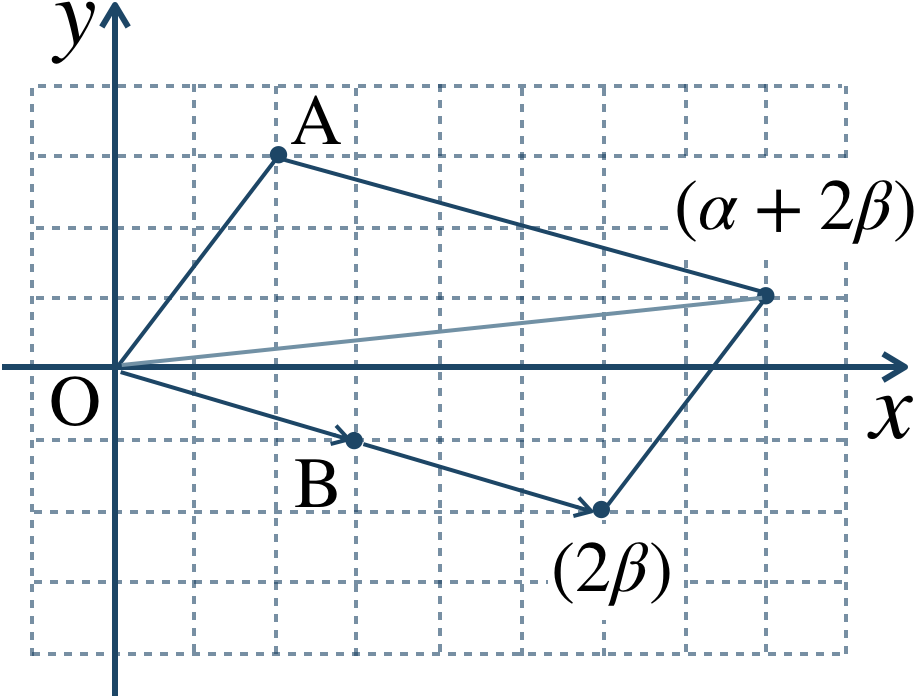
与えられた式を計算すると、$$~~~~~~\alpha+2\beta$$$$~=(2+3i)+2(3-i)$$$$~=2+3i+6-2i$$$$~=8+i$$よって、答えは $8+i$ となる。
また、図は点${\rm B}$ の原点からの２倍の位置の点と点 ${\rm A}$ とでつくる平行四辺形の対角線の点となる。