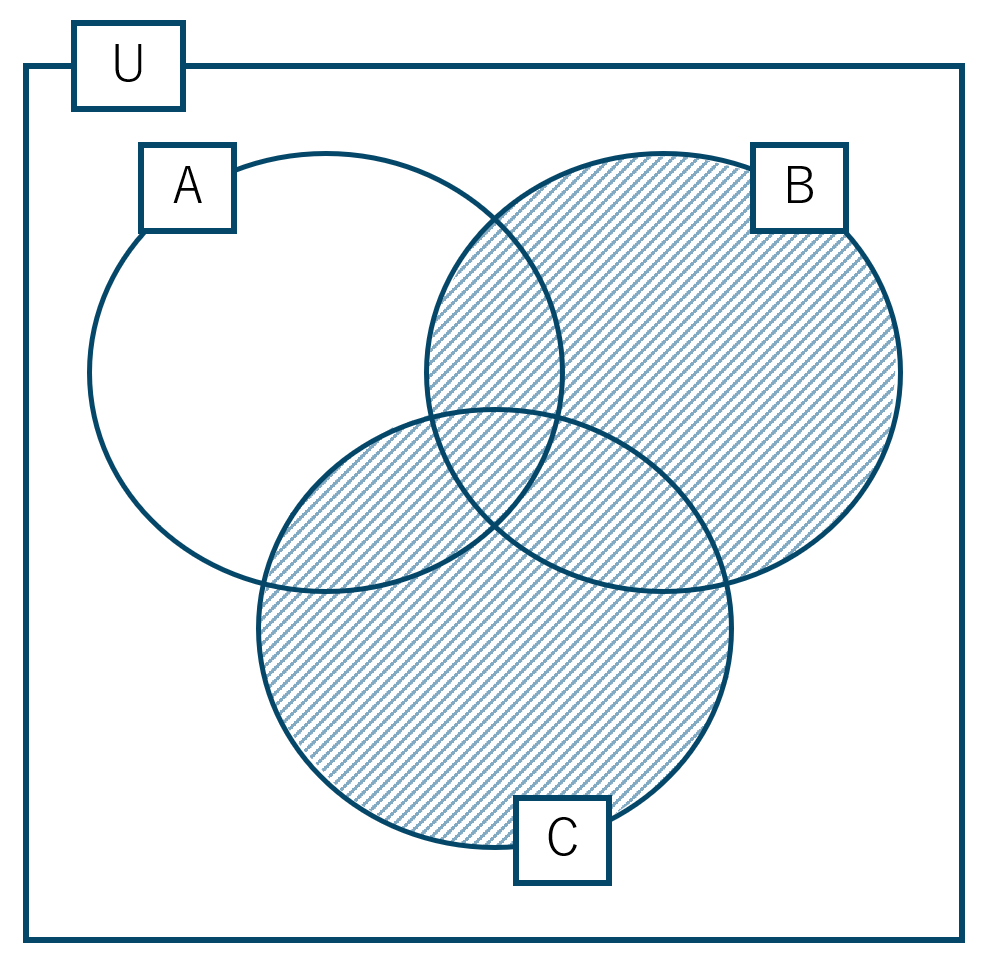
３つの集合の要素の個数

３つの集合の要素の個数の求め方
問題解説：３つの集合の要素の個数
今回のまとめ

３つの集合の要素の個数の求め方

Point：３つの集合の要素の個数$n({\rm A} \cup {\rm B} \cup {\rm C})$ は次のベン図の斜線部分を表します。

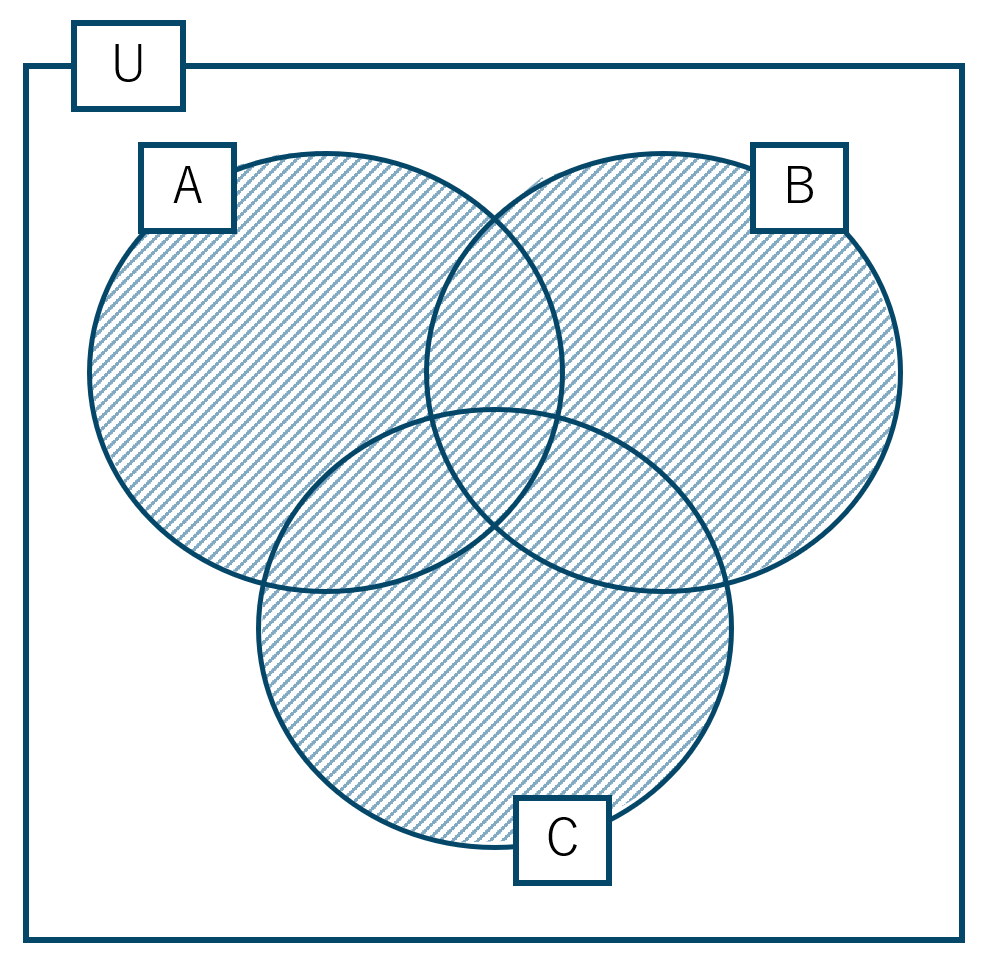
まず $n({\rm A})+n({\rm B})+n({\rm C})$ を考えると、次のように２回カウントしている部分と３回カウントしている部分が出てきます。

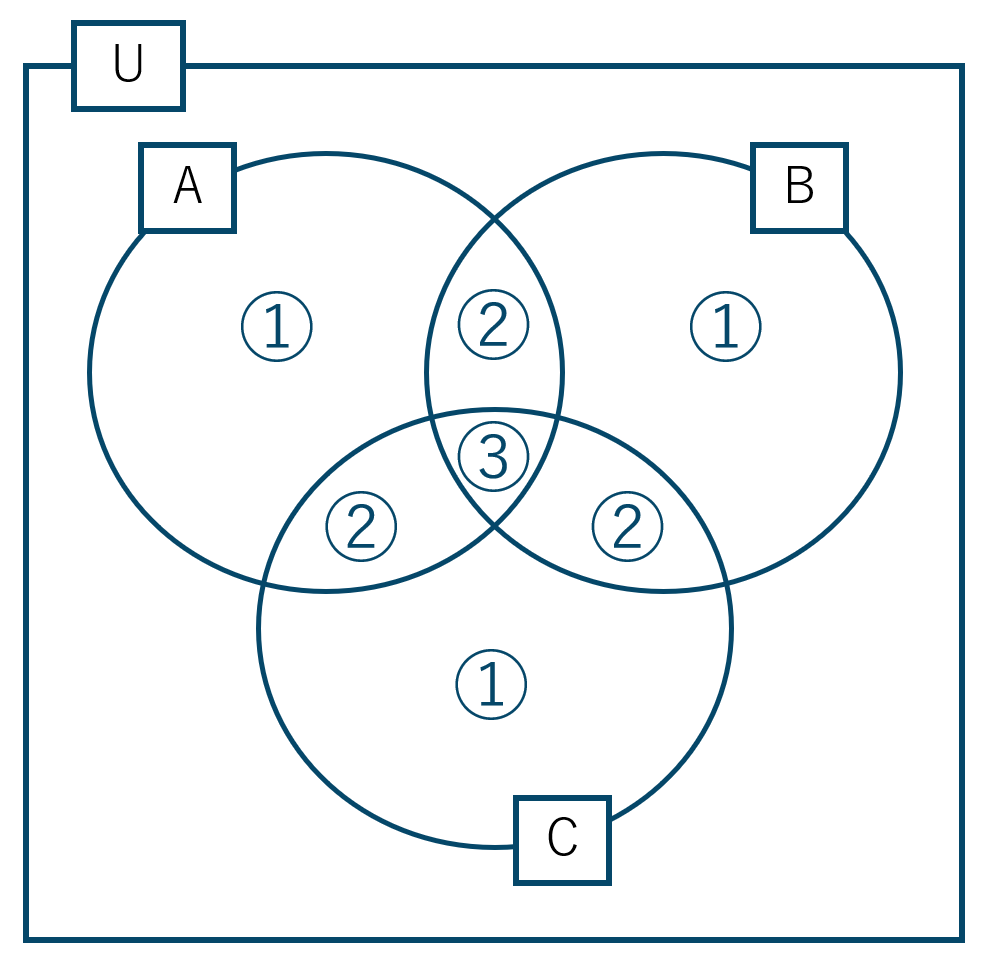
次にそれぞの共通部分を引くと、$$~n({\rm A})+n({\rm B})+n({\rm C})$$$$~~~~~~~-n({\rm A} \cap {\rm B})-n({\rm B} \cap {\rm C})-n({\rm A} \cap {\rm C})$$ベン図では、

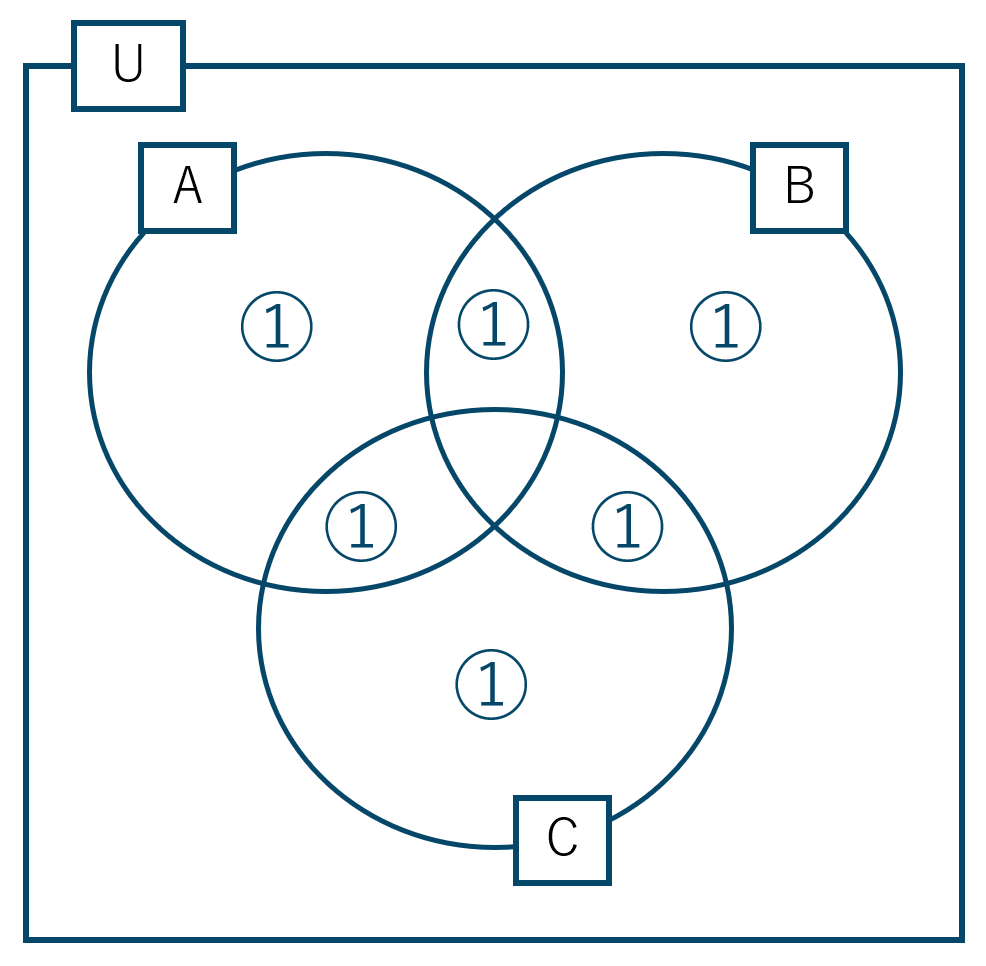
よって、$n({\rm A} \cap {\rm B} \cap {\rm C})$ の部分は３回引かれたことになり、カウントが０回になります。
これより $n({\rm A} \cap {\rm B} \cap {\rm C})$ を１回加えると、ベン図は次のようになります。

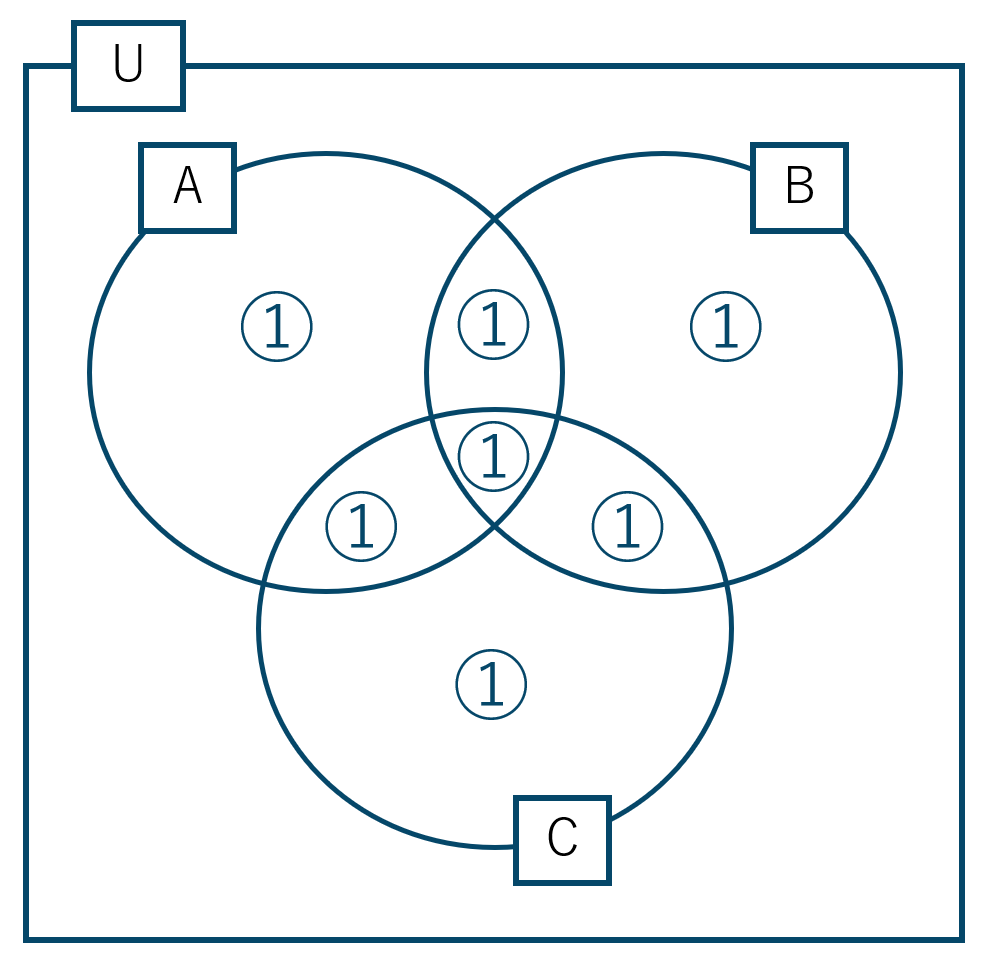
よって、

$$~~~n({\rm A} \cup {\rm B} \cup {\rm C})$$$$=n({\rm A})+n({\rm B})+n({\rm C})$$$$~~~~-n({\rm A} \cap {\rm B})-n({\rm B} \cap {\rm C})-n({\rm A} \cap {\rm C})~$$$$~~~~~~+n({\rm A} \cap {\rm B} \cap {\rm C})$$

問題解説：３つの集合の要素の個数

問題1～100までの自然数のうち、２の倍数の集合を $\rm A$、３の倍数の集合を $\rm B$ とするとき、５の倍数の集合を $\rm C$ とするとき、次の値を求めよ。

まずはそれぞれの集合の要素の個数を求めておきましょう。
２の倍数の集合 $\rm A$ は、$${\rm A}=\{~2\times 1~,~2\times 2~,~2\times 3~,~\cdots~,~2\times 50~\}$$これより、$n({\rm A})=50$ となります。

３の倍数の集合 $\rm B$ は、$${\rm B}=\{~3\times 1~,~3\times 2~,~3\times 3~,~\cdots~,~3\times 33~\}$$これより、$n({\rm B})=33$ となります。

５の倍数の集合 $\rm C$ は、$${\rm C}=\{~5\times 1~,~5\times 2~,~5\times 3~,~\cdots~,~5\times 20~\}$$これより、$n({\rm C})=20$ となります。

また、それぞれの共通部分の要素の個数は、
${\rm A} \cap {\rm B}$ は２の倍数かつ３の倍数であることより、６の倍数の集合となるので、$${\rm A} \cap {\rm B}=\{~6\times 1~,~6\times 2~,~\cdots~,~6\times 16~\}$$これより、$n({\rm A} \cap {\rm B})=16$ となります。

${\rm B} \cap {\rm C}$ は３の倍数かつ５の倍数であることより、15の倍数の集合となるので、$${\rm B} \cap {\rm C}=\{~15\times 1~,~15\times 2~,~\cdots~,~15\times 6~\}$$これより、$n({\rm B} \cap {\rm C})=6$ となります。

${\rm A} \cap {\rm C}$ は２の倍数かつ５の倍数であることより、10の倍数の集合となるので、$${\rm A} \cap {\rm C}=\{~10\times 1~,~10\times 2~,~\cdots~,~10\times 10~\}$$これより、$n({\rm A} \cap {\rm C})=10$ となります。

さらに、$n({\rm A} \cap {\rm B} \cap {\rm C})$ は２の倍数かつ３の倍数かつ５の倍数であることより、30の倍数の集合となるので、$${\rm A} \cap {\rm B} \cap {\rm C}=\{~30\times 1~,~30\times 2~,~30\times 3~\}$$これより、$n({\rm A} \cap {\rm B} \cap {\rm C})=3$ となります。

問題解説(1)

問題1～100までの自然数のうち、２の倍数の集合を $\rm A$、３の倍数の集合を $\rm B$ とするとき、５の倍数の集合を $\rm C$ とするとき、次の値を求めよ。$${\small (1)}~n({\rm A} \cap {\rm C})$$

２の倍数かつ５の倍数は、10の倍数を表します。
よって、$${\rm A} \cap {\rm C}=\{~10\times 1~,~10\times 2~,~\cdots~,~10\times 10~\}$$答えは $n({\rm A} \cap {\rm C})=10$ となります。

問題解説(2)

問題1～100までの自然数のうち、２の倍数の集合を $\rm A$、３の倍数の集合を $\rm B$ とするとき、５の倍数の集合を $\rm C$ とするとき、次の値を求めよ。$${\small (2)}~n({\rm B} \cup {\rm C})$$

３の倍数または５の倍数は、$n({\rm B} \cup {\rm C})$ と表されてベン図は次のようになります。

よって、$n({\rm B})$ と $n({\rm C})$ を合わせたものから $n({\rm B}\cap {\rm C})$ を１回引けばよいので、$$~~~n({\rm B} \cup {\rm C})=n({\rm B})+n({\rm C})-n({\rm B} \cap {\rm C})$$$$\hspace{50pt}=33+20-6$$$$\hspace{50pt}=47$$ 答えは $n({\rm B} \cup {\rm C})=47$ となります。

問題解説(3)

問題1～100までの自然数のうち、２の倍数の集合を $\rm A$、３の倍数の集合を $\rm B$ とするとき、５の倍数の集合を $\rm C$ とするとき、次の値を求めよ。$${\small (3)}~n({\rm A} \cap {\rm B} \cap {\rm C})$$

２の倍数かつ３の倍数かつ５の倍数は30の倍数を表します。
よって、$${\rm A} \cap {\rm B} \cap {\rm C}=\{~30\times 1~,~30\times 2~,~30\times 3~\}$$答えは $n({\rm A} \cap {\rm B} \cap {\rm C})=3$ となります。

問題解説(4)

問題1～100までの自然数のうち、２の倍数の集合を $\rm A$、３の倍数の集合を $\rm B$ とするとき、５の倍数の集合を $\rm C$ とするとき、次の値を求めよ。$${\small (4)}~n({\rm A} \cup {\rm B} \cup {\rm C})$$

２の倍数または３の倍数または５の倍数は、$n({\rm A} \cup {\rm B} \cup {\rm C})$ と表されます。
よって、公式より、$$~~~~~~n({\rm A} \cup {\rm B} \cup {\rm C})$$$$~=n({\rm A})+n({\rm B})+n({\rm C})$$$$~~~~~~-n({\rm A} \cap {\rm B})-n({\rm B} \cap {\rm C})-n({\rm A} \cap {\rm C})$$$$~~~~~~~~~+n({\rm A} \cap {\rm B} \cap {\rm C})$$$$~=50+33+20-16-6-10+3$$$$~=74$$答えは $n({\rm A} \cup {\rm B} \cup {\rm C})=74$ となります。