２つのグループに分ける

２つのグループに分ける方法

Point：２つのグループに分ける・\(n\) 人を２つのグループＡ、Ｂに分ける
\(n\) 人のそれぞれがＡまたはＢの２通りの選択肢があるので、\(2^n\) 通りとなります。
ただし、これには \(n\) 人がすべてＡに分けられるときとＢに分けられるときの \(2\) 通りを含みます。
 
・\(n\) 人を２つのグループに分ける
この場合は、グループに区別がありません。このときの解法の手順は、
① グループに区別があると考えて場合の数を求めます。
② グループに区別がないので、①で求めた式を(グループの数)！で割ります。
 
例えばの５つの数字 1,2,3,4,5 をＡとＢの２つのグループに分けるとき、

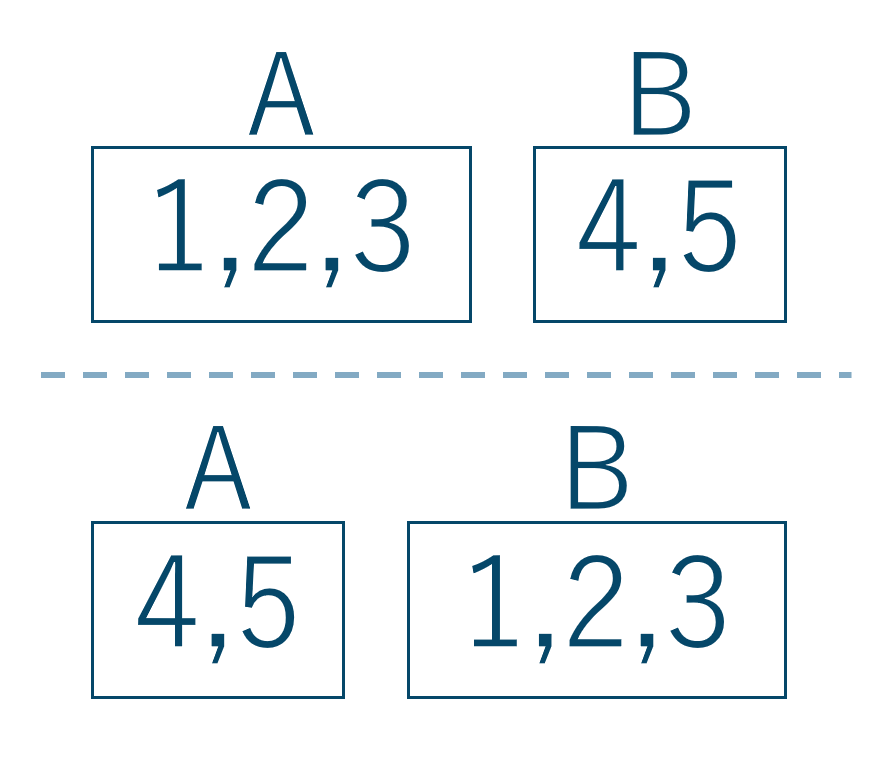
この２つのグループは別々の場合の数です。しかしＡ、Ｂのグループの区別をなくしてしまうと、

このように上と下では同じ分け方になってしまいます。よって、(グループの数)!で割りましょう。

問題解説：２つのグループに分ける

問題解説(1)

すべての人がＡかＢのどちらかを自由に選べます。一人目がＡかＢかの２通りの選び方があり、二人目以降も同じように２通りの選び方があります。よって、$$~~~2^{9}=2^{10} \div 2=1024 \div 2=512$$よって、答えは512通りとなります。
 
（この計算で使った \( 2^{10}=1024 \) は暗記しておきましょう。）

問題解説(2)

空室があってよいと考えて計算していきます。答えは、(1)と同じとなり、$$~~~2^{9}=512$$よって512通りとなります。
次に空室があってはいけないので、
・すべての人がＡに入ってＢが空室
・すべての人がＢに入ってＡが空室
この２通りがダメなパターンとなります。
したがってこの２通りを引いて$$~~~512-2=510$$
よって、答えは510通りとなります。

問題解説(3)

グループに区別があると考えて計算するので、(2)の答えより510通りとなります。
次に、ＡとＢの２つのグループに区別がなくなるので、(グループの数)!の\( 2! \) で割ります。$$~~~510 \div 2!=\frac{510}{2\times 1}=255$$
よって、答えは255通りとなります。

今回のまとめ

問題自体は非常にシンプルですが、解法が少し特殊です。グループに区別があるかないかで、解法が変わってきます。特に(3)のグループの区別がないパターンはしっかりと習得しましょう！

【問題一覧】数学Ａ：場合の数と確率

このページは「高校数学Ａ：場合の数と確率」の問題一覧ページとなります。解説の見たい単元名がわからない...

yorikuwa.com