図形と組合せ
\(n\) 個の頂点から三角形の頂点となる3つを選べばよいので、
で求めることができます。
・正n角形の頂点を結んでできる対角線の本数
\(n\) 個の頂点から線分の端となる2つを選べばよいが、これは正n角形の \(n\) 本の辺も含むので、
で求めることができます。
問題解説:図形と組合せ
問題解説(1)
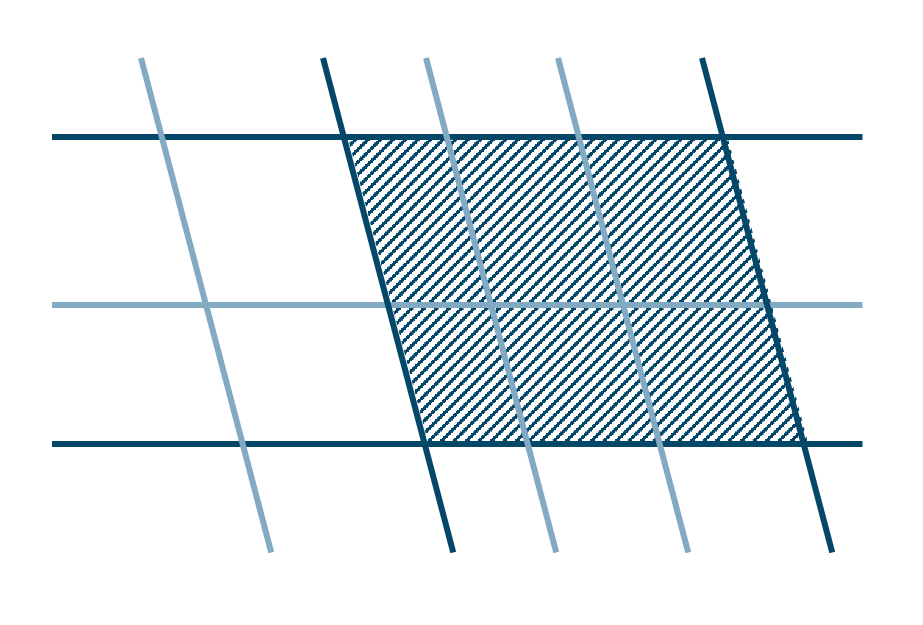
\({\small (1)}~\)5本の平行線と、それとは別の3本の平行線とが交わってできる平行四辺形の数
縦に平行線が5本並んでおり、それとは別の平行線が横に3本並んでいると考えます。
この内部に平行四辺形を作るためには、
このように縦から2本、横からも2本選べば1つの平行四辺形ができます。また平行線の選び方を変えると、
このように選び方が1つに決まればそれに対する平行四辺形がただ1つに決まります。
よって縦の5本のなかから2本選ぶ組合せは、$$~~~{}_{5}{\rm C}_{2}=\frac{5 \times 4}{2 \times 1}=10$$次に横の3本のなかから2本を選ぶ組合せは、$$~~~{}_{3}{\rm C}_{2}=\frac{3 \times 2}{2 \times 1}=3$$この2つの場合の数は「連続して起こる」ので、積の法則より$$~~~10 \times 3 =30$$よって答えは、30通りとなります。
問題解説(2)
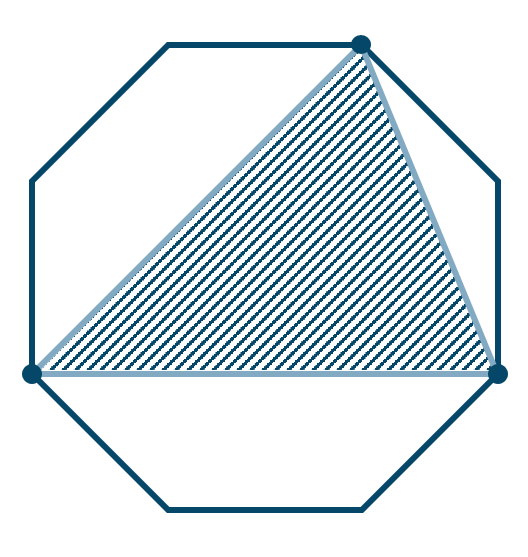
\({\small (2)}~\)正八角形について、頂点を結んでできる三角形の個数
三角形を作るためには3つの頂点が必要になります。よって正八角形の8つの頂点から3つを選べば1つの三角形ができるので、
計算式は、$$~~~{}_{8}{\rm C}_{3}=\frac{8 \times 7 \times 6}{3 \times 2 \times 1}=56$$よって、答えは56通りとなります。
問題解説(3)
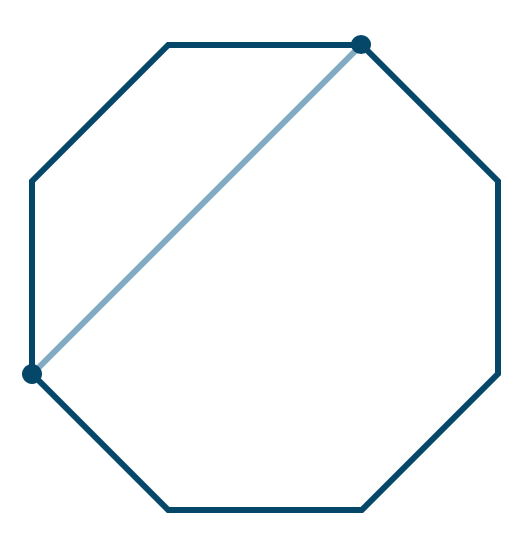
\({\small (3)}~\)正八角形について、頂点を結んでできる対角線の本数
8つの頂点から2つの頂点を選べば線分が1本できます。
計算式は、$$~~~{}_{8}{\rm C}_{2}=\frac{8 \times 7 }{2 \times 1}=28$$ただし、これは正八角形の8本の辺を含んでいるので、$$~~~28-8=20$$よって、答えは20通りとなります。
今回のまとめ
今回は図形を作る問題ですが、その作り方によって組合せの問題になるパターンを学習しました。どのような組合せを考えれば図形ができるかをしっかりと理解しましょう。