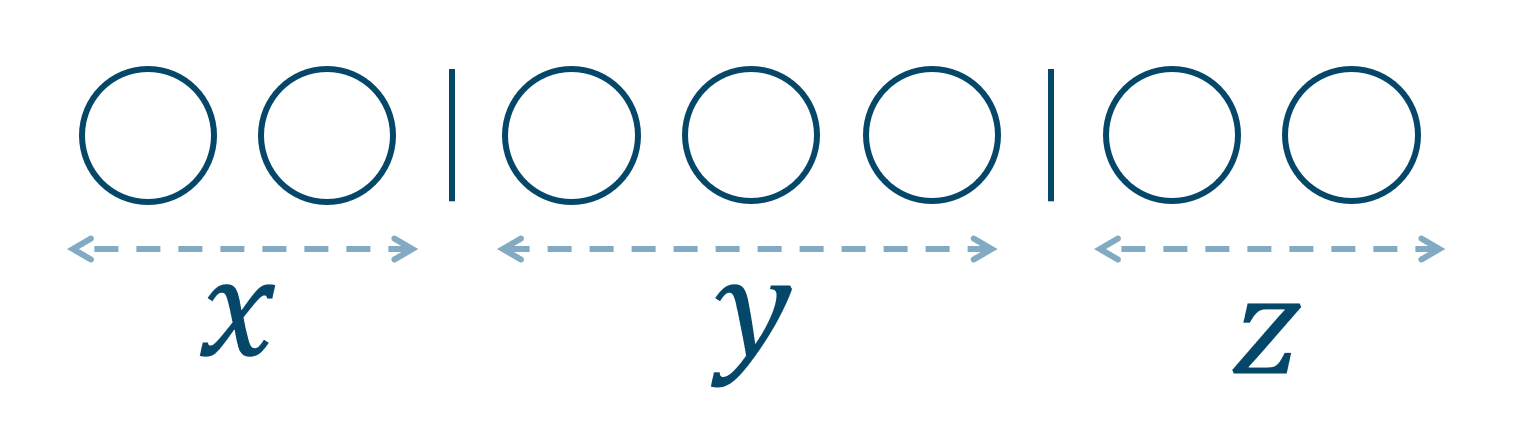等式を満たす自然数の組合せ

2018.03.192020.06.09

問題解説：等式を満たす自然数の組合せ
1. 問題解説(1)
2. 問題解説(2)
今回のまとめ

問題解説：等式を満たす自然数の組合せ

問題解説(1)

問題次の場合の数を求めよ。
${\small (1)}~$$ x+y+z=7$ を満たす $ 0$ 以上の整数の組合せは何通りあるか答えよ。

整数 $ 7$ を「◯」７つとします。また、$ x~,~y~,~z$ の３種類に分けるので、仕切り「 | 」を２つの合計９つのものの順列を考える。
例えば

このとき、 $ x=2~,~y=3~,~z=2$ となります。
また、

このとき、 $ x=4~,~y=0~,~z=3$ となります。

これらより、問題を考えると「◯」が７つと仕切り「 | 」が２つの合計９つのものの同じものを含む順列として計算すると、$$~~~~~~\frac{9!}{7!\cdot 2!}$$$$~=\frac{9\cdot 8}{2\cdot 1}$$$$~=36$$よって、答えは $36$ となります。

問題解説(2)

問題次の場合の数を求めよ。
${\small (2)}~$$ x+y+z=7$ を満たす自然数の組合せは何通りあるか答えよ。

(1)と違い条件が自然数となっています。これより $ x~,~y~,~z$ はそれぞれ少なくとも $ 1$ にはなります。
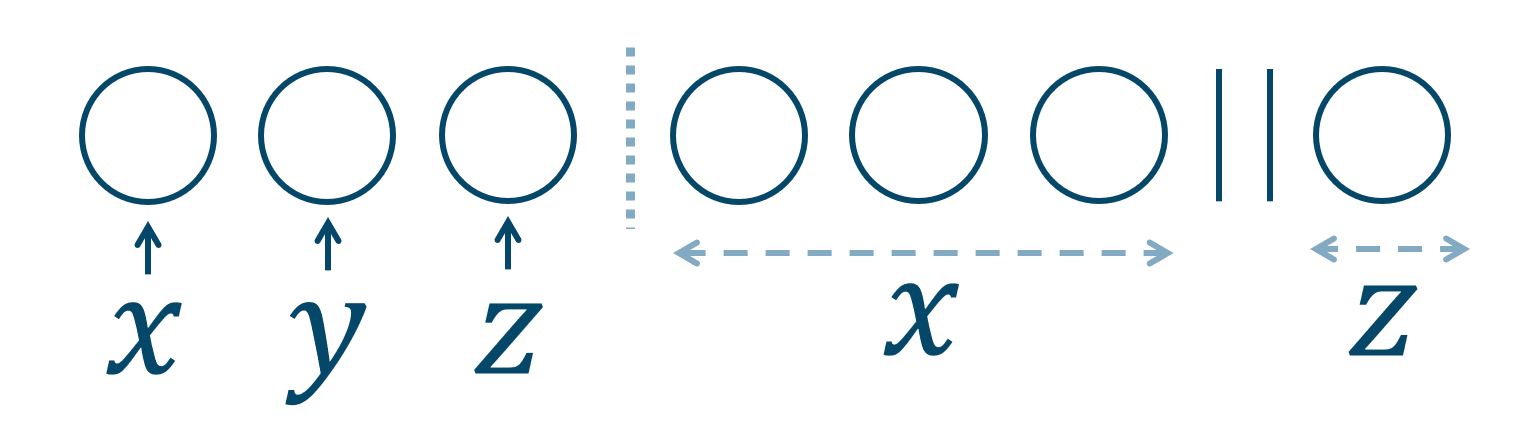
(1)と同じ考え方をすると、 $ x~,~y~,~z$ は初めからそれぞれ「◯」を１つずつ割り当てられている考えればよいです。

例えば、

このとき、$ x=4~,~y=1~,~z=2$ となります。

よって、割り当てられた「◯」３つ以外の残りの「◯」４つと、仕切り「 | 」２つの６つのものの同じものを含む順列として計算すると、$$~~~~~~\frac{6!}{4!\cdot 2!}$$$$~=\frac{6\cdot 5}{2\cdot 1}$$$$~=15$$よって、答えは $15$ となります。