和事象と排反事象の解法
この2つの事象の共通部分が存在しないとき、これらを互いに排反といいます。
このとき、この2つの和事象の確率は、
で求めることができます。
また、この2つの事象の共通部分 \(\rm A\cap B\) が存在するとき、
この2つの和事象の確率は、
で求めることができます。
問題解説:和事象と排反事象
問題解説(1)
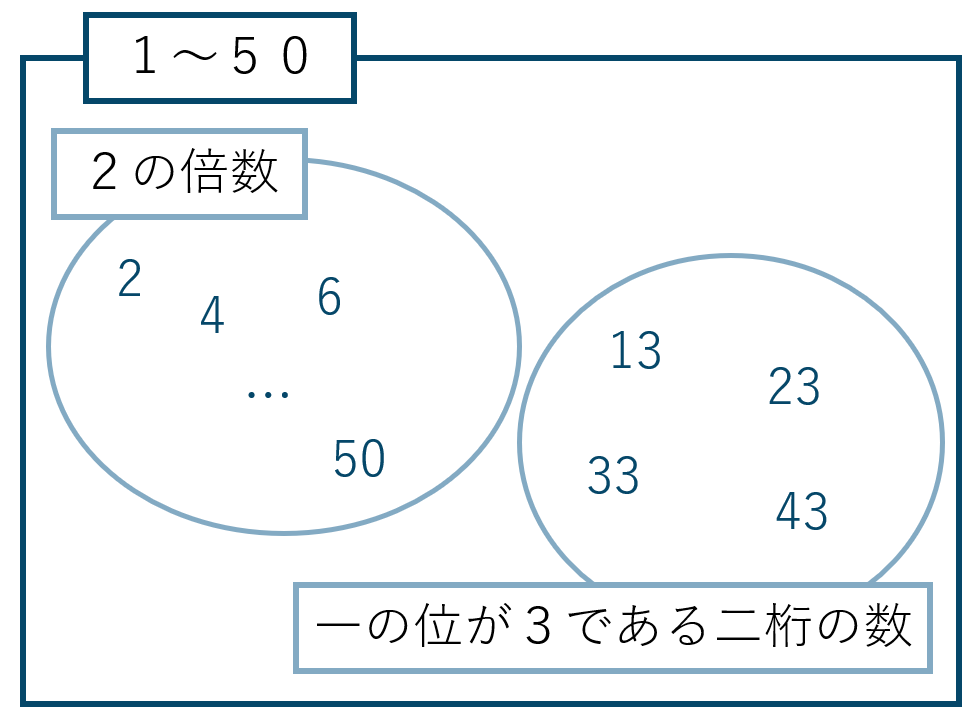
\({\small (1)}~\)2の倍数または一の位が3である2桁の数
すべての場合の数は50枚のカードから1枚だけ取り出すので、50通りとなります。
次に「2の倍数」と「一の位が3である二桁の数」は互いに排反である。
ベン図より、これらは同時に起こらないのでそれぞれの確率のたし算で求まります。
(ⅰ) 2の倍数
倍数の数え方より$$~~~\{~2\times1~,~2\times2~,~2\times3~,~\cdots~,~2\times25~\}$$よって、25通りとなり確率は \( {\Large \frac{25}{50}} \) となります。
(ⅱ) 一の位が3である二桁の数
条件に当てはまるのは、$$~~~\{~13~,~23~,~33~,~43~\}$$よって、4通りとなり確率は \( {\Large \frac{4}{50}} \) となります。
したがって求める確率は、互いに排反であることより$$~~~\frac{25}{50}+\frac{4}{50}=\frac{29}{50}$$答えは \( {\Large \frac{29}{50}} \) となります。
※ここで計算のポイントとして、それぞれの確率は約分せずにそのまま計算しましょう。約分をしてしまうと、その後の計算で通分が必要となり二度手間になってしまうからです。
問題解説(2)
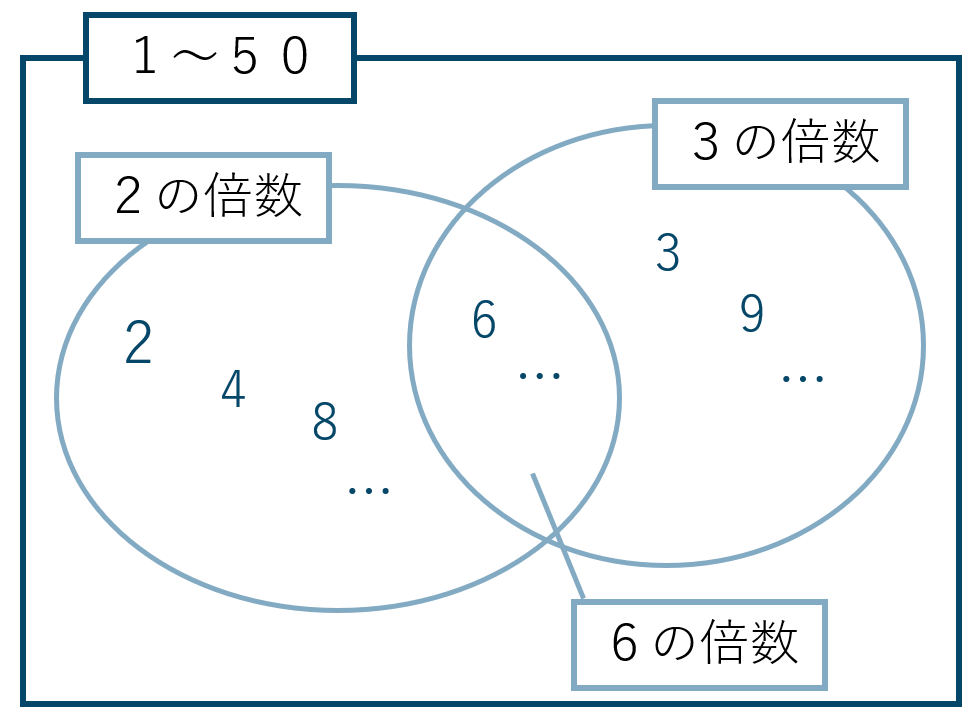
\({\small (2)}~\)2の倍数または3の倍数
すべての場合の数は(1)と同様に50通りとなります。
次に「2の倍数」と「3の倍数」は互いに排反ではありません。これらが同時に起こる「6の倍数」があるからです。したがって求め方が違います。
ベン図より「2の倍数」と「3の倍数」のたし算だけでは求まりません。この2つの共通部分の「6の倍数」を2回カウントしてしまっているからです。よって1回「6の倍数」を引く必要があります。
まずはそれぞれの確率を求めましょう。
(ⅰ) 2の倍数
倍数の数え方より$$~~~\{~2\times1~,~2\times2~,~2\times3~,~\cdots~,~2\times25~\}$$よって、25通りとなり確率は \( {\Large \frac{25}{50}} \) となります。
(ⅱ) 3の倍数
倍数の数え方より$$~~~\{~3\times1~,~3\times2~,~3\times3~,~\cdots~,~3\times16~\}$$よって、16通りとなり確率は \( {\Large \frac{16}{50}} \) となります。
(ⅲ) 6の倍数
倍数の数え方より$$~~~\{~6\times1~,~6\times2~,~6\times3~,~\cdots~,~6\times8~\}$$よって、8通りとなり確率は \( {\Large \frac{8}{50}} \) となります。
以上より求める確率は、$$~~~\frac{25}{50}+\frac{16}{50}-\frac{8}{50}=\frac{33}{50}$$答えは \( {\Large \frac{33}{50}} \) となります。
ここでもそれぞれの確率は約分せずにそのままで計算を進めましょう。
今回のまとめ
和事象の確率は、それらの確率が排反事象であるかどうかで解法が変わってきます。ポイントはそれらが同時に起こりか起こらないかです!ベン図も有効ですので描けるようになりましょう。