約数の個数・平方数の解法
例えば、\(24\) の約数の個数は、\(24\) を素因数分解すると、$$~~~24=2^3\times 3^1$$となる。ここで、\(2^3\) の正の約数は、$$~~~1~,~2~,~2^2~,~2^3$$次に \(3^1\) の正の約数は、$$~~~1~,~3$$よって、表を作成すると、
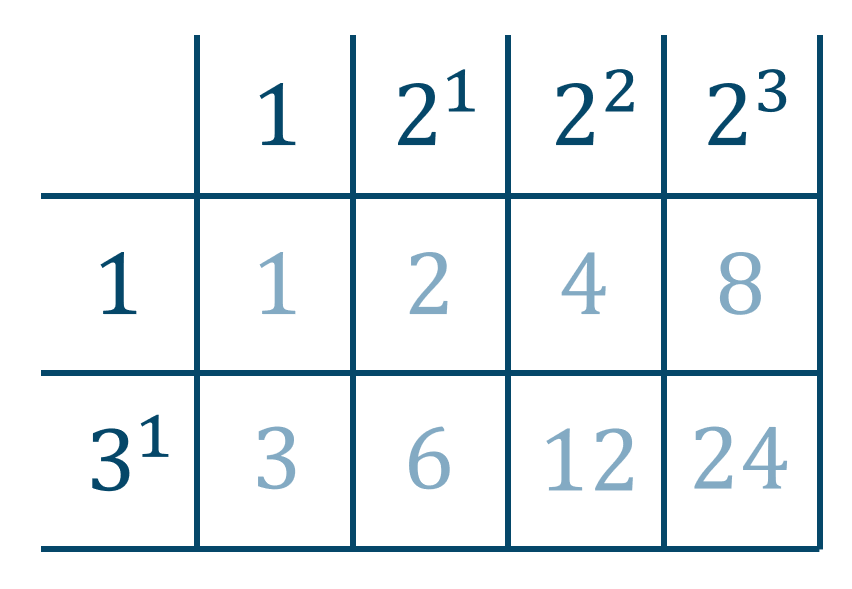
この表より、\(2^3\) の正の約数のおのおのに \(3^1\) の正の約数をかけると、\(24\) の約数となる。このことより、\(24\) の約数の個数は表のマスの数となるので、$$~~~4\times 2=8$$答えは \(8\) 個となります。
例えば \(\sqrt{24n}\) が自然数となるためには、\(\sqrt{(~~~)^2}\) のように、平方根の中が平方数となればよい。
① 平方根の中の自然数を素因数分解します。
② もとの数に代入して、平方根の外に出せる数は外に出しておきます。$$~~~~~~\sqrt{24n}$$$$~=\sqrt{2^3\times3\times n}$$$$~=2\sqrt{2\times3\times n}$$③ 平方根の中を考えて、平方数となるように \(n\) の値を定めます。$$~~~n=2\times3=6$$
問題解説:約数の個数・平方数
問題解説(1)
\({\small (1)}\) \(360\) の正の約数の個数を求めよ。
\(360\) を素因数分解すると、$$~~~360=2^3\times 3^2 \times 5^1$$よって、\(2^3\) の正の約数は、$$~~~1~,~2~,~2^2~,~2^3$$次に \(3^2\) の正の約数は、$$~~~1~,~3~,~3^2$$次に \(5^1\) の正の約数は、$$~~~1~,~5$$これより、\(2^3\) の正の約数のおのおのに \(3^2\) の正の約数をかけ、また、そのおのおのに \(5^1\) の正の約数をかけると \(360\) の約数になるので、$$~~~4\times 3 \times 2=24$$答えは \(24\) 個となります。
問題解説(2)
\({\small (2)}\) \(\sqrt{120n}\) が自然数となるような最小の自然数 \(n\) の値を求めよ。
\(120\) を素因数分解すると、$$~~~120=2^3\times3\times5$$よって、与式は$$~~~~~~\sqrt{120n}$$$$~=\sqrt{2^3\cdot3\cdot5\cdot n}$$$$~=2\sqrt{2\cdot3\cdot5\cdot n}$$これが自然数になるためには、平方根の中が平方数となればよいので、$$\hspace{ 10 pt}n=2\times3\times5=30$$よって、答えは$$~~~n=30$$となります。
今回のまとめ
約数の個数では素因数の組合せを考えましょう。また、平方根への応用問題は、平方根の中を平方数とするように計算していきましょう。



