不定方程式の利用
(1) 2つの数でそれぞれ割ったときの余り
(2) 桁数と最小(最大)の条件
これらが条件として与えられているとき、解法の手順は、
① (1)の条件より、この自然数 \(a\) を2通りの除法の式で表し、その式より不定方程式を立式します。
② 不定方程式を解き、この自然数 \(a\) を文字式で表します。
③ 求めた自然数 \(a\) の文字式と(2)の条件より値を定めます。
問題解説:不定方程式の利用
求める自然数を \(a\) とすると、
\(7\) で割ると \(3\) 余るので、$$~~~a=7x+3~~\cdots{\large ①}$$(ただし、\(x\) は整数)となります。
また、\(11\) で割ると \(6\) 余るので、$$~~~a=11y+6~~\cdots{\large ②}$$(ただし、\(y\) は整数)となります。
よって、①と②より$$\hspace{ 10 pt}7x+3=11y+6$$移項すると、$$\hspace{ 10 pt}7x-11y=6-3$$$$\hspace{ 10 pt}7x-11y=3~~\cdots{\large ③}$$ここで、③を満たす整数解の1つの組を調べると、
| \(\times1\) | \(7\) | \(11\) |
| \(\times2\) | \(14\) | \(22\) |
この表より、\(14-11=3\) であるから$$\hspace{ 10 pt}7\times2-11\times1=3~~\cdots{\large ④}$$ここで、③から④を両辺を引き算すると、$$\hspace{ 10 pt}7(x-2)-11(y-1)=3-3$$$$\hspace{ 10 pt}7(x-2)-11(y-1)=0$$移項すると、$$\hspace{ 10 pt}7(x-2)=11(y-1)$$\(x-2~,~y-1\) は整数で、\(7\) と \(11\) は互いに素であることより、\(x-2\) は \(11\) の倍数となります。$$~~~x-2=11m$$ただし \(m\) は整数となります。
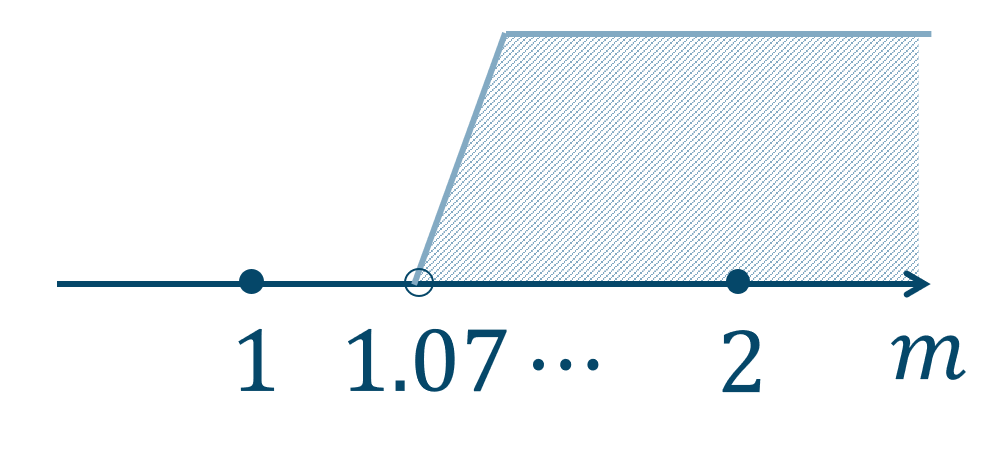
これより、$$\hspace{ 10 pt}x=11m+2~~\cdots{\large ⑤}$$これを①の式に代入すると、$$\hspace{ 10 pt}a=7x+3$$$$\hspace{ 18 pt}=7(11m+2)+3$$$$\hspace{ 18 pt}=77m+14+3$$$$\hspace{ 18 pt}=77m+17~~\cdots{\large ⑥}$$ここで、\(a\) は3桁の最小の整数であるので、\(100\) 以上の数となりことより、$$\hspace{ 10 pt}a=77m+17≧100$$移項して計算すると、$$\hspace{ 10 pt}77m≧100-17$$$$\hspace{ 10 pt}77m≧83$$両辺を \(77\) で割ると、$$\hspace{ 10 pt}m≧\frac{83}{77}=1.07\cdots$$数直線上に表すと、
これより、\(m=2\) のとき最小の整数となります。
⑥の式に代入すると、$$\hspace{ 10 pt}a=77\times2+17$$$$\hspace{ 18 pt}=154+17$$$$\hspace{ 18 pt}=171$$よって、求める自然数は \(171\) となります。
今回のまとめ
不定方程式の解法を利用することも重要ですが、桁数と最小(最大)の条件を用いて不等式の整数解を求める手順も覚えておきましょう。