内分点と外分点の位置
Point:内分点と外分点・内分点
線分 \({\rm AB}\) を \(m:n\) に内分する点 \({\rm P}\)

図のように \({\rm A}~\to~{\rm B}\) を \(m\) と \(n\) に分けて進んだと考えましょう。
・外分点
線分 \({\rm AB}\) を \(m:n\) に外分する点 \({\rm Q}\)
( ⅰ ) \(m>n\) のとき、
\({\rm A}~\to~{\rm B}\) を \(m\) 進んで \(n\) 戻ると考えて、

( ⅱ ) \(m<n\) のとき、
\({\rm A}~\to~{\rm B}\) を \(m\) 戻り \(n\) 進むと考えて、

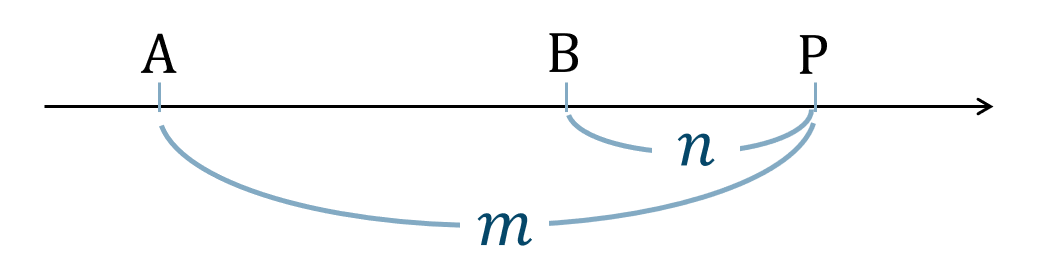
線分 \({\rm AB}\) を \(m:n\) に内分する点 \({\rm P}\)
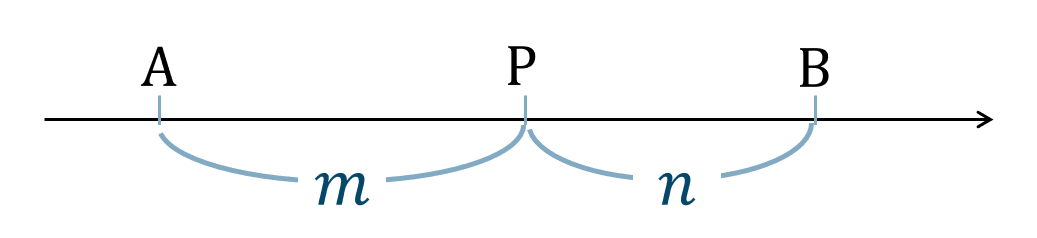
図のように \({\rm A}~\to~{\rm B}\) を \(m\) と \(n\) に分けて進んだと考えましょう。
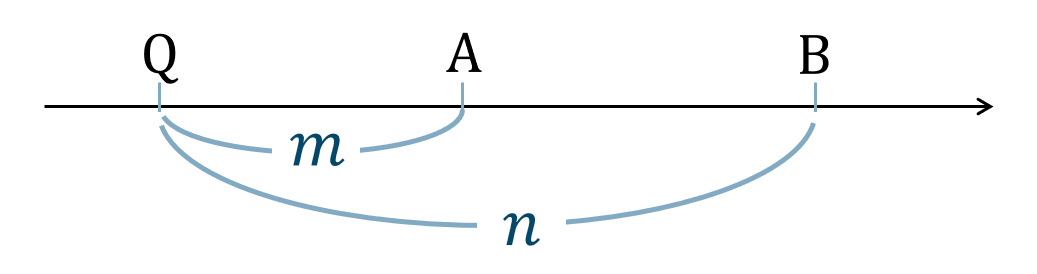
・外分点
線分 \({\rm AB}\) を \(m:n\) に外分する点 \({\rm Q}\)
( ⅰ ) \(m>n\) のとき、
\({\rm A}~\to~{\rm B}\) を \(m\) 進んで \(n\) 戻ると考えて、
( ⅱ ) \(m<n\) のとき、
\({\rm A}~\to~{\rm B}\) を \(m\) 戻り \(n\) 進むと考えて、
問題解説:内分点と外分点の位置
問題解説(1)
問題数直線上に次の点を図示せよ。
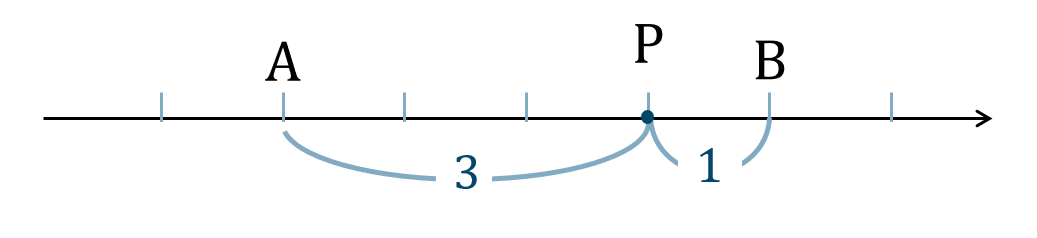
\({\small (1)}\) 線分 \({\rm AB}\) を \(3:1\) に内分する点 \({\rm P}\)
\({\small (1)}\) 線分 \({\rm AB}\) を \(3:1\) に内分する点 \({\rm P}\)
線分 \({\rm AB}\) を \(3:1\) に内分するので、
\({\rm A}~\to~{\rm B}\) を \(3\) と \(1\) に分けて進んだと考えて、
問題解説(2)
問題数直線上に次の点を図示せよ。
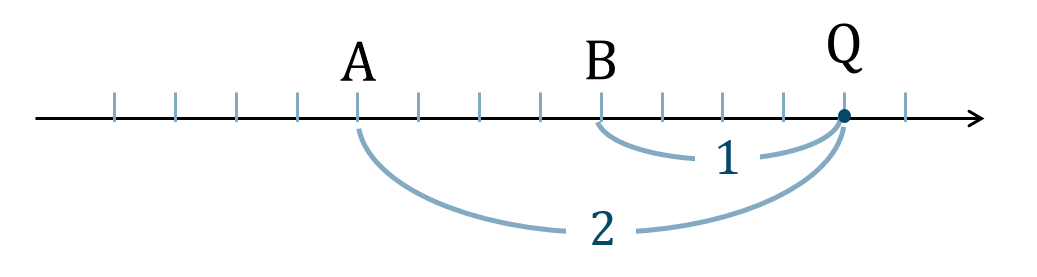
\({\small (2)}\) 線分 \({\rm AB}\) を \(2:1\) に外分する点 \({\rm Q}\)
\({\small (2)}\) 線分 \({\rm AB}\) を \(2:1\) に外分する点 \({\rm Q}\)
線分 \({\rm AB}\) を \(2:1\) に外分するので、
\({\rm A}~\to~{\rm B}\) を \(2\) 進んで \(1\) 戻ると考えて、
問題解説(3)
問題数直線上に次の点を図示せよ。
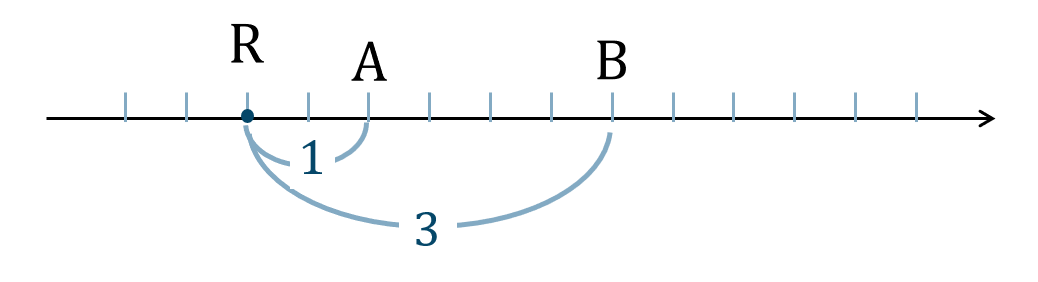
\({\small (3)}\) 線分 \({\rm AB}\) を \(1:3\) に外分する点 \({\rm R}\)
\({\small (3)}\) 線分 \({\rm AB}\) を \(1:3\) に外分する点 \({\rm R}\)
線分 \({\rm AB}\) を \(1:3\) に外分するので、
\({\rm A}~\to~{\rm B}\) を \(1\) 戻って \(3\) 進むと考えて、
今回のまとめ
内分点と外分点の位置は、線分の端から端までどのように進むかを考えて図示していきましょう。

【問題一覧】数学A:図形の性質
このページは「高校数学A:図形の性質」の問題一覧ページとなります。解説の見たい単元名がわからないとき...