円に内接する四角形と角
四角形の対角の和は \(180^\circ\) となります。
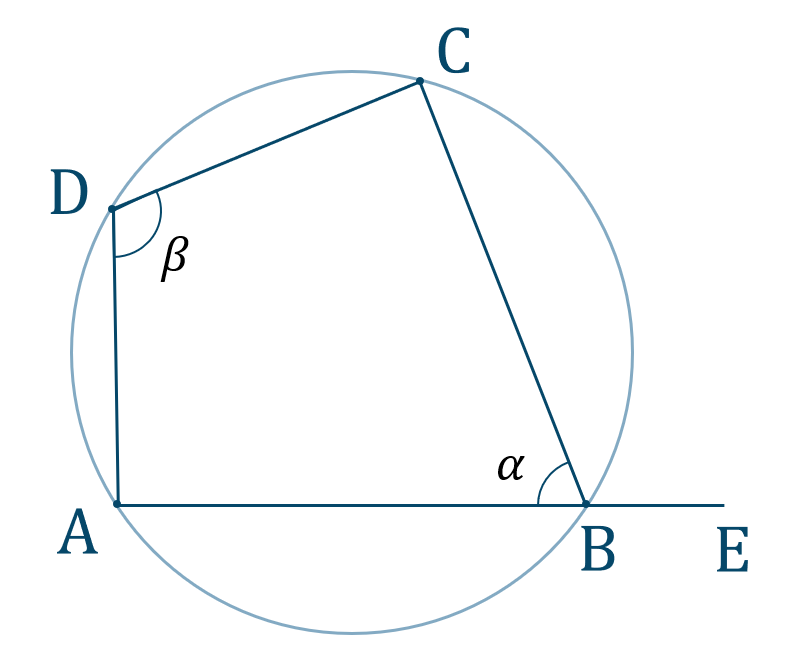
上の図より、
逆に、四角形の対角が等しければその四角形は円に内接します。
問題解説:円に内接する四角形と角
問題解説(1)
\({\small (1)}\) 次の図の角度 \(x~,~y\) の値を求めよ。
\({\large ①}\)
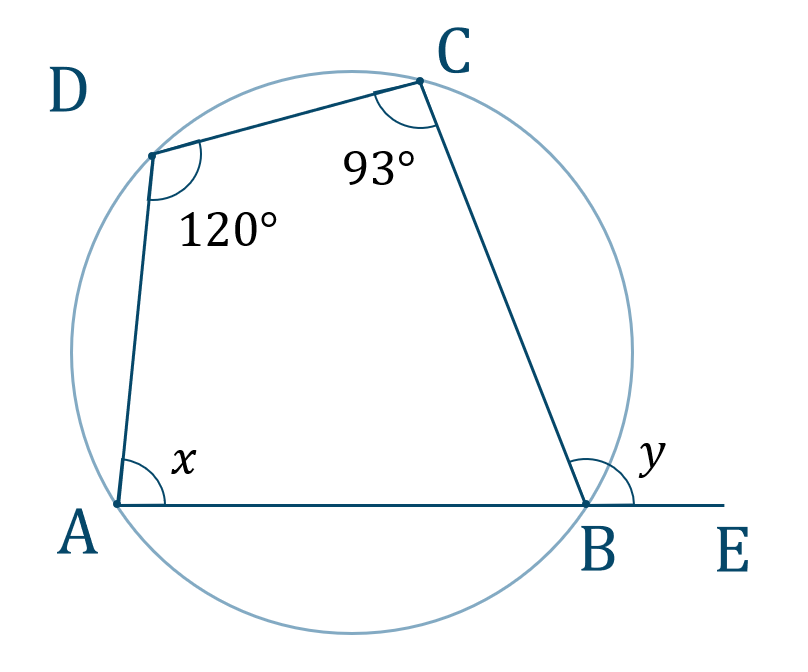
\({\large ②}\)
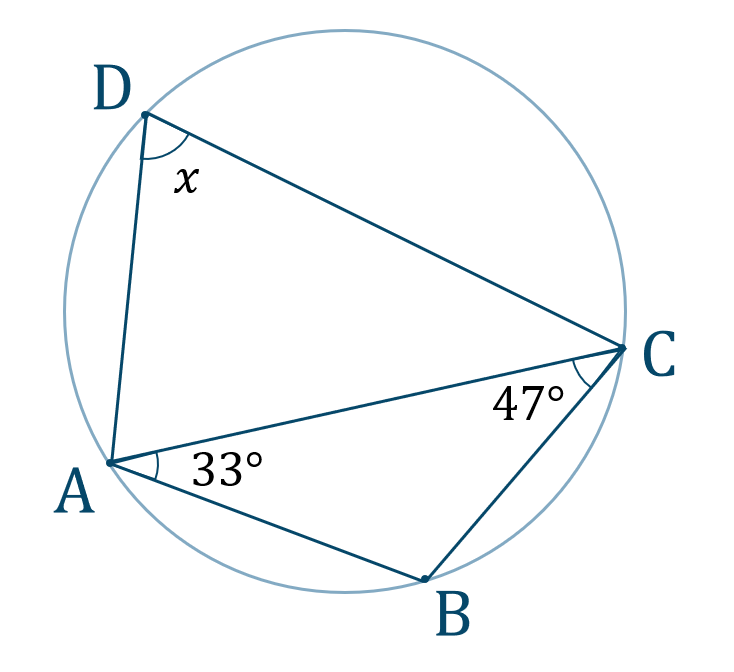


\({\large ①}\)

円に内接する四角形の条件より、$$~~~\angle{\rm DAB}+\angle{\rm DCB}=180^\circ$$よって、値を代入すると、$$\hspace{ 10 pt}x+93^\circ=180^\circ$$移項すると、$$\hspace{ 10 pt}x=180^\circ-93^\circ$$$$\hspace{ 19 pt}=87^\circ$$
次に、円に内接する四角形の条件より、$$~~~\angle{\rm ADC}+\angle{\rm ABC}=180^\circ$$値を代入すると、$$\hspace{ 10 pt}120^\circ+\angle{\rm ABC}=180^\circ$$移項すると、$$\hspace{ 10 pt}\angle{\rm ABC}=180^\circ-120^\circ$$$$\hspace{ 42 pt}=60^\circ$$
また、\(\angle{\rm ABC}+\angle{\rm CBE}=180^\circ\) より、$$\hspace{ 10 pt}60^\circ+y=180^\circ$$移項すると、$$\hspace{ 10 pt}y=180^\circ-60^\circ$$$$\hspace{ 18 pt}=120^\circ$$
よって、答えは$$~~~x=87^\circ~,~y=120^\circ$$となります。
\({\large ②}\)

図より、\(\triangle {\rm ABC}\) について内角の和より、$$\hspace{ 10 pt}\angle{\rm CAB}+\angle{\rm ABC}+\angle{\rm ACB}=180^\circ$$値を代入すると、$$\hspace{ 10 pt}33^\circ+\angle{\rm ABC}+47^\circ=180^\circ$$移項すると、$$\hspace{ 10 pt}\angle{\rm ABC}=180^\circ-(33^\circ+47^\circ)$$$$\hspace{ 42 pt}=180^\circ-80^\circ$$$$\hspace{ 42 pt}=100^\circ$$
次に、円に内接する四角形の条件より、$$~~~\angle{\rm ADC}+\angle{\rm ABC}=180^\circ$$値を代入すると、$$\hspace{ 10 pt}x+100^\circ=180^\circ$$移項すると、$$\hspace{ 10 pt}x=180^\circ-100^\circ$$$$\hspace{ 19 pt}=80^\circ$$
よって、答えは \(x=80^\circ\) となります。
問題解説(2)
\({\small (2)}\) 次の四角形の中で円に内接するものをすべて選べ。
\({\large ①}\)
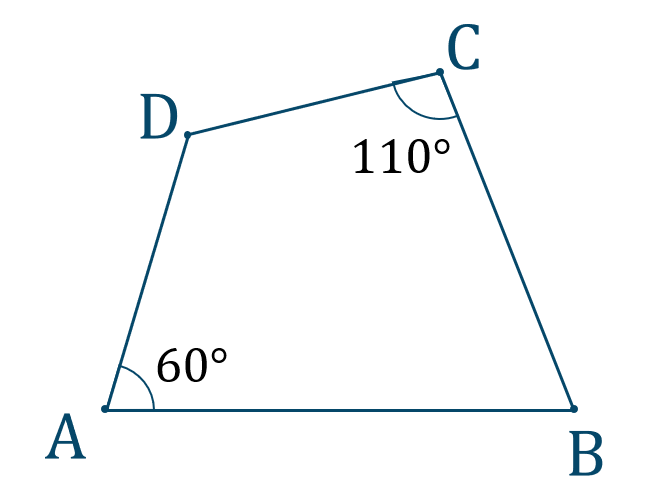


\({\large ②}\)



\({\large ③}\)


\({\large ①}\)

図より、四角形の対角の和は、$$~~~60^\circ+110^\circ=170^\circ$$よって、\(180^\circ\) とならないので、円に内接しません。
\({\large ②}\)

図より、\(\triangle {\rm ABD}\) の内角の和より、$$\hspace{ 10 pt}\angle{\rm DAB}+\angle{\rm ADB}+\angle{\rm ABD}=180^\circ$$値を代入すると、$$\hspace{ 10 pt}\angle{\rm DAB}+65^\circ+60^\circ=180^\circ$$移項すると、$$\hspace{ 10 pt}\angle{\rm DAB}=180^\circ-(65^\circ+60^\circ)$$$$\hspace{ 42 pt}=180^\circ-125^\circ$$$$\hspace{ 42 pt}=55^\circ$$
ここで、四角形の対角の和は、$$~~~55^\circ+125^\circ=180^\circ$$よって、\(180^\circ\) となるので、この四角形は円に内接します。
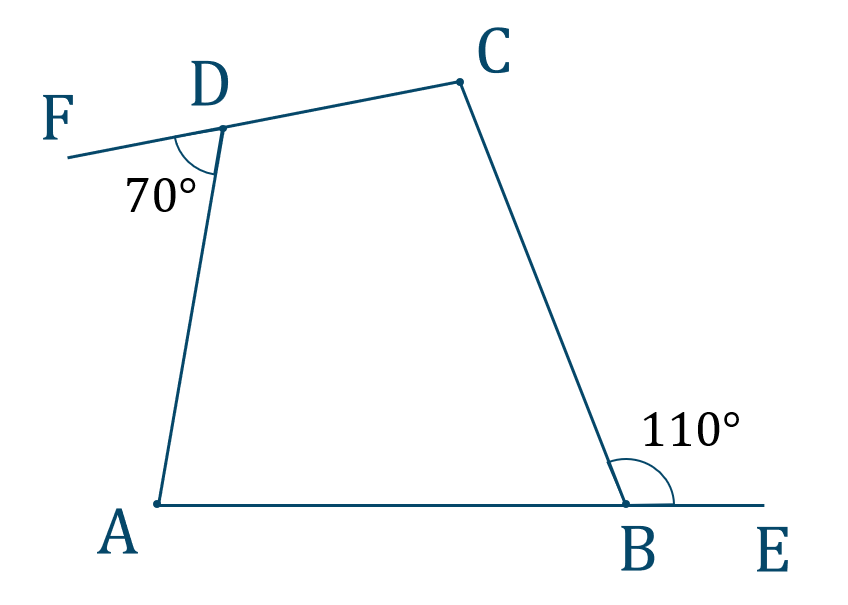
\({\large ③}\)

図より、点 \({\rm D}\) について、$$\hspace{ 10 pt}\angle{\rm FDA}+\angle{\rm ADC}=180^\circ$$値を代入すると、$$\hspace{ 10 pt}70^\circ+\angle{\rm ADC}=180^\circ$$移項すると、$$\hspace{ 10 pt}\angle{\rm ADC}=180^\circ-70^\circ$$$$\hspace{ 42 pt}=110^\circ$$
次に、点 \({\rm B}\) について、$$\hspace{ 10 pt}\angle{\rm ABC}+\angle{\rm CBE}=180^\circ$$値を代入すると、$$\hspace{ 10 pt}\angle{\rm ABC}+110^\circ=180^\circ$$移項すると、$$\hspace{ 10 pt}\angle{\rm ABC}=180^\circ-110^\circ$$$$\hspace{ 42 pt}=70^\circ$$
ここで、四角形の対角の和は、$$~~~110^\circ+70^\circ=180^\circ$$よって、\(180^\circ\) となるので、この四角形は円に内接します。
今回のまとめ
円に内接する四角形についての問題は、対角の和が \(180^\circ\) となることを用いて解いていきましょう。また、逆の場合も四角形の対角の和を調べましょう。




