接弦定理
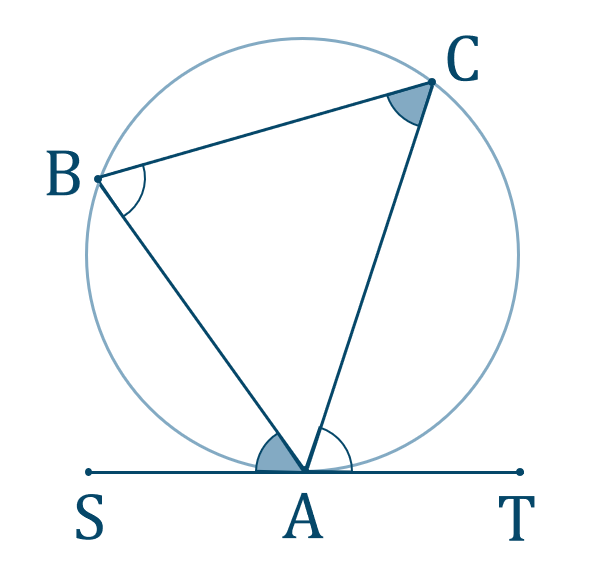
上の図で、\(\triangle {\rm ABC}\) の外接円と点 \({\rm A}\) での接線 \({\rm ST}\) において、
また、
これらが成り立ちます。
問題解説:接弦定理
問題解説(1)
\({\small (1)}\)
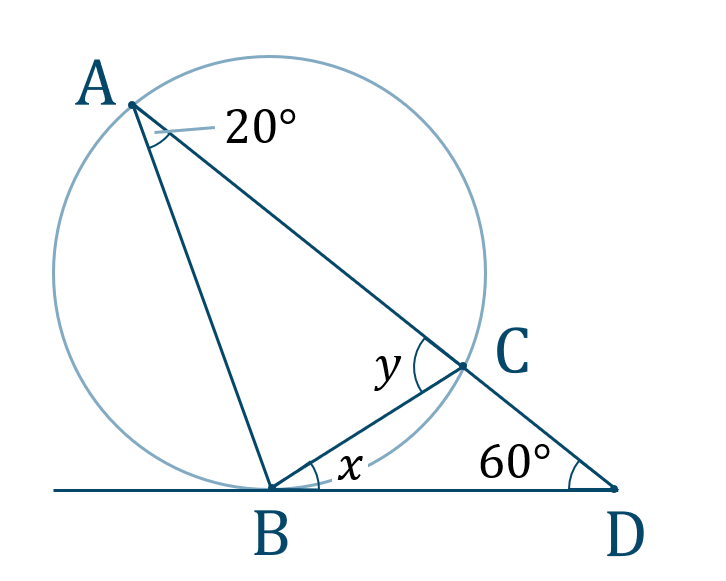
接弦定理より、$$\hspace{ 10 pt}\angle{\rm CBD}=\angle{\rm BAC}$$よって、値を代入すると、$$\hspace{ 10 pt}x=20^\circ$$
また、\(\triangle {\rm BCD}\) について、外角は他の2つの内角の和となるので、$$\hspace{ 10 pt}\angle{\rm ACB}=\angle{\rm CBD}+\angle{\rm CDB}$$よって、値を代入すると、$$\hspace{ 10 pt}y=20^\circ+60^\circ$$$$\hspace{ 18 pt}=80^\circ$$
よって、答えは$$~~~x=20^\circ~,~y=80^\circ$$となります。
問題解説(2)
\({\small (2)}\)

接弦定理より、$$\hspace{ 10 pt}\angle{\rm ACB}=\angle{\rm ABE}$$よって、値を代入すると、$$\hspace{ 10 pt}x=62^\circ$$
次に、円に内接する四角形の条件より、$$\hspace{ 10 pt}\angle{\rm ADC}+\angle{\rm ABC}=180^\circ$$よって、値を代入すると、$$\hspace{ 10 pt}107^\circ+\angle{\rm ABC}=180^\circ$$移項すると、$$\hspace{ 10 pt}\angle{\rm ABC}=180^\circ-107^\circ$$$$\hspace{ 43 pt}=73^\circ$$
また、\(\triangle {\rm ABC}\) の内角の和より、$$\hspace{ 10 pt}\angle{\rm BAC}+\angle{\rm ACB}+\angle{\rm ABC}=180^\circ$$値を代入すると、$$\hspace{ 10 pt}y+62^\circ+73^\circ=180^\circ$$移項すると、$$\hspace{ 10 pt}y=180^\circ-(62^\circ+73^\circ)$$$$\hspace{ 18 pt}=180^\circ-135^\circ$$$$\hspace{ 18 pt}=45^\circ$$
よって、答えは$$~~~x=62^\circ~,~y=45^\circ$$となります。
今回のまとめ
円とその接線がある角度の問題は、接弦定理を用いて考えるようにしましょう。また、他の三角形の性質や円に内接する四角形の性質なども同時に利用しましょう。



