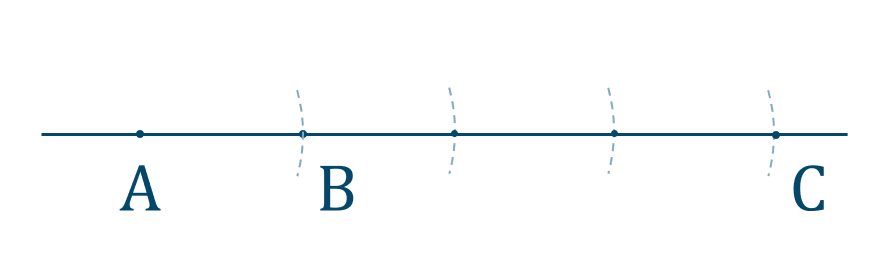問題解説：平方根の値の作図
問題長さ \(1\) が与えられたとき、長さ \(\sqrt{3}\) の作図をせよ。
長さ \(1\) の線分 \({\rm AB}\) 上に \({\rm BC}=3\) となるようにコンパスを用いて点 \({\rm C}\) をとります。
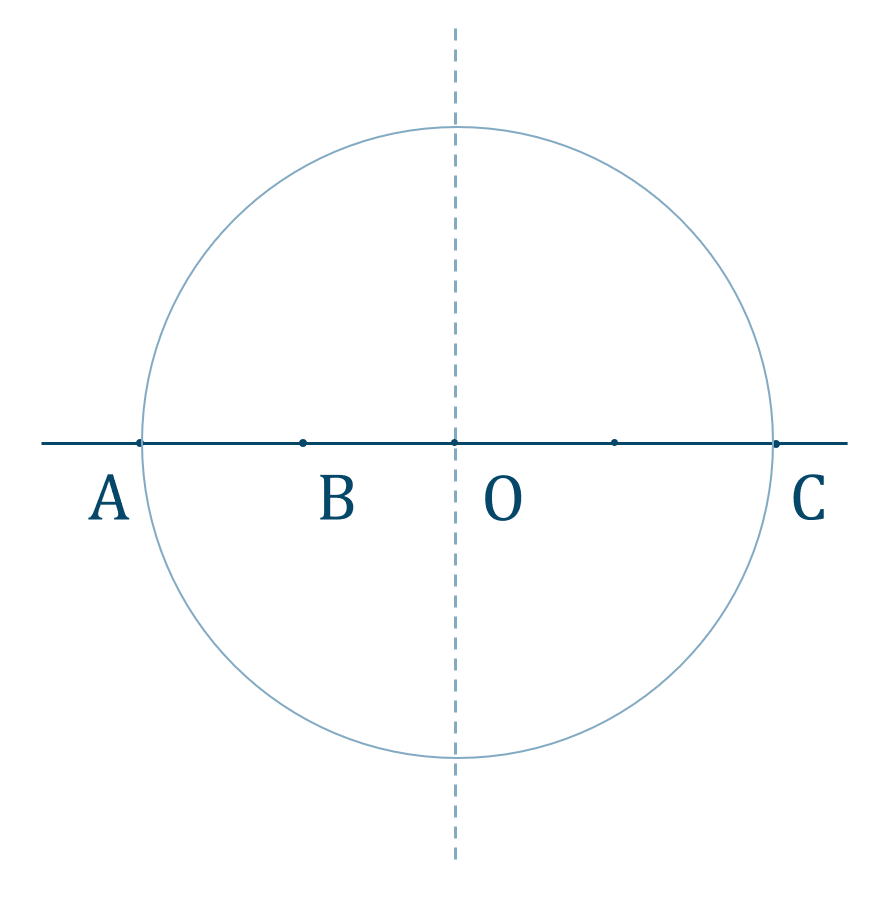
線分 \({\rm AC}\) の垂直二等分線を作図して、\({\rm AC}\) を直径とする円を作図します。
（今回の問題では、\({\rm BC}\) を３等分した１つ目の点が円の中心となります。）
この垂直二等分線に平行で点 \({\rm B}\) を通る直線を作図します。
（点 \({\rm B}\) を通り、直線 \({\rm AC}\) に垂直な直線を作図しても同じになります。）
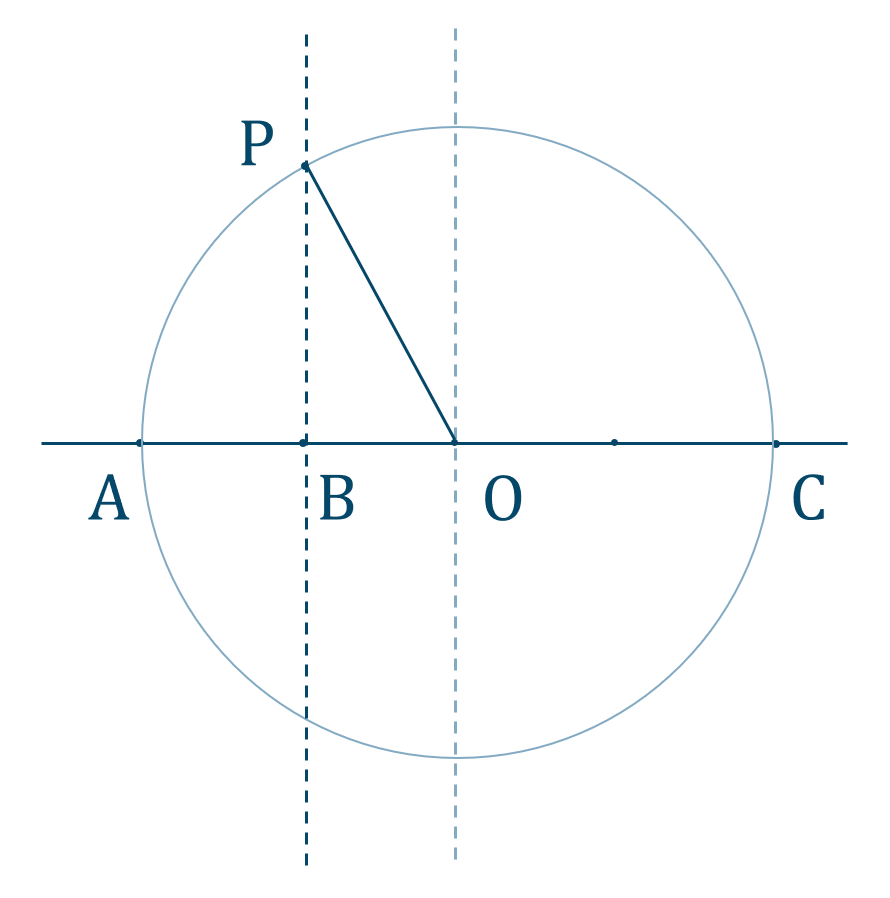
このとき、円との交点を \({\rm P}\) とすると、$$~~~{\rm BP}=\sqrt{3}$$となります。
今回のまとめ
平方根の長さの作図でも、平方根の中の値を用いて作図していく方法を覚えておきましょう。
【問題一覧】数学Ａ：図形の性質
このページは「高校数学Ａ：図形の性質」の問題一覧ページとなります。解説の見たい単元名がわからないとき...
yorikuwa.com
