問題解説:空間図形の位置関係
問題解説(1)
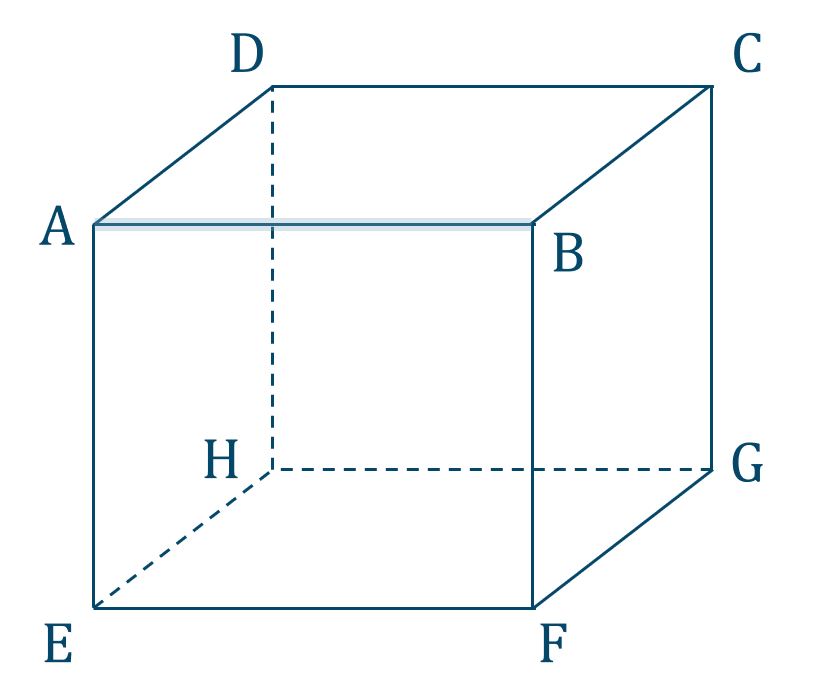
\({\small (1)}\) 線分 \({\rm AB}\) に平行な辺
図より平行となるのは、
辺 \({\rm DC}\) \(,\) \({\rm EF}\) \(,\) \({\rm HG}\)
となります。
問題解説(2)
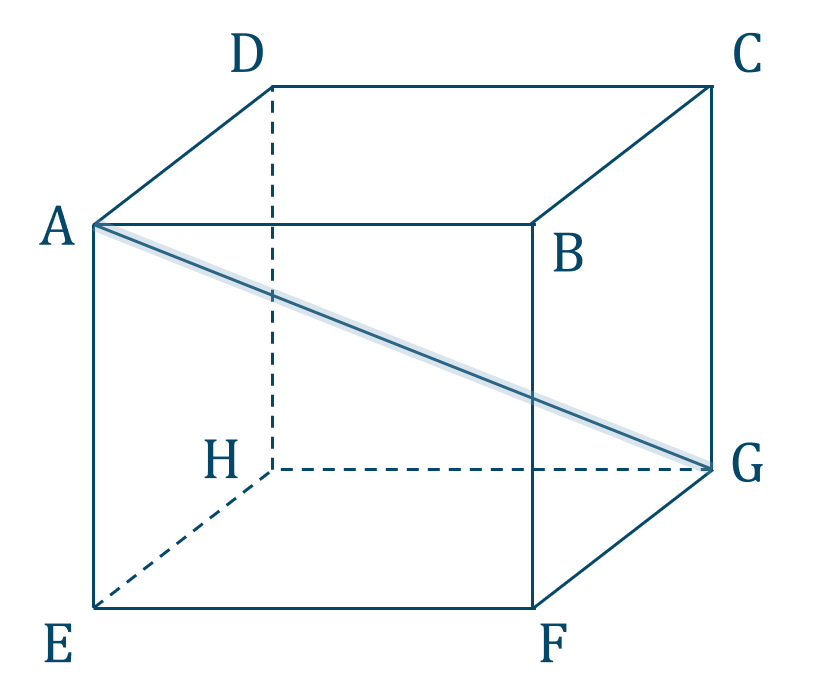
図より、点 \({\rm A}\) で線分 \({\rm AG}\) と交わる辺 \({\rm AB}\) \(,\) \({\rm AD}\) \(,\) \({\rm AE}\) はねじれの位置ではない。
点 \({\rm G}\) で線分 \({\rm AG}\) と交わる辺 \({\rm GC}\) \(,\) \({\rm GF}\) \(,\) \({\rm GH}\) はねじれの位置ではない。
次に、辺 \({\rm BC}\) \(,\) \({\rm DC}\) \(,\) \({\rm BF}\) \(,\) \({\rm EF}\) \(,\) \({\rm EH}\) \(,\) \({\rm DH}\) はその延長線も直線 \({\rm AB}\) と交わらないのでねじれの位置となります。
よって、答えは
辺 \({\rm BC}\) \(,\) \({\rm DC}\) \(,\) \({\rm BF}\) \(,\) \({\rm EF}\) \(,\) \({\rm EH}\) \(,\) \({\rm DH}\)
となります。
問題解説(3)
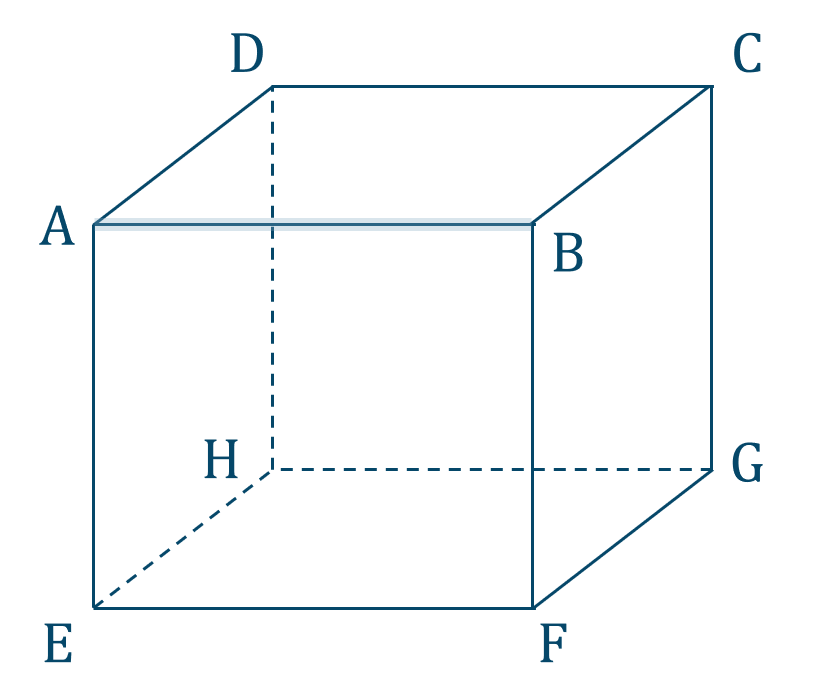
図より、点 \({\rm A}\) で垂直となる辺は、
辺 \({\rm AD}\) \(,\) \({\rm AE}\)
また、点 \({\rm B}\) で垂直となる辺は、
辺 \({\rm BC}\) \(,\) \({\rm BF}\)
次に、線分 \({\rm AB}\) で垂直な面は、
点 \({\rm A}\) で垂直な面 \({\rm AEHD}\)
点 \({\rm B}\) で垂直な面 \({\rm BFGC}\)
ここで、面 \({\rm ABFE}\) や面 \({\rm ABCD}\) は線分 \({\rm AB}\) を含む面なので、垂直にはならない。
よって、答えは
辺 \({\rm AD}\) \(,\) \({\rm AE}\) \(,\) \({\rm BC}\) \(,\) \({\rm BF}\)
面 \({\rm AEHD}\) \(,\) \({\rm BFGC}\)
となります。
問題解説(4)
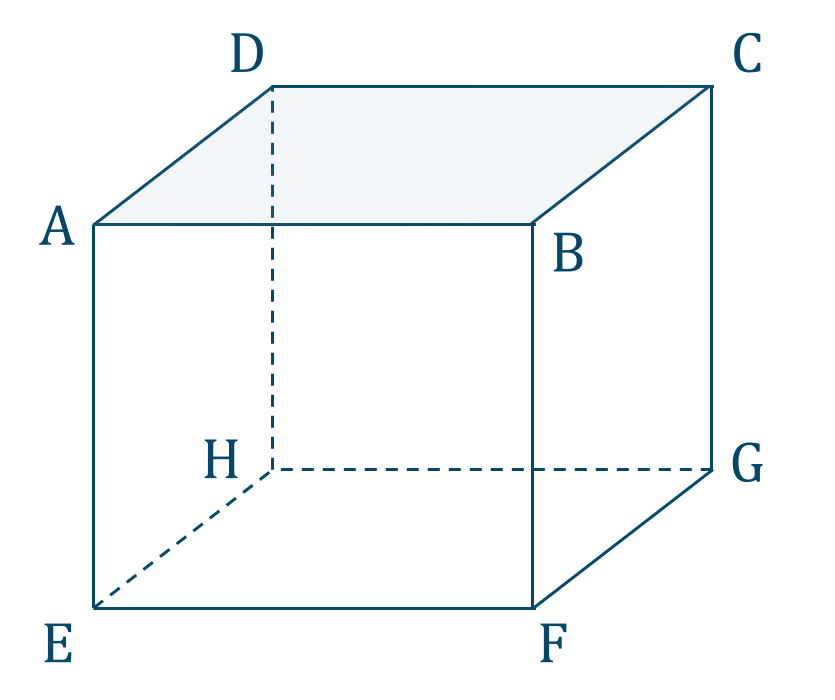
図より、平行な辺や面は
線分 \({\rm AB}\) や \({\rm DC}\) と平行な辺の
辺 \({\rm EF}\) \(,\) \({\rm GH}\)
線分 \({\rm AD}\) や \({\rm BC}\) と平行な辺の
辺 \({\rm EH}\) \(,\) \({\rm FG}\)
面 \({\rm ABCD}\) に平行な面の
面 \({\rm EFGH}\)
よって、答えは
辺 \({\rm EF}\) \(,\) \({\rm GH}\) \(,\) \({\rm EH}\) \(,\) \({\rm FG}\)
面 \({\rm EFGH}\)
となります。
今回のまとめ
空間図形の位置は、対象となる辺や面を図形に描き視覚的に判断していきましょう。また、ねじれの位置はすべての辺とその延長線上も調べるようにしましょう。