等しいベクトルと逆ベクトル
で表します。
また、\(\overrightarrow{a}\) に対して、
「大きさが等しく、向きが反対であるベクトル」
を逆ベクトルといい、
で表します。
問題解説:ベクトルの基本
問題解説(1)
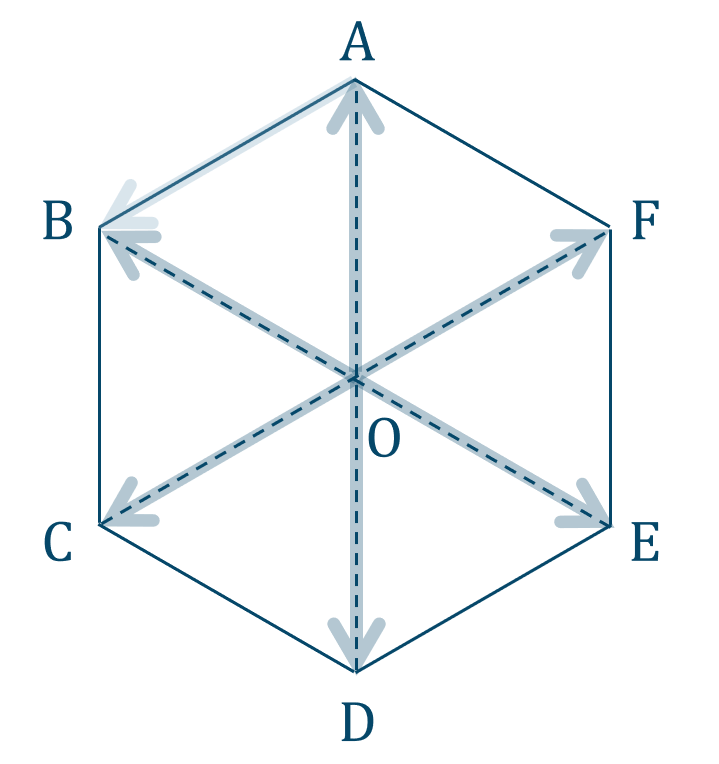
\({\small (1)}\) \(\overrightarrow{\rm AB}\) と大きさが等しく始点が \({\rm O}\) のベクトル。
長さが \(\overrightarrow{\rm AB}\) と同じで始点が \({\rm O}\) のベクトルとなるので、
図より、答えは$$~~~\overrightarrow{\rm OA}~,~ \overrightarrow{\rm OB}~,~ \overrightarrow{\rm OC}~,~ \overrightarrow{\rm OD}~,~ \overrightarrow{\rm OE}~,~ \overrightarrow{\rm OF}$$となります。
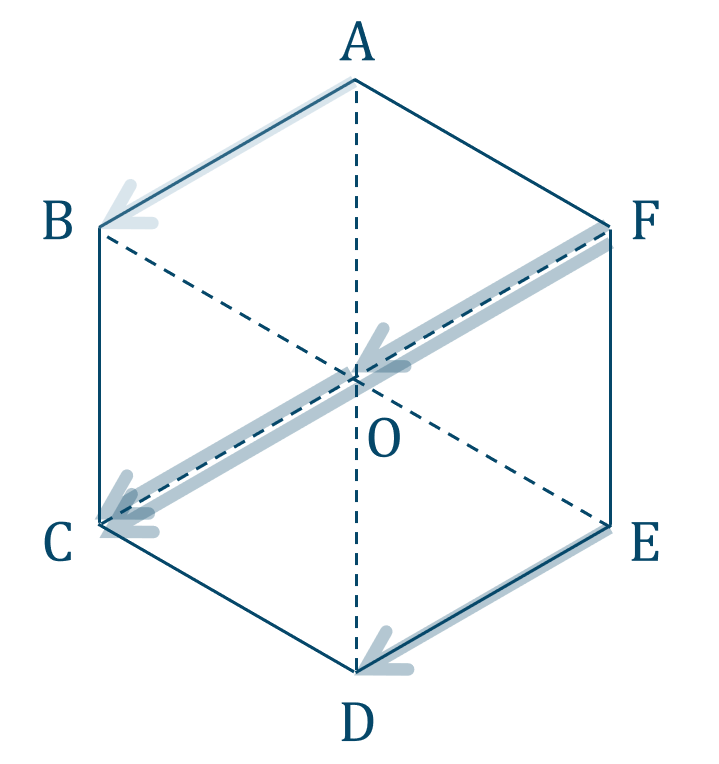
問題解説(2)
向きが同じベクトルは平行移動して重なればよいので、
図より、直線 \({\rm CF}\) 上では、$$~~~\overrightarrow{\rm FO}~,~ \overrightarrow{\rm OC}~,~ \overrightarrow{\rm FC}$$直線 \({\rm DE}\) 上では、$$~~~\overrightarrow{\rm ED}$$
よって、答えは$$~~~\overrightarrow{\rm FO}~,~ \overrightarrow{\rm OC}~,~ \overrightarrow{\rm FC}~,~\overrightarrow{\rm ED}$$となります。
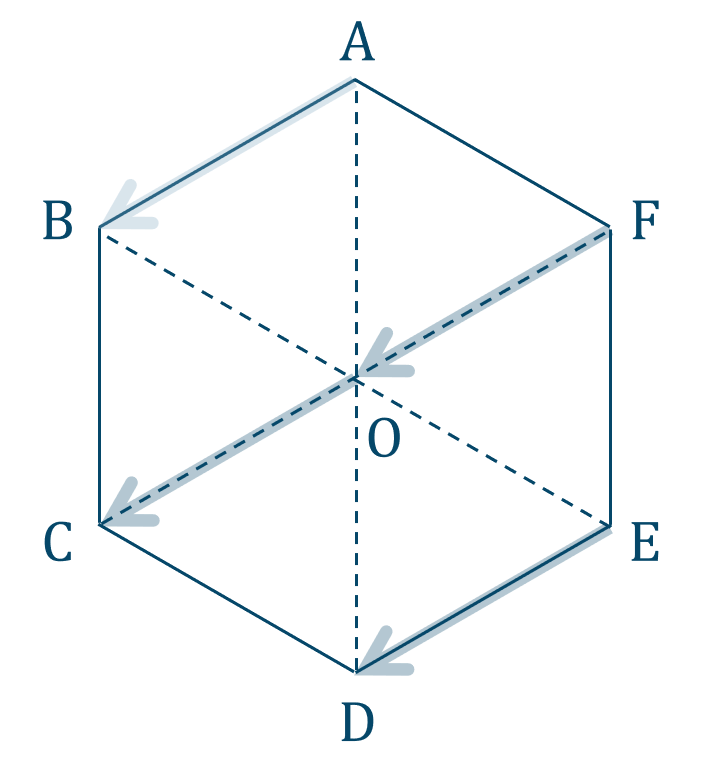
問題解説(3)
等しいベクトルは
「向きが同じで大きさが等しくベクトル」
であるので、
図より答えは$$~~~\overrightarrow{\rm FO}~,~ \overrightarrow{\rm OC}~,~ \overrightarrow{\rm ED}$$となります。
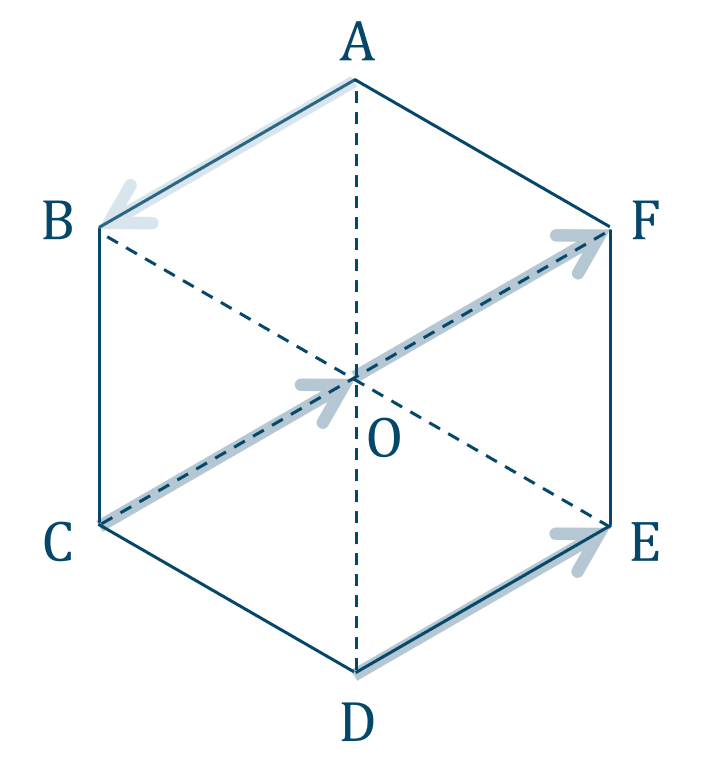
問題解説(4)
逆ベクトルは、
「大きさが等しく、向きが反対のベクトル」
であるので、
図より、答えは$$~~~\overrightarrow{\rm BA}~,~ \overrightarrow{\rm CO}~,~ \overrightarrow{\rm OF}~,~\overrightarrow{\rm DE}$$となります。
今回のまとめ
等しいベクトルは2つの条件について覚えておきましょう。また、逆ベクトルについてもおさえておきましょう。