ベクトルと三角形の面積
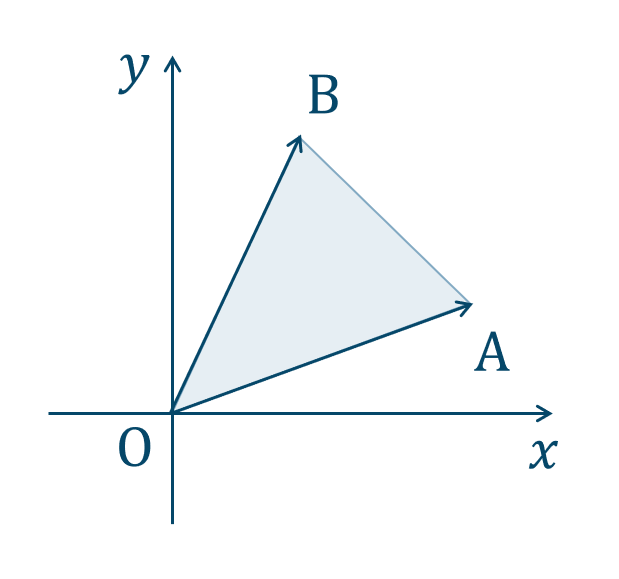
2つのベクトル \(\overrightarrow{\rm OA}\) と \(\overrightarrow{\rm OB}\) のそれぞれの大きさ \(|\overrightarrow{\rm OA}|\) と \(|\overrightarrow{\rm OB}|\) と、これらの内積を \(\overrightarrow{\rm OA}\cdot\overrightarrow{\rm OB}\) とするとき、
この三角形の面積 \(S\) は、
また、2つのベクトル \(\overrightarrow{\rm OA}~,~\overrightarrow{\rm OB}\) の成分が、$$~~~\overrightarrow{\rm OA}=\left(\begin{array} {c} x_a \\ y_a \end{array}\right)~,~\overrightarrow{\rm OB}=\left(\begin{array} {c} x_b \\ y_b \end{array}\right)$$のとき、この三角形の面積 \(S\) は、
となります。
問題解説:ベクトルと三角形の面積
問題解説(1)
\({\small (1)}\) 3点 \({\rm O~,~A~,~B}\) について、\(|\overrightarrow{\rm OA}|=4\) \(,\) \(|\overrightarrow{\rm OB}|=\sqrt{5}\) \(,\) \(\overrightarrow{\rm OA}\cdot\overrightarrow{\rm OB}=2\sqrt{5}\) のとき、 \(\triangle {\rm OAB}\) の面積を求めよ。
\(\triangle {\rm OAB}\) の面積を \(S\) とすると、$$~~~S=\frac{1}{2}\sqrt{|\overrightarrow{\rm OA}|^2|\overrightarrow{\rm OB}|^2-(\overrightarrow{\rm OA}\cdot\overrightarrow{\rm OB})^2}$$よって、値を代入すると、$$~~~~~~\frac{1}{2}\sqrt{4^2\cdot(\sqrt{5})^2-(2\sqrt{5})^2}$$$$~=\frac{1}{2}\sqrt{16\cdot5-20}$$$$~=\frac{1}{2}\sqrt{80-20}$$$$~=\frac{1}{2}\sqrt{60}$$$$~=\frac{1}{2}\cdot2\sqrt{15}$$$$~=\sqrt{15}$$
よって、答えは \(\sqrt{15}\) となります。
問題解説(2)
\(\triangle {\rm OAB}\) の面積を \(S\) とすると、2つのベクトルの成分は、$$~~~\overrightarrow{\rm OA}=\left(\begin{array} {c} 3 \\ 4 \end{array}\right)~,~\overrightarrow{\rm OB}=\left(\begin{array} {c} 2 \\ -1 \end{array}\right)$$であることより、面積 \(S\) は、$$~~~~~~S$$$$~=\frac{1}{2}|3\cdot(-1)-4\cdot2|$$$$~=\frac{1}{2}|-3-8|$$$$~=\frac{1}{2}|-11|$$$$~=\frac{11}{2}$$
よって、答えは$$~~~\frac{11}{2}$$となります。
今回のまとめ
ベクトルを用いた三角形の面積は、公式をしっかりと覚えておきましょう。また、成分が条件のときは頂点の1つが原点 \({\rm O}\) であることに注意しましょう。



